沪科版七年级上册 1.1正数和负数课件(共25张PPT)
文档属性
| 名称 | 沪科版七年级上册 1.1正数和负数课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 181.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-07 16:18:28 | ||
图片预览








文档简介
(共25张PPT)
第1章 有理数
1.1 正数和负数
小学数学里已学过了哪些数
情境导入
请同学们举几个具有相反意义的量.
你能用小学学过的数表示这些量吗
一般地,对于具有相反意义的量,我们可把其中一种意义的量规定为正的,用过去学过的数(零除外)表示;
把与它意义相反的量规定为负的,用过去学过的数(零除外)前面放上一个“ ”(读作“负”)号来表示。
新知构建
注:正负是相对的
1、汽车向东行驶3千米和向西行驶2千米
2、温度是零上10℃ 和零下5 ℃
3、收入500元和支出237元
4、水位升高1.2米和下降0.7米
5、买进100辆自行车和卖出20辆自行车
为了表示具有相反意义的量,上面我们引进了-5、-2、-237、-0.7等数,像这样的数是一种新数,叫做负数.
过去学过的那些数(零除外),如10、3、500、1.2等,叫做正数.正数前面有时也可以放上一个“+”(读作“正”)号,如10可以写成+10。
注意:零既不是正数,也不是负数
例1、填空:
(1)出口货物500吨记作-500,进口货物262吨记作______;
(2)如果产量增加20%,记作______,那么产量减少3%记作______;
(3)向东前进30m记作+30,向西前进10m记作______;
+262
+20%
-3%
-10
例题讲解
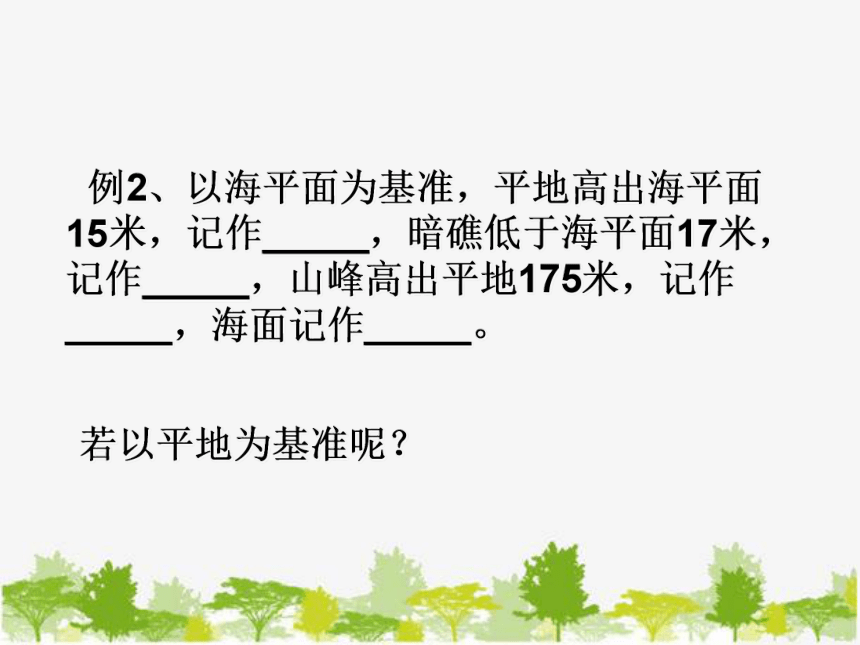
例2、以海平面为基准,平地高出海平面15米,记作_____,暗礁低于海平面17米,记作_____,山峰高出平地175米,记作_____,海面记作_____。
若以平地为基准呢?
例3、把下列叙述改成使用正数的方法
(1)向南走-20m,即_________;
(2)飞机下降-200米,即_________;
(3)飞机上升-3000米,即_________;
(4)商店赢利-1000元,即_________。
1.填空
(1)小东走5米记+5米,那么向西走6米记作______.
(2)获利200元记作+200元,亏损100元记作_____.
(3)前进10步记作______,后退5步记作______ .
(4)上升10米记作+10,那么-5表示______.
(5)向东记作正,则-12米的意思是______ .
(6) 海面下-200米相当于____________.
随堂练习
2.一潜水艇所在高度是-50m,一条鲨鱼在艇上方10m处,鲨鱼所在的高度是多少?
3.A地在某城东200米处,B地在A地西50米处,C地在B地东280米处,D地在B地西160米处。请规定某地为0,用有理数分别表示A、B、C、D的位置(单位:米 ),并求A到C、D的距离。
4.不用负数说明下面一些话的意义:
(1)向北走-50米
(2)气温下降-5C°
(3)运进-2000千克大米
(4)成本增加-5%
1.具有相反意义的量。
2.正数就是我们过去学过的数(0除外),在正数前面放上“-”号, 就是负数。
3.0既不是正数也不是负数。
归纳小结
正整数 :
零 :
负整数 :
正分数 :
负分数 :
新知构建
定义: 1、正整数、0、负整数统称整数, 正分数和负分数统称分数。 2、整数和分数统称有理数。
你能对以上各种数作出一张分类表吗?
按整数和分数分:
试一试
按性质(正数、负数)分:
有理数的两种分类,标准不同,所以结果也不同,需注意的是无论依据什么标准进行分类,分类时都要做到不重复不遗漏。
以下是两位同学的分类方法,你认为他们分类的结果正确吗?为什么?
(错)
(错)
定义:
把一些数放在一起,就组成一个数的集合,简称数集。
所有的有理数组成的数集叫做有理数集.类似地,所有的整数组成的数集叫做整数集,所有的正数组成的数集叫做正数集,所有的负数组成的数集叫做负数集,如此等等.
一.判断题(正确的打 “√”, 错误的打“×”)
(1)0是正整数;( )
(2)非负整数包含0;( )
(3)正分数一定是正有理数;( )
(4)有理数中没有最大的数;( )
×
√
√
√
随堂练习
二.选择题:
1、零不是( )。
A、非负数 B、有理数 C、正数 D、整数
2、下列说法错误的是( )。
A、-0.5是分数 B、0不是正数也不是负数 C、-2.74是负分数 D、非负数就是正数
C
D
3.下列说法中,正确的是( )。
A、正整数、负整数统称为整数
B、正分数、负分数统称为分数
C、零既可以是正整数,也可以是负整数
D、一个有理数不是正数就是负数
B
三. 把下面A、B、C、各表示一组数,把这些数填在圆圈中相应位置里。
A:{2, -4, 25, -3, -7, -12}
B:{-10 , -2 , -4 , 3 , 2, 10}
C:{-23 , -4 , -2 , 0 , 4 , 13}
A
C
B
1.表示全校每班出席人数的集合里的数都可能是什么样的有理数? 2.表示两队球赛胜负次数的集合里的数都可能是什么样的有理数? 3.A是由小于5的非负整数所组成的集合。B是由大于-3的非正整数所组成的集合。在A和B中有无相同的数?
能力拓展
1、有理数按正、负数,应怎样分类?
2、有理数按整数、分数,应怎样分类?
3、分类的原则是什么?
归纳小结
第1章 有理数
1.1 正数和负数
小学数学里已学过了哪些数
情境导入
请同学们举几个具有相反意义的量.
你能用小学学过的数表示这些量吗
一般地,对于具有相反意义的量,我们可把其中一种意义的量规定为正的,用过去学过的数(零除外)表示;
把与它意义相反的量规定为负的,用过去学过的数(零除外)前面放上一个“ ”(读作“负”)号来表示。
新知构建
注:正负是相对的
1、汽车向东行驶3千米和向西行驶2千米
2、温度是零上10℃ 和零下5 ℃
3、收入500元和支出237元
4、水位升高1.2米和下降0.7米
5、买进100辆自行车和卖出20辆自行车
为了表示具有相反意义的量,上面我们引进了-5、-2、-237、-0.7等数,像这样的数是一种新数,叫做负数.
过去学过的那些数(零除外),如10、3、500、1.2等,叫做正数.正数前面有时也可以放上一个“+”(读作“正”)号,如10可以写成+10。
注意:零既不是正数,也不是负数
例1、填空:
(1)出口货物500吨记作-500,进口货物262吨记作______;
(2)如果产量增加20%,记作______,那么产量减少3%记作______;
(3)向东前进30m记作+30,向西前进10m记作______;
+262
+20%
-3%
-10
例题讲解
例2、以海平面为基准,平地高出海平面15米,记作_____,暗礁低于海平面17米,记作_____,山峰高出平地175米,记作_____,海面记作_____。
若以平地为基准呢?
例3、把下列叙述改成使用正数的方法
(1)向南走-20m,即_________;
(2)飞机下降-200米,即_________;
(3)飞机上升-3000米,即_________;
(4)商店赢利-1000元,即_________。
1.填空
(1)小东走5米记+5米,那么向西走6米记作______.
(2)获利200元记作+200元,亏损100元记作_____.
(3)前进10步记作______,后退5步记作______ .
(4)上升10米记作+10,那么-5表示______.
(5)向东记作正,则-12米的意思是______ .
(6) 海面下-200米相当于____________.
随堂练习
2.一潜水艇所在高度是-50m,一条鲨鱼在艇上方10m处,鲨鱼所在的高度是多少?
3.A地在某城东200米处,B地在A地西50米处,C地在B地东280米处,D地在B地西160米处。请规定某地为0,用有理数分别表示A、B、C、D的位置(单位:米 ),并求A到C、D的距离。
4.不用负数说明下面一些话的意义:
(1)向北走-50米
(2)气温下降-5C°
(3)运进-2000千克大米
(4)成本增加-5%
1.具有相反意义的量。
2.正数就是我们过去学过的数(0除外),在正数前面放上“-”号, 就是负数。
3.0既不是正数也不是负数。
归纳小结
正整数 :
零 :
负整数 :
正分数 :
负分数 :
新知构建
定义: 1、正整数、0、负整数统称整数, 正分数和负分数统称分数。 2、整数和分数统称有理数。
你能对以上各种数作出一张分类表吗?
按整数和分数分:
试一试
按性质(正数、负数)分:
有理数的两种分类,标准不同,所以结果也不同,需注意的是无论依据什么标准进行分类,分类时都要做到不重复不遗漏。
以下是两位同学的分类方法,你认为他们分类的结果正确吗?为什么?
(错)
(错)
定义:
把一些数放在一起,就组成一个数的集合,简称数集。
所有的有理数组成的数集叫做有理数集.类似地,所有的整数组成的数集叫做整数集,所有的正数组成的数集叫做正数集,所有的负数组成的数集叫做负数集,如此等等.
一.判断题(正确的打 “√”, 错误的打“×”)
(1)0是正整数;( )
(2)非负整数包含0;( )
(3)正分数一定是正有理数;( )
(4)有理数中没有最大的数;( )
×
√
√
√
随堂练习
二.选择题:
1、零不是( )。
A、非负数 B、有理数 C、正数 D、整数
2、下列说法错误的是( )。
A、-0.5是分数 B、0不是正数也不是负数 C、-2.74是负分数 D、非负数就是正数
C
D
3.下列说法中,正确的是( )。
A、正整数、负整数统称为整数
B、正分数、负分数统称为分数
C、零既可以是正整数,也可以是负整数
D、一个有理数不是正数就是负数
B
三. 把下面A、B、C、各表示一组数,把这些数填在圆圈中相应位置里。
A:{2, -4, 25, -3, -7, -12}
B:{-10 , -2 , -4 , 3 , 2, 10}
C:{-23 , -4 , -2 , 0 , 4 , 13}
A
C
B
1.表示全校每班出席人数的集合里的数都可能是什么样的有理数? 2.表示两队球赛胜负次数的集合里的数都可能是什么样的有理数? 3.A是由小于5的非负整数所组成的集合。B是由大于-3的非正整数所组成的集合。在A和B中有无相同的数?
能力拓展
1、有理数按正、负数,应怎样分类?
2、有理数按整数、分数,应怎样分类?
3、分类的原则是什么?
归纳小结
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
