正弦定理[下学期]
图片预览





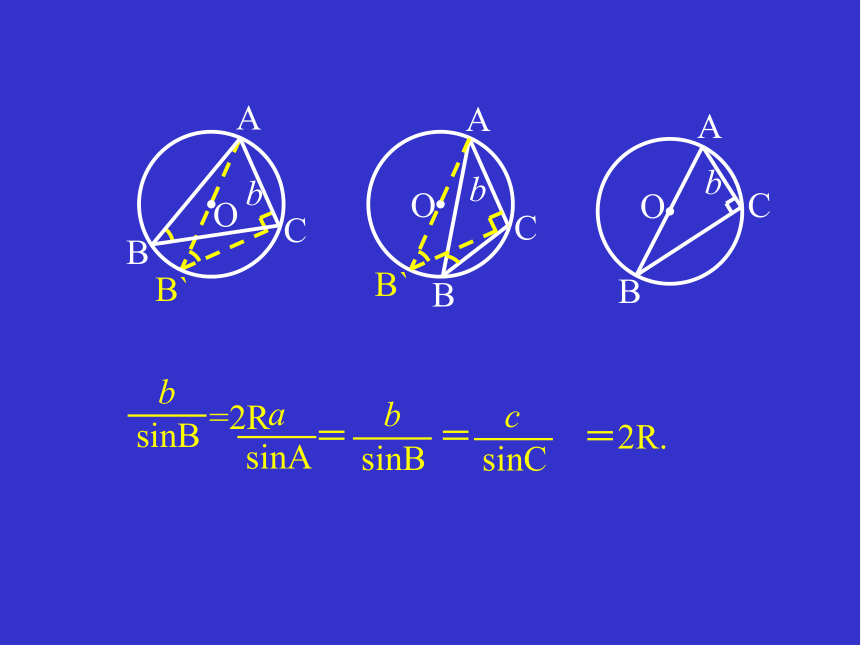
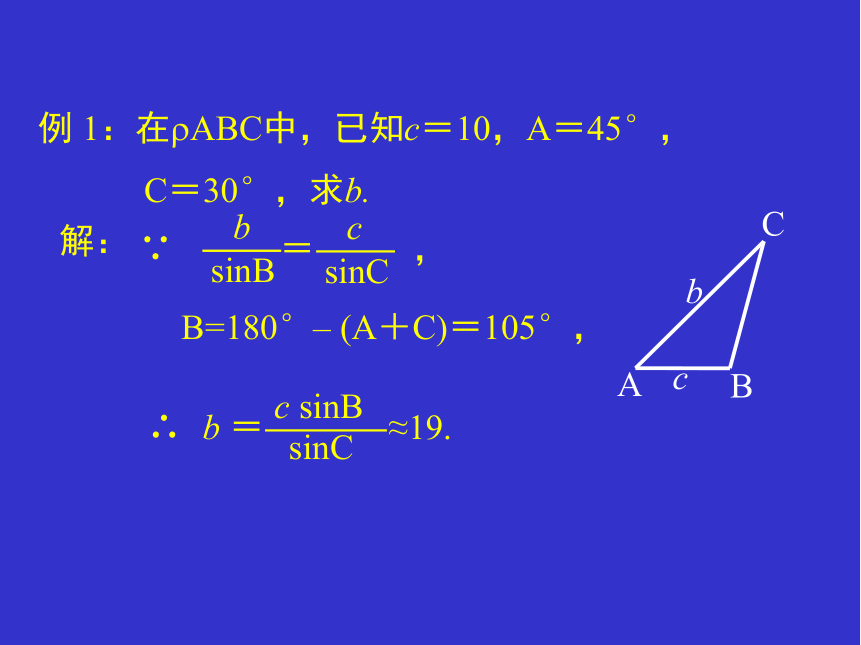
文档简介
(共18张PPT)
高一 数学
课题: 正弦定理
授课人:肖俊妮
怎样解直角三角形?
已知两边;
已知一边及一锐角.
sinA= ,sinB= ,
a
c
b
c
= = .
a
sinA
b
sinB
c
sinC
A
B
C
a
b
c
怎样解斜三角形?
5.9 正弦定理、余弦定理
1.正弦定理
在一个三角形中各边和它所对角的正弦的比相等.
= =
a
sinA
b
sinB
c
sinC
=
正弦定理
?
= =
a
sinA
b
sinB
c
sinC
=2R.
=2R
b
sinB
B`
A
B
C
b
O
A
B
C
b
O
B`
A
B
C
b
O
例 1:在 ABC中,已知c=10,A=45°,
C=30°,求b.
解:
∵ = ,
b
sinB
c
sinC
B=180°– (A+C)=105°,
A
B
C
c
b
b = ≈19.
c sinB
sinC
∴
例 2:在 ABC中,已知a=20,b=28,
A=40°,求B和c.
解:
∵ sinB= ≈0.8999
b sinA
a
∴ B1=64°,B2=116°
40°
A
B
C
b
B1
B2
······
在例 2 中,将已知条件改为以下几种情况,结果如何?
(1) b=20,A=60°,a=20√3 ;
(2) b=20,A=60°,a=10√3 ;
(3) b=20,A=60°,a=15.
60°
A
B
C
b
(1) b=20,A=60°,a=20√3
sinB= = ,
b sinA
a
1
2
B=30°或150°,
∵ 150°+60°> 180°,
∴ B=150°应舍去.
60°
20
20√3
A
B
C
(2) b=20,A=60°,a=10√3
sinB= =1 ,
b sinA
a
B=90°.
B
60°
A
C
20
(3) b=20,A=60°,a=15.
sinB= = ,
b sinA
a
2√3
3
2√3
3
∵ > 1,
∴ 无解.
60°
20
A
C
思考: 当b=20,A=60°,a=?时,
有1解、2解、无解.
例 3:已知向量a与a+b夹角为60°,
且 a =8,b =7,求a与b的夹角及a·b.
解:
在 OAC中,
b
sin60°
a
sin∠OCA
∵ =
∴ sin∠OCA= ≈0.9897,
8 sin60°
7
∴ ∠OCA=81.8°或98.2°,
∴ ∠OAC=38.2°或21.8°,
过O作OB∥AC,
∠AOB=141.8°或158.2°,
∴ a·b= a b cos∠AOB=-44.0或-52.
60°
a
a+b
O
A
C1
C2
B1
B2
√2
30°
练习
ABC中,
(1)已知c=√3,A=45°,B=75°,
则a=____,
(2)已知c=2,A=120°,a=2√3,
则B=____,
(3)已知c=2,A=45°,a= ,则
B=_____________.
2√6
3
75°或15°
小结
2. 正弦定理可解以下两种类型的三角形:
(1)已知两角及一边;
(2)已知两边及其中一边的对角.
1. 正弦定理
是解斜三角形的工具之一.
= =
a
sinA
b
sinB
c
sinC
=2R
今日作业
(1)P131 练习
1、2;
(2)习题5.9
第1、2、3题.
选作题
如图,墙上有一个三角形灯架OAB,灯所受重力为10N,OA、OB都是细杆,只能受延杆方向的力,试求杆OA、OB所受的力.
A
B
O
70°
50°
例 3:已知向量a与a+b夹角为60°,
且 a =8,b =7,求a与b的夹角及a·b.
思考:是否可以先求a·(a+b),再求a·b 及a与b
的夹角
高一 数学
课题: 正弦定理
授课人:肖俊妮
怎样解直角三角形?
已知两边;
已知一边及一锐角.
sinA= ,sinB= ,
a
c
b
c
= = .
a
sinA
b
sinB
c
sinC
A
B
C
a
b
c
怎样解斜三角形?
5.9 正弦定理、余弦定理
1.正弦定理
在一个三角形中各边和它所对角的正弦的比相等.
= =
a
sinA
b
sinB
c
sinC
=
正弦定理
?
= =
a
sinA
b
sinB
c
sinC
=2R.
=2R
b
sinB
B`
A
B
C
b
O
A
B
C
b
O
B`
A
B
C
b
O
例 1:在 ABC中,已知c=10,A=45°,
C=30°,求b.
解:
∵ = ,
b
sinB
c
sinC
B=180°– (A+C)=105°,
A
B
C
c
b
b = ≈19.
c sinB
sinC
∴
例 2:在 ABC中,已知a=20,b=28,
A=40°,求B和c.
解:
∵ sinB= ≈0.8999
b sinA
a
∴ B1=64°,B2=116°
40°
A
B
C
b
B1
B2
······
在例 2 中,将已知条件改为以下几种情况,结果如何?
(1) b=20,A=60°,a=20√3 ;
(2) b=20,A=60°,a=10√3 ;
(3) b=20,A=60°,a=15.
60°
A
B
C
b
(1) b=20,A=60°,a=20√3
sinB= = ,
b sinA
a
1
2
B=30°或150°,
∵ 150°+60°> 180°,
∴ B=150°应舍去.
60°
20
20√3
A
B
C
(2) b=20,A=60°,a=10√3
sinB= =1 ,
b sinA
a
B=90°.
B
60°
A
C
20
(3) b=20,A=60°,a=15.
sinB= = ,
b sinA
a
2√3
3
2√3
3
∵ > 1,
∴ 无解.
60°
20
A
C
思考: 当b=20,A=60°,a=?时,
有1解、2解、无解.
例 3:已知向量a与a+b夹角为60°,
且 a =8,b =7,求a与b的夹角及a·b.
解:
在 OAC中,
b
sin60°
a
sin∠OCA
∵ =
∴ sin∠OCA= ≈0.9897,
8 sin60°
7
∴ ∠OCA=81.8°或98.2°,
∴ ∠OAC=38.2°或21.8°,
过O作OB∥AC,
∠AOB=141.8°或158.2°,
∴ a·b= a b cos∠AOB=-44.0或-52.
60°
a
a+b
O
A
C1
C2
B1
B2
√2
30°
练习
ABC中,
(1)已知c=√3,A=45°,B=75°,
则a=____,
(2)已知c=2,A=120°,a=2√3,
则B=____,
(3)已知c=2,A=45°,a= ,则
B=_____________.
2√6
3
75°或15°
小结
2. 正弦定理可解以下两种类型的三角形:
(1)已知两角及一边;
(2)已知两边及其中一边的对角.
1. 正弦定理
是解斜三角形的工具之一.
= =
a
sinA
b
sinB
c
sinC
=2R
今日作业
(1)P131 练习
1、2;
(2)习题5.9
第1、2、3题.
选作题
如图,墙上有一个三角形灯架OAB,灯所受重力为10N,OA、OB都是细杆,只能受延杆方向的力,试求杆OA、OB所受的力.
A
B
O
70°
50°
例 3:已知向量a与a+b夹角为60°,
且 a =8,b =7,求a与b的夹角及a·b.
思考:是否可以先求a·(a+b),再求a·b 及a与b
的夹角
