高一正弦定理(第一课时)课件[下学期]
文档属性
| 名称 | 高一正弦定理(第一课时)课件[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 144.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-05-18 00:00:00 | ||
图片预览

文档简介
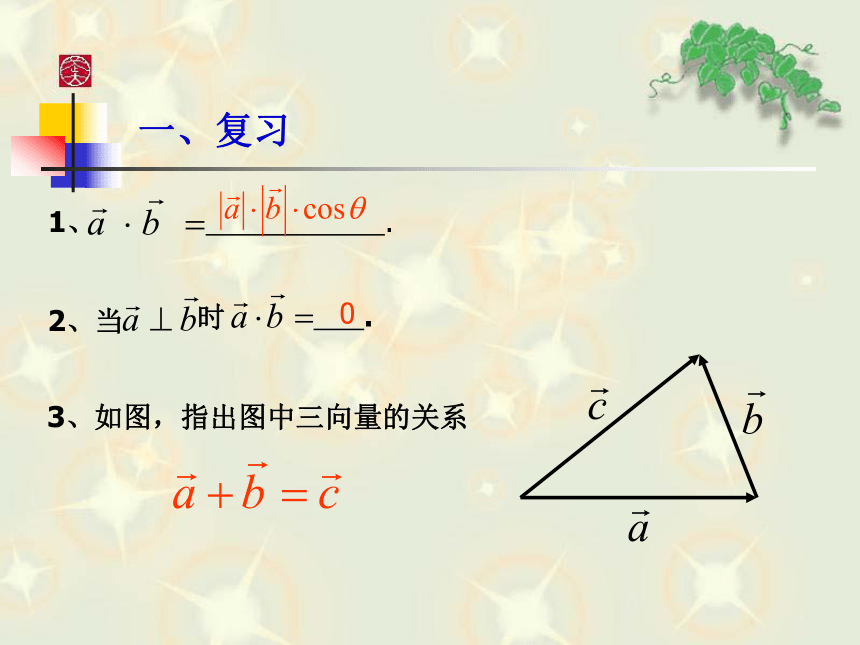
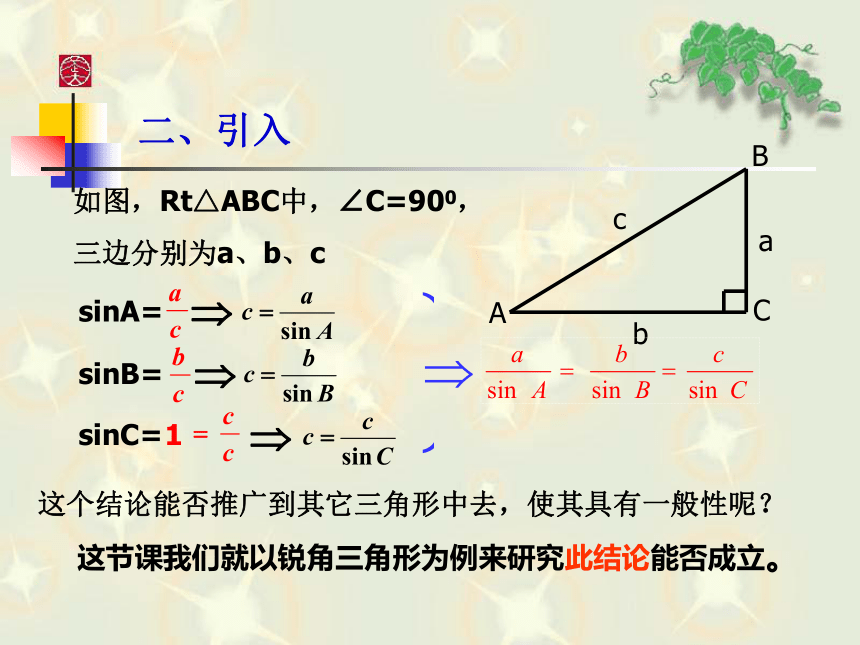
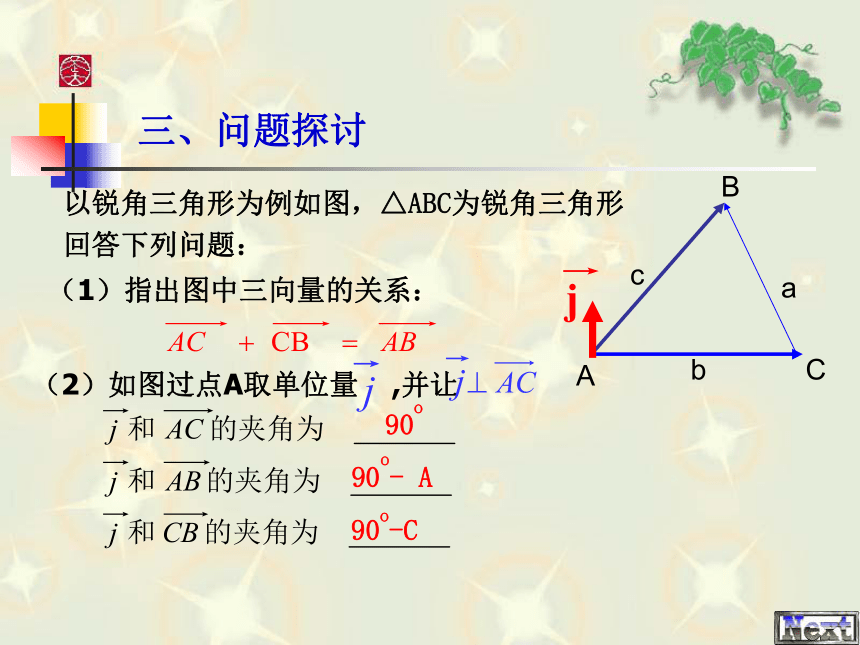
课件16张PPT。一、复习0二、引入sinA=sinB=sinC=1三、问题探讨以锐角三角形为例如图,△ABC为锐角三角形
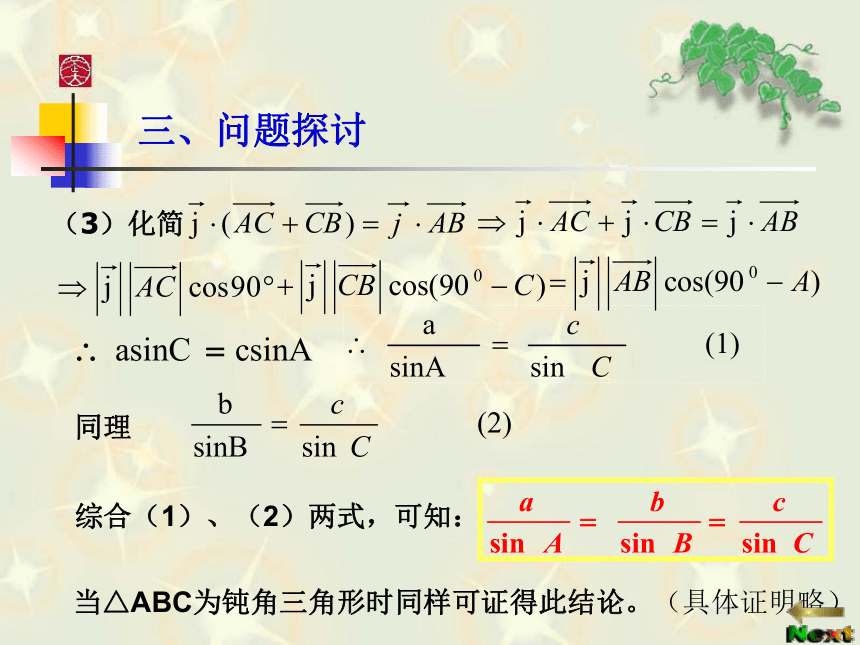
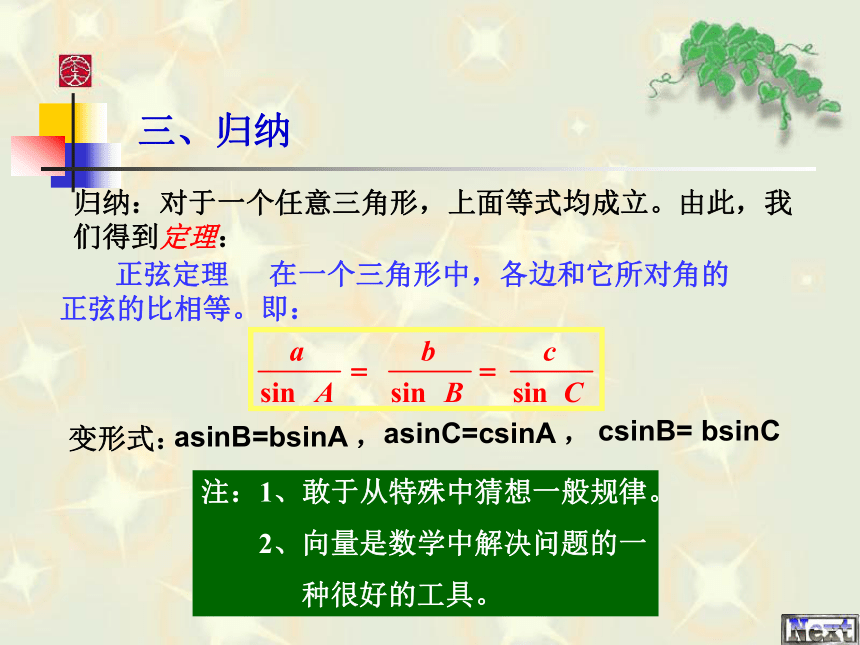
回答下列问题:(1)指出图中三向量的关系:90o-C90o90o- A三、问题探讨综合(1)、(2)两式,可知:当△ABC为钝角三角形时同样可证得此结论。(具体证明略)三、归纳归纳:对于一个任意三角形,上面等式均成立。由此,我们得到定理: 正弦定理 在一个三角形中,各边和它所对角的正弦的比相等。即:asinC=csinA , asinB=bsinA ,csinB= bsinC变形式:注:1、敢于从特殊中猜想一般规律。
2、向量是数学中解决问题的一
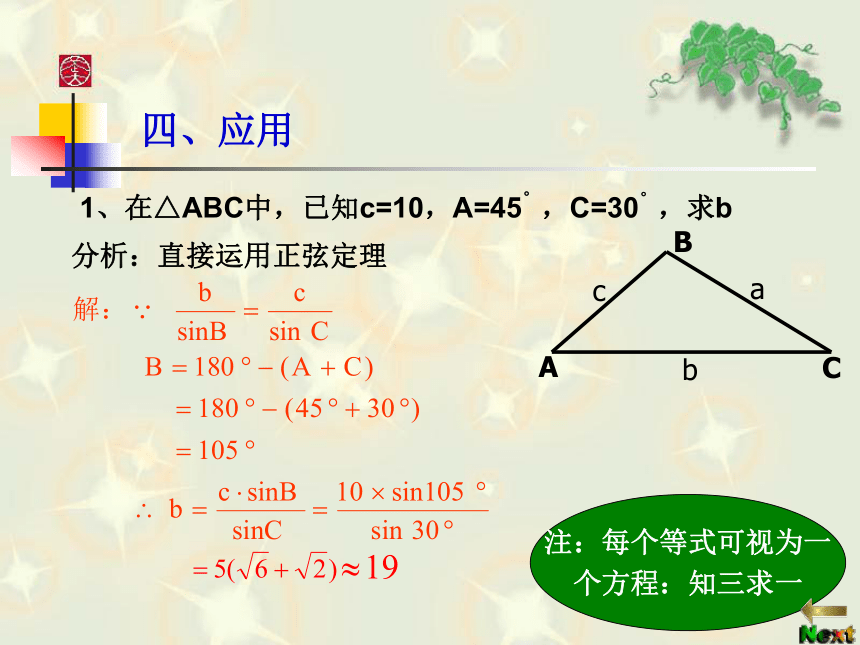
种很好的工具。四、应用 1、在△ABC中,已知c=10,A=45。,C=30。,求b 分析:直接运用正弦定理注:每个等式可视为一
个方程:知三求一 2:在?ABC中,已知a= ,b= ,A=45°,求B和c. 四、应用∴ B1=60°,B2=120°······四、应用一解一解无解ab无解一解两解一解无解一解条件图形四、总结五、练习六、小结2. 正弦定理可解以下两种类型的三角形:
(1)已知两角及一边;
(2)已知两边及其中一边的对角.如果已知两边及其夹角,如何解三角形呢?拓展思维与能力培养:1、课堂上,我们一起用向量证明了直角和锐角三角形
满足正弦定理 ,思考如何用向量证明钝角三角形
满足正弦定理 ?
2、正弦定理 还有其他方法证明吗?(其中2R是△ABC的外接圆直径。)3、正弦定理 还可表示为拓展思维与能力培养:1、课堂上,我们一起用向量证明了直角和锐角三角形
满足正弦定理 ,思考如何用向量证明钝角三角形
满足正弦定理 ?
2、正弦定理 还有其他方法证明吗?3、正弦定理 还可表示为(其中2R是△ABC的外接圆直径。)2R七、作业:1、课本P134 第2题
2、△ABC中,已知a=20,
∠B=600,∠C=450,求边c和b。谢 谢 大 家
回答下列问题:(1)指出图中三向量的关系:90o-C90o90o- A三、问题探讨综合(1)、(2)两式,可知:当△ABC为钝角三角形时同样可证得此结论。(具体证明略)三、归纳归纳:对于一个任意三角形,上面等式均成立。由此,我们得到定理: 正弦定理 在一个三角形中,各边和它所对角的正弦的比相等。即:asinC=csinA , asinB=bsinA ,csinB= bsinC变形式:注:1、敢于从特殊中猜想一般规律。
2、向量是数学中解决问题的一
种很好的工具。四、应用 1、在△ABC中,已知c=10,A=45。,C=30。,求b 分析:直接运用正弦定理注:每个等式可视为一
个方程:知三求一 2:在?ABC中,已知a= ,b= ,A=45°,求B和c. 四、应用∴ B1=60°,B2=120°······四、应用一解一解无解a
(1)已知两角及一边;
(2)已知两边及其中一边的对角.如果已知两边及其夹角,如何解三角形呢?拓展思维与能力培养:1、课堂上,我们一起用向量证明了直角和锐角三角形
满足正弦定理 ,思考如何用向量证明钝角三角形
满足正弦定理 ?
2、正弦定理 还有其他方法证明吗?(其中2R是△ABC的外接圆直径。)3、正弦定理 还可表示为拓展思维与能力培养:1、课堂上,我们一起用向量证明了直角和锐角三角形
满足正弦定理 ,思考如何用向量证明钝角三角形
满足正弦定理 ?
2、正弦定理 还有其他方法证明吗?3、正弦定理 还可表示为(其中2R是△ABC的外接圆直径。)2R七、作业:1、课本P134 第2题
2、△ABC中,已知a=20,
∠B=600,∠C=450,求边c和b。谢 谢 大 家
