华东师大版八年级数学上册 第14章 勾股定理 折叠问题中的勾股定理 课件 (共18张PPT)
文档属性
| 名称 | 华东师大版八年级数学上册 第14章 勾股定理 折叠问题中的勾股定理 课件 (共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 520.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-08 09:07:50 | ||
图片预览




文档简介
(共18张PPT)
折叠问题中的勾股定理
勾股定理反映的是直角三角形三边
的关系。应用勾股定理由已知边求出
未知边。
这节课应用勾股定理来解决折叠中
的诸多问题
引入:
请按下列要求折叠矩形纸片ABCD
并画出折叠后的几何图形
1:把矩形边AB折在边AD上。
2:把矩形ABCD边AB 折在对角线AC上。
3:把矩形ABCD沿对角线AC对折。
4: 使矩形的顶点B恰好与点D重合。
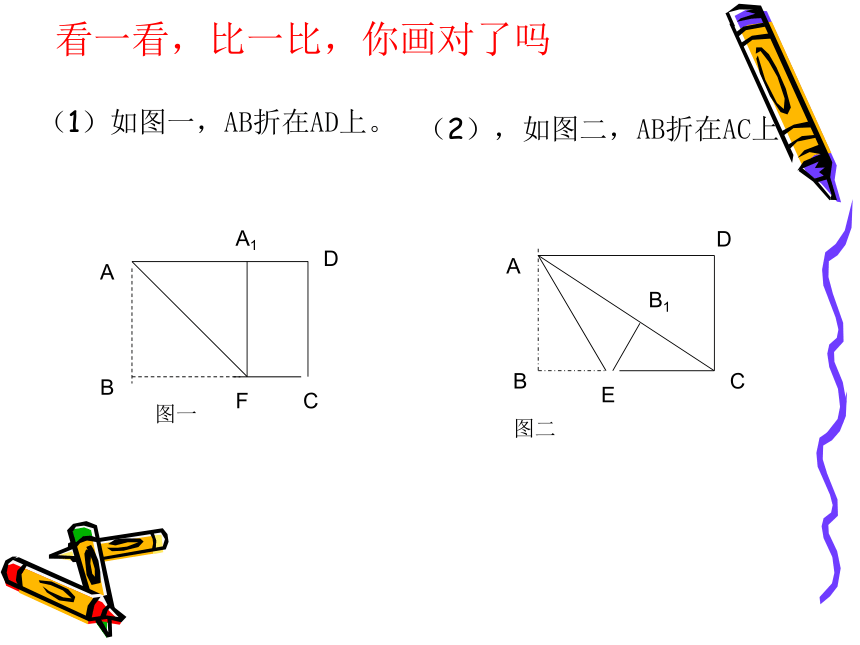
看一看,比一比,你画对了吗
图一
A
B
C
D
A1
F
A
B
C
D
E
B1
图二
(1)如图一,AB折在AD上。
(2),如图二,AB折在AC上
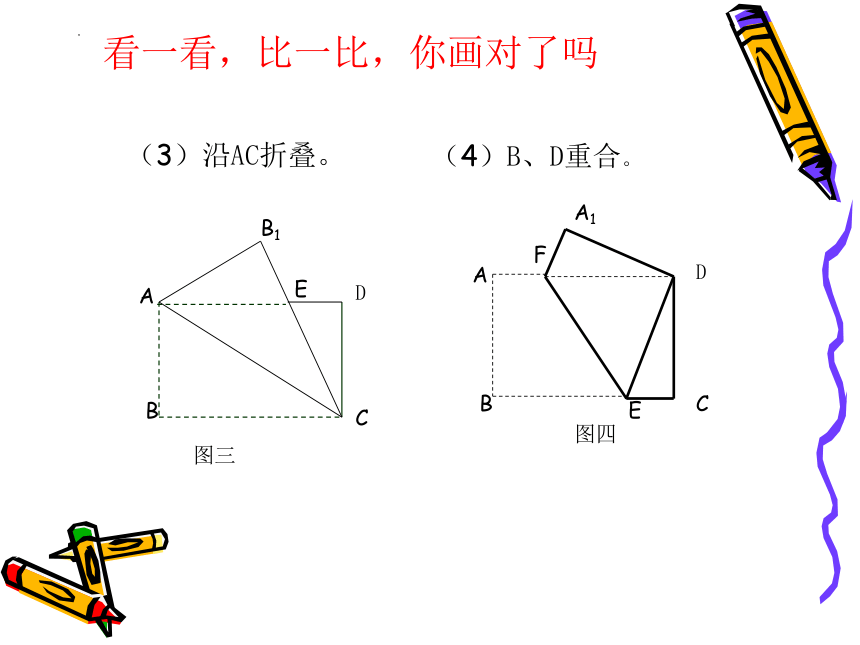
看一看,比一比,你画对了吗
A
B
C
D
E
B1
图三
A
B
C
D
E
F
A1
图四
(3)沿AC折叠。
(4)B、D重合。
问题1:如图一,若AB=6,AD=8,你能求出图中哪些线段的长度?
A
D
C
E
B
B1
AB=AB1=CD=BE=6,
B1D=EC=2,
AE2=AB2+BE2
=62+62=72
AE=
探究新知
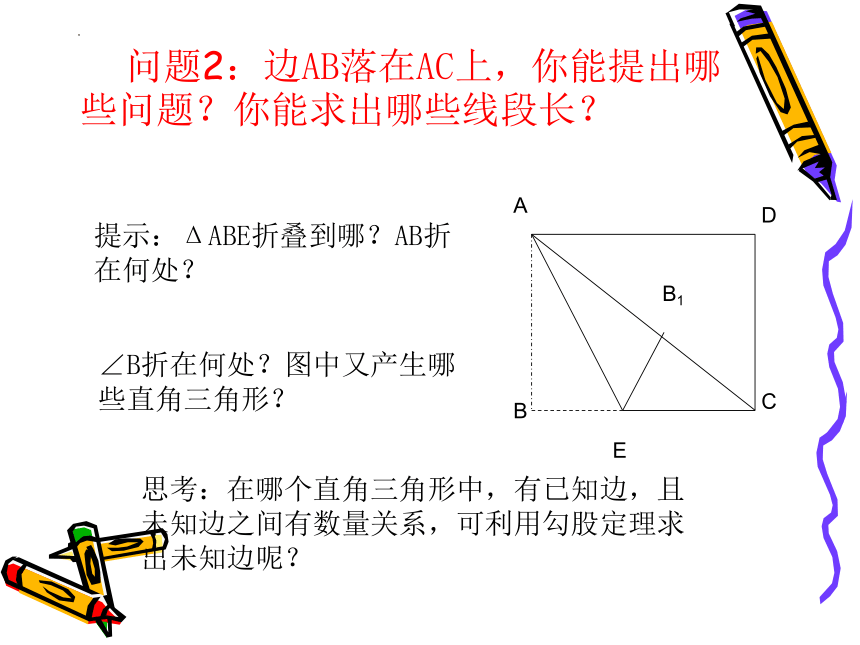
问题2:边AB落在AC上,你能提出哪些问题?你能求出哪些线段长?
A
D
C
B
E
B1
提示:ΔABE折叠到哪?AB折在何处?
∠B折在何处?图中又产生哪些直角三角形?
思考:在哪个直角三角形中,有已知边,且未知边之间有数量关系,可利用勾股定理求出未知边呢?
问题2:
A
D
C
B
E
B1
1:AB=AB1=CD=6,AD=BC=8,∠B=∠AB1E=∠EB1C=
900.求: AC= B1C=
3:△EB1C中B1C=4, B1E+CE=10
设B1E=x,则EC=6-x。根据勾股
定理,可得方程
x2+42=(8-x)2 解得 x=3
则BE=B1E=3,CE=5 下一步可求得AE.
2:思考:怎么求出BE,CE呢
问题3:把矩形ABCD沿对角线AC折叠,如下图
所示。你能提出哪些问题?
2.思考: △ABC折在何处?图中哪些直
角三角形有已知边,且知道未知两边之和。
3. △EDC的面积是多少?
A
B
C
D
E
B1
1
2
3
1. △AEC是什么三角形?
⑴∵ AD∥BC
∴ ∠ 1=∠2
∵ ∠2=∠3
∴ ∠ 1=∠3
∴AE=EC
⑵设ED=x,则EC=AE=8-x.
根据勾股定理,得
ED2+DC2=EC2
即x2+62=(8-x)2
解得x=
∴S△EDC= ED·DC= × ×6
=
A
B
C
D
E
B1
1
2
3
△AB1E同ΔEDC.
问题4.折叠矩形ABCD,使点B与点D重合。如下图。你能提出哪些问题?
A
B
C
D
E
F
A1
参照问题3,可以得出DE等于哪一
条线段 (DE=DF)
知道了DE的值,你能求出折痕
EF的值吗
A
B
D
E
B1
1
2
3
C
同前面,找找哪个直角三角形可由勾股定理由
已知边求出未知边?(ΔA1FB与ΔBEC)
过点F作FG⊥BC于G。同问题3,得
CE= ,BE=DE=DF= 。
解:在ΔDEC中,设CE=x,则
DE=BE=8-x,
由勾股定理
得:x2+62=(8-x)2
x=
A
B
C
D
E
F
A1
G
ΔA1FD同ΔCED.可得A1F=AF=
在Rt△EFG中,
GE= - =
A
B
C
D
E
F
A1
G
概括:找出图中的直角三角形,用勾股定理求出
未知边。
怎么求EF?做垂线,构造直角三角形。
EF2=FG2+GE2
=62 +( )2 =
∴EF=
总结:怎么应用勾股定理解决折叠问题?
1.抓住折叠前后的图形是全等形,找出图
中的直角三角形(可做垂线段构造直角三角
形)。
2.设未知数,找等量关系,根据直角三角形
的三边关系列方程(组)。
课堂练习:
如图,有一张直角三角形纸片,两直角边AC=6cm,BC=8cm,
现将ΔABC沿直线AD折叠,使AC落在斜边AB上,且与AE重合,
求BD的长。
解:AC=6,BC=8,∠C=900.
则AB=10
∵AE=AC=6
∴BE=10-6=4
B
A
C
E
D
在RtΔDEB中:设CD=DE=x,设DB=8-x.
由勾股定理得:
x2+42=(8-x)2
得x=3.
∴DB=5
课后作业:
1,如图,在长方形纸片ABCD中,AB=12,BC=5,点E在AB上将ΔADE沿DE折叠,使点A落在对角线BD上的点A1处,则AE的长为多少?
D
A
E
A1
C
B
2,如图是长方形纸片ABCD折叠的情况,纸片的宽AB=8厘米,长AD=10厘米,AD沿点A对折,点D正好落在BC的点D1,AE是折痕。
(1)求BD1的长。
(2)若设CE为x,请用含x的代数式表示线段D1E的长。
(3)求四边形ABCE的面积。
A
B
D1
D
E
C
折叠问题中的勾股定理
勾股定理反映的是直角三角形三边
的关系。应用勾股定理由已知边求出
未知边。
这节课应用勾股定理来解决折叠中
的诸多问题
引入:
请按下列要求折叠矩形纸片ABCD
并画出折叠后的几何图形
1:把矩形边AB折在边AD上。
2:把矩形ABCD边AB 折在对角线AC上。
3:把矩形ABCD沿对角线AC对折。
4: 使矩形的顶点B恰好与点D重合。
看一看,比一比,你画对了吗
图一
A
B
C
D
A1
F
A
B
C
D
E
B1
图二
(1)如图一,AB折在AD上。
(2),如图二,AB折在AC上
看一看,比一比,你画对了吗
A
B
C
D
E
B1
图三
A
B
C
D
E
F
A1
图四
(3)沿AC折叠。
(4)B、D重合。
问题1:如图一,若AB=6,AD=8,你能求出图中哪些线段的长度?
A
D
C
E
B
B1
AB=AB1=CD=BE=6,
B1D=EC=2,
AE2=AB2+BE2
=62+62=72
AE=
探究新知
问题2:边AB落在AC上,你能提出哪些问题?你能求出哪些线段长?
A
D
C
B
E
B1
提示:ΔABE折叠到哪?AB折在何处?
∠B折在何处?图中又产生哪些直角三角形?
思考:在哪个直角三角形中,有已知边,且未知边之间有数量关系,可利用勾股定理求出未知边呢?
问题2:
A
D
C
B
E
B1
1:AB=AB1=CD=6,AD=BC=8,∠B=∠AB1E=∠EB1C=
900.求: AC= B1C=
3:△EB1C中B1C=4, B1E+CE=10
设B1E=x,则EC=6-x。根据勾股
定理,可得方程
x2+42=(8-x)2 解得 x=3
则BE=B1E=3,CE=5 下一步可求得AE.
2:思考:怎么求出BE,CE呢
问题3:把矩形ABCD沿对角线AC折叠,如下图
所示。你能提出哪些问题?
2.思考: △ABC折在何处?图中哪些直
角三角形有已知边,且知道未知两边之和。
3. △EDC的面积是多少?
A
B
C
D
E
B1
1
2
3
1. △AEC是什么三角形?
⑴∵ AD∥BC
∴ ∠ 1=∠2
∵ ∠2=∠3
∴ ∠ 1=∠3
∴AE=EC
⑵设ED=x,则EC=AE=8-x.
根据勾股定理,得
ED2+DC2=EC2
即x2+62=(8-x)2
解得x=
∴S△EDC= ED·DC= × ×6
=
A
B
C
D
E
B1
1
2
3
△AB1E同ΔEDC.
问题4.折叠矩形ABCD,使点B与点D重合。如下图。你能提出哪些问题?
A
B
C
D
E
F
A1
参照问题3,可以得出DE等于哪一
条线段 (DE=DF)
知道了DE的值,你能求出折痕
EF的值吗
A
B
D
E
B1
1
2
3
C
同前面,找找哪个直角三角形可由勾股定理由
已知边求出未知边?(ΔA1FB与ΔBEC)
过点F作FG⊥BC于G。同问题3,得
CE= ,BE=DE=DF= 。
解:在ΔDEC中,设CE=x,则
DE=BE=8-x,
由勾股定理
得:x2+62=(8-x)2
x=
A
B
C
D
E
F
A1
G
ΔA1FD同ΔCED.可得A1F=AF=
在Rt△EFG中,
GE= - =
A
B
C
D
E
F
A1
G
概括:找出图中的直角三角形,用勾股定理求出
未知边。
怎么求EF?做垂线,构造直角三角形。
EF2=FG2+GE2
=62 +( )2 =
∴EF=
总结:怎么应用勾股定理解决折叠问题?
1.抓住折叠前后的图形是全等形,找出图
中的直角三角形(可做垂线段构造直角三角
形)。
2.设未知数,找等量关系,根据直角三角形
的三边关系列方程(组)。
课堂练习:
如图,有一张直角三角形纸片,两直角边AC=6cm,BC=8cm,
现将ΔABC沿直线AD折叠,使AC落在斜边AB上,且与AE重合,
求BD的长。
解:AC=6,BC=8,∠C=900.
则AB=10
∵AE=AC=6
∴BE=10-6=4
B
A
C
E
D
在RtΔDEB中:设CD=DE=x,设DB=8-x.
由勾股定理得:
x2+42=(8-x)2
得x=3.
∴DB=5
课后作业:
1,如图,在长方形纸片ABCD中,AB=12,BC=5,点E在AB上将ΔADE沿DE折叠,使点A落在对角线BD上的点A1处,则AE的长为多少?
D
A
E
A1
C
B
2,如图是长方形纸片ABCD折叠的情况,纸片的宽AB=8厘米,长AD=10厘米,AD沿点A对折,点D正好落在BC的点D1,AE是折痕。
(1)求BD1的长。
(2)若设CE为x,请用含x的代数式表示线段D1E的长。
(3)求四边形ABCE的面积。
A
B
D1
D
E
C
