正弦定理(第一课时)[下学期]
图片预览
文档简介
课 题:正弦定理
第一课时
望城六中 欧阳立松
教学目标:
1.知识目标:理解正弦定理的向量证明方法,掌握正弦定理。
2.能力目标:培养观察,归纳,猜想,探究的思维方法与能力。
3.情感目标:培养合作交流、独立思考等良好的个性品质;以及勇于创新的科学精神。
重点与难点
重点:正弦定理的探究和简单应用。
难点:利用向量的方法证明正弦定理。
教 具:多媒体课件、投影仪、三角板
教学方法:探究启发、自学辅导法
授课类型:新授课
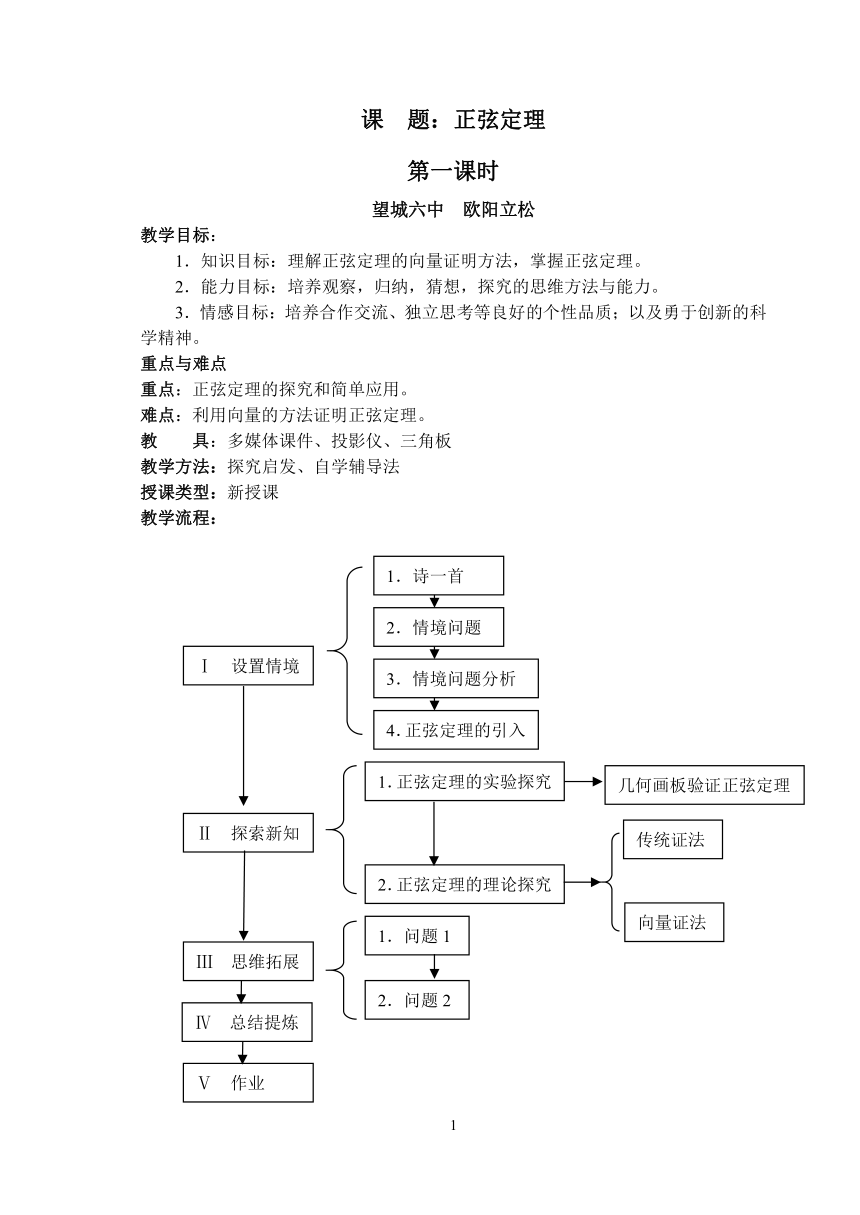
教学流程:
教学过程:
Ⅰ情境设置
1.利用课前几分钟,借助于多媒体展示有关的数学史:《九章算术注》和刘徽、勾股定理的介绍。
2.借助于多媒体展示诗一首:
近测高塔远看山,量天度海只等闲。
古有九章勾股法,今看三角正余弦。
3.情境设问
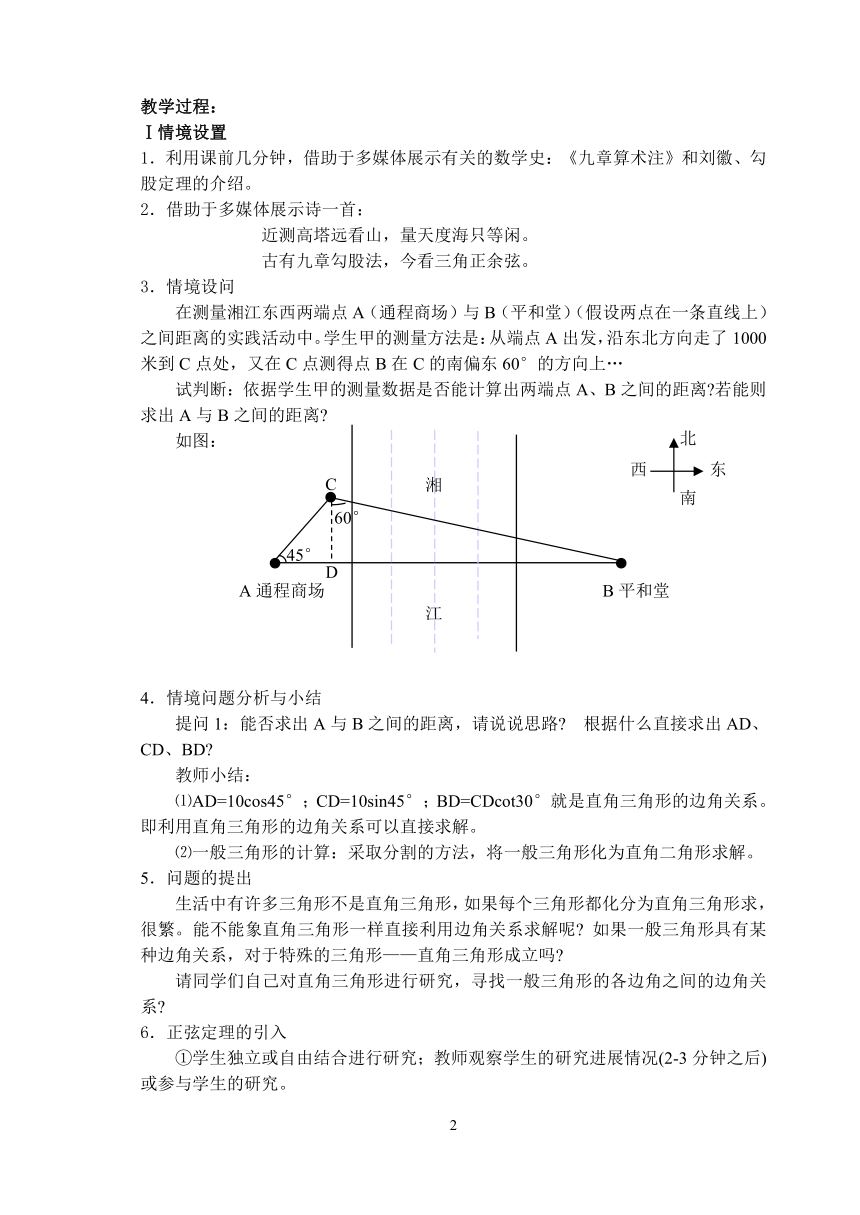
在测量湘江东西两端点A(通程商场)与B(平和堂)(假设两点在一条直线上)之间距离的实践活动中。学生甲的测量方法是:从端点A出发,沿东北方向走了1000米到C点处,又在C点测得点B在C的南偏东60°的方向上…
试判断:依据学生甲的测量数据是否能计算出两端点A、B之间的距离 若能则求出A与B之间的距离
如图:
4.情境问题分析与小结
提问1:能否求出A与B之间的距离,请说说思路 根据什么直接求出AD、CD、BD
教师小结:
⑴AD=10cos45°;CD=10sin45°;BD=CDcot30°就是直角三角形的边角关系。即利用直角三角形的边角关系可以直接求解。
⑵一般三角形的计算:采取分割的方法,将一般三角形化为直角二角形求解。
5.问题的提出
生活中有许多三角形不是直角三角形,如果每个三角形都化分为直角三角形求,很繁。能不能象直角三角形一样直接利用边角关系求解呢 如果一般三角形具有某种边角关系,对于特殊的三角形——直角三角形成立吗
请同学们自己对直角三角形进行研究,寻找一般三角形的各边角之间的边角关系
6.正弦定理的引入
①学生独立或自由结合进行研究;教师观察学生的研究进展情况(2-3分钟之后)或参与学生的研究。
②展示学生研究的结果
③猜测结论:a:sinA=b:sinB=c:sinC对于一般三角形是否成立
Ⅱ 探索新知
1.正弦定理的实验探究:
实验探究正弦定理(利用《几何画板》软件已经制作的教学课件演示正弦定理)a:sinA=b:sinB=c:sinC是否对任意三角形都成立呢 现在借助于《几何画板》作实验验证。
(1)引导观察三角形形状的变化
(2)显示三个比值:观察随角的变化即为锐角、钝角时比值的变化情况。
结论:a:sinA=b:sinB=c:sinC对于任意三角形都成立。
2.正弦定理的理论探究
探究方案:
直角三角形——已证明
锐角三角形——课堂探究(且仅证明c:sinC=b: sinB)
钝角三角形——课后证明
(1)学生独立或自由组合在锐角三角形中进行定理证明思路的探究且仅证明c:sinC=b: sinB,教师参与学生的研究过程,并及时指导学生的研究。
⑵提问2:能否运用向量的方法证明呢 什么知识可把长度和三角函数联系起来?
⑶提问3:对比结构差异,如何找到作数量积的两个因式的向量?请同学们翻开课本,看正弦定理的证明方法,并问答问题(学生阅读课本3-5分钟)
提问4:为什么要做单位向量,引入单位向量有什么作用
提问5:不过点A作,可以吗 单位向量的方向与所作的单位向量的方向相反,可以吗 所作的向量不是单位向量可以吗
3.正弦定理:在一个三角形中,各边和它所对角的正弦比相等,
即
定理剖析:
⑴从表达式的结构来看,表达了对边与对角的正弦比,有严谨的、和谐的对应关系;
⑵从方程的观点看,正弦定理有三个等式,可视为三个方程,每个方程含有四个量,知其三可求其一;
⑶从应用的途径看,正弦定理适用于任意三角形,可解决两类有关的三角形问题。
4.试一试 利用正弦定理解决情境问题。
Ⅲ 思维拓展
问题1:如右图,圆O为△ABC的外接圆,R为其半径,== =2R成立吗 并证明之?
问题2:正弦定理还有其它证明方法吗(例如利用三角形的面积、外接圆、向量的坐标等)?试探索之。
Ⅳ 总结提炼
本节课,同学们探究了正弦定理及其证明方法,并应用正弦定理解决了一个生活实际问题,正弦定理还有更广泛的应用,我们下节课再继续探讨。
Ⅴ 作业 完成思维拓展题,并预习教材正弦定理的应用P130-P131。
2.问题2
1.问题1
2.正弦定理的理论探究
1.正弦定理的实验探究
4.正弦定理的引入
3.情境问题分析
2.情境问题
1.诗一首
Ⅳ 总结提炼
Ⅲ 思维拓展
Ⅱ 探索新知
Ⅰ 设置情境
几何画板验证正弦定理
传统证法
向量证法
Ⅴ 作业
==
对称美
和谐美
东
D
湘
江
60°
B平和堂
A通程商场
45°
C
西
南
北
PAGE
1
第一课时
望城六中 欧阳立松
教学目标:
1.知识目标:理解正弦定理的向量证明方法,掌握正弦定理。
2.能力目标:培养观察,归纳,猜想,探究的思维方法与能力。
3.情感目标:培养合作交流、独立思考等良好的个性品质;以及勇于创新的科学精神。
重点与难点
重点:正弦定理的探究和简单应用。
难点:利用向量的方法证明正弦定理。
教 具:多媒体课件、投影仪、三角板
教学方法:探究启发、自学辅导法
授课类型:新授课
教学流程:
教学过程:
Ⅰ情境设置
1.利用课前几分钟,借助于多媒体展示有关的数学史:《九章算术注》和刘徽、勾股定理的介绍。
2.借助于多媒体展示诗一首:
近测高塔远看山,量天度海只等闲。
古有九章勾股法,今看三角正余弦。
3.情境设问
在测量湘江东西两端点A(通程商场)与B(平和堂)(假设两点在一条直线上)之间距离的实践活动中。学生甲的测量方法是:从端点A出发,沿东北方向走了1000米到C点处,又在C点测得点B在C的南偏东60°的方向上…
试判断:依据学生甲的测量数据是否能计算出两端点A、B之间的距离 若能则求出A与B之间的距离
如图:
4.情境问题分析与小结
提问1:能否求出A与B之间的距离,请说说思路 根据什么直接求出AD、CD、BD
教师小结:
⑴AD=10cos45°;CD=10sin45°;BD=CDcot30°就是直角三角形的边角关系。即利用直角三角形的边角关系可以直接求解。
⑵一般三角形的计算:采取分割的方法,将一般三角形化为直角二角形求解。
5.问题的提出
生活中有许多三角形不是直角三角形,如果每个三角形都化分为直角三角形求,很繁。能不能象直角三角形一样直接利用边角关系求解呢 如果一般三角形具有某种边角关系,对于特殊的三角形——直角三角形成立吗
请同学们自己对直角三角形进行研究,寻找一般三角形的各边角之间的边角关系
6.正弦定理的引入
①学生独立或自由结合进行研究;教师观察学生的研究进展情况(2-3分钟之后)或参与学生的研究。
②展示学生研究的结果
③猜测结论:a:sinA=b:sinB=c:sinC对于一般三角形是否成立
Ⅱ 探索新知
1.正弦定理的实验探究:
实验探究正弦定理(利用《几何画板》软件已经制作的教学课件演示正弦定理)a:sinA=b:sinB=c:sinC是否对任意三角形都成立呢 现在借助于《几何画板》作实验验证。
(1)引导观察三角形形状的变化
(2)显示三个比值:观察随角的变化即为锐角、钝角时比值的变化情况。
结论:a:sinA=b:sinB=c:sinC对于任意三角形都成立。
2.正弦定理的理论探究
探究方案:
直角三角形——已证明
锐角三角形——课堂探究(且仅证明c:sinC=b: sinB)
钝角三角形——课后证明
(1)学生独立或自由组合在锐角三角形中进行定理证明思路的探究且仅证明c:sinC=b: sinB,教师参与学生的研究过程,并及时指导学生的研究。
⑵提问2:能否运用向量的方法证明呢 什么知识可把长度和三角函数联系起来?
⑶提问3:对比结构差异,如何找到作数量积的两个因式的向量?请同学们翻开课本,看正弦定理的证明方法,并问答问题(学生阅读课本3-5分钟)
提问4:为什么要做单位向量,引入单位向量有什么作用
提问5:不过点A作,可以吗 单位向量的方向与所作的单位向量的方向相反,可以吗 所作的向量不是单位向量可以吗
3.正弦定理:在一个三角形中,各边和它所对角的正弦比相等,
即
定理剖析:
⑴从表达式的结构来看,表达了对边与对角的正弦比,有严谨的、和谐的对应关系;
⑵从方程的观点看,正弦定理有三个等式,可视为三个方程,每个方程含有四个量,知其三可求其一;
⑶从应用的途径看,正弦定理适用于任意三角形,可解决两类有关的三角形问题。
4.试一试 利用正弦定理解决情境问题。
Ⅲ 思维拓展
问题1:如右图,圆O为△ABC的外接圆,R为其半径,== =2R成立吗 并证明之?
问题2:正弦定理还有其它证明方法吗(例如利用三角形的面积、外接圆、向量的坐标等)?试探索之。
Ⅳ 总结提炼
本节课,同学们探究了正弦定理及其证明方法,并应用正弦定理解决了一个生活实际问题,正弦定理还有更广泛的应用,我们下节课再继续探讨。
Ⅴ 作业 完成思维拓展题,并预习教材正弦定理的应用P130-P131。
2.问题2
1.问题1
2.正弦定理的理论探究
1.正弦定理的实验探究
4.正弦定理的引入
3.情境问题分析
2.情境问题
1.诗一首
Ⅳ 总结提炼
Ⅲ 思维拓展
Ⅱ 探索新知
Ⅰ 设置情境
几何画板验证正弦定理
传统证法
向量证法
Ⅴ 作业
==
对称美
和谐美
东
D
湘
江
60°
B平和堂
A通程商场
45°
C
西
南
北
PAGE
1
