余弦定理[下学期]

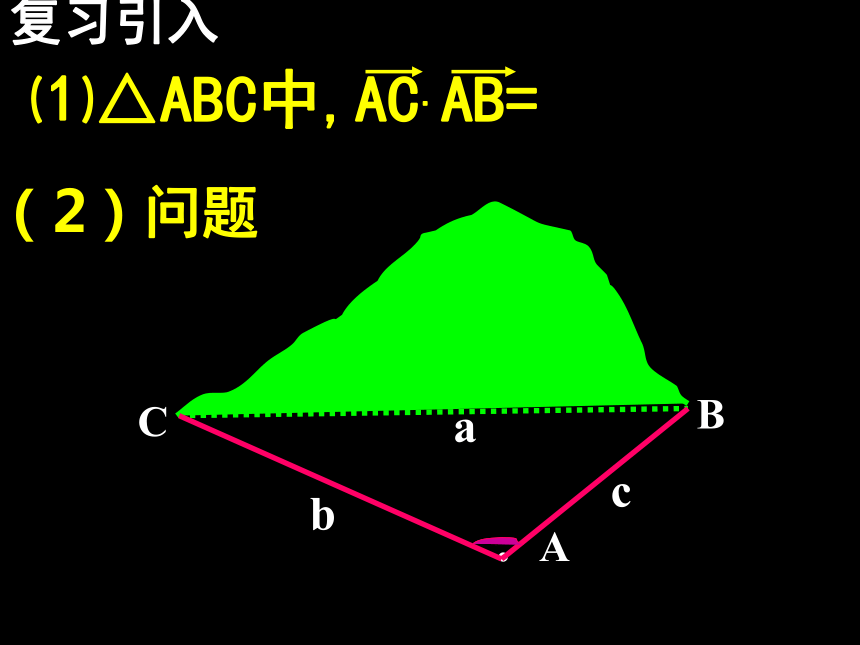
课件8张PPT。余 弦 定 理（一）复习引入⑴△ABC中,AC.AB=. ABCcba（2）问题⑶△ABC中已知AB=c AC=b及A则BC=a=?
ABCcbCC① a=f(A) A∈(0,π)②A=π/2时a2=b2+c2为方便，记a2 =g(A)A=π/2时a2=g(π/2 )=b2+c2③考察极端情况A=π时a2=g(π)=（b+c）2 = b2+c2 +2bc
A=0时a2=g(0)=（b-c）2 = b2+c2 -2bc
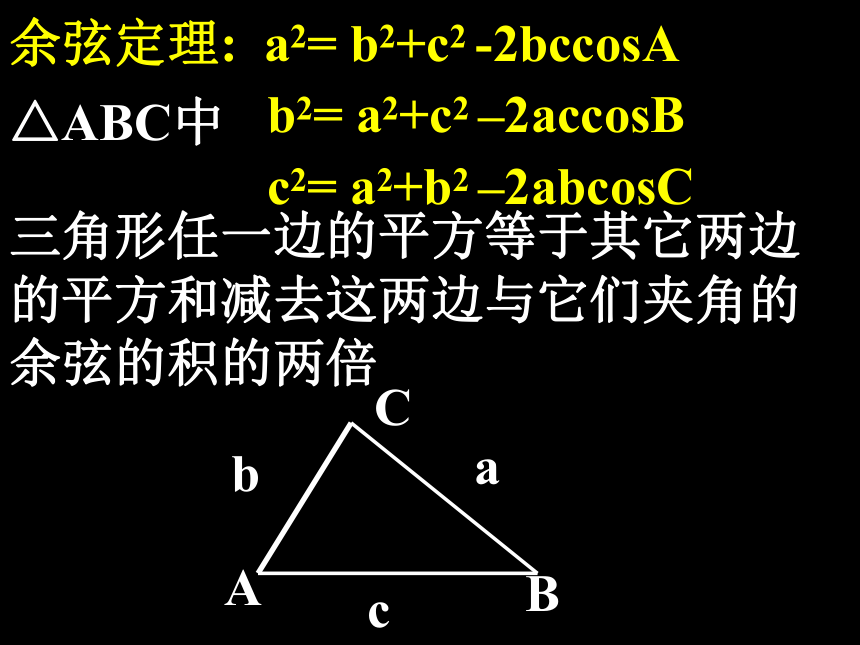
余弦定理: a2= b2+c2 -2bccosA
b2= a2+c2 –2accosBc2= a2+b2 –2abcosCAB
C
b
a
c
三角形任一边的平方等于其它两边的平方和减去这两边与它们夹角的余弦的积的两倍
△ABC中例1 △ABC中b=8 c=3 A=600, 求a
例2 ⑴△ABC中a=9 b=10 c=15,求A⑵△ABC中a=7 b=5 c=3,求A,B
cosA=
b2+c2 -a2
2bc
cosB=
a2+c2 -b2
2accosC=
a2+b2 -c22ab
例3 △ABC中三边长为2，3，4则此三角形为（ ）练习：
⑴△ABC中a2= b2+c2 +bc，则A=( )
⑵△ABC中a2＞ b2+c2 ，则A是( )角
⑶ △ABC中a2＜ b2+c2 且a边最长，则A角的范围是( )
⑷以4,5,6为边长的三角形一定是( )
三角形120o钝60o再见！再见！再见！