人教版九年级数学上册第二十三章 旋转 单元 检测试题(word版 含答案)
文档属性
| 名称 | 人教版九年级数学上册第二十三章 旋转 单元 检测试题(word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 407.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-08 09:09:54 | ||
图片预览



文档简介
第二十三章 《旋转》单元测试卷
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.下列说法正确的是( )
A.平移不改变图形的形状和大小,而旋转则改变图形的形状和大小
B.平移和旋转的共同点是改变图形的位置
C.图形可以向某方向平移一定距离,也可以向某方向旋转一定距离
D.由平移得到的图形也一定可由旋转得到
2.已知点的坐标为,为坐标原点,连结,将线段绕点按逆时针方向旋转得,则点的坐标为( )
A. B. C. D.
3.如图,在中,,在同一平面内,将绕点按逆时针方向旋转到的位置,使得,则
A. B. C. D.
4.若两个图形关于某一点成中心对称,那么下列说法.正确的是( )
①对称点的连线必过对称中心;②这两个图形一定全等;③对应线段一定平行(或在一条直线上)且相等;④将一个图形绕对称中心旋转必定与另一个图形重合.
A.①② B.①③ C.①②③ D.①②③④
5.如果一个图形绕着一个点至少需要旋转才能与它本身重合,则下列说法正确的是( )
A.这个图形一定是中心对称图形 B.这个图形可能是中心对称图形
C.这个图形旋转后能与它本身重合 D.以上都不对
6.同学们曾玩过万花筒,它是由三块等宽等长的玻璃围成的,图是看到的万花筒的一个图案,图中所有的小三角形均是全等的等边三角形,其中的菱形可以看成是把菱形以点为中心( ).
A.顺时针旋转得到 B.顺时针旋转得到
C.逆时针旋转得到 D.逆时针旋转得到
7. 如图,在平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点B′的坐标是( )
图7-ZT-1
A.(-1,2+) B.(-,3) C.(-,2+) D.(-3,)
8. 若点P(-a,a-3)关于原点对称的点是第二象限内的点,则a满足( )
A.a>3 B.0<a≤3
C.a<0 D.a<0或a>3
9. 如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为 ( )
A.4,30° B.2,60° C.1,30° D.3,60°
10. 在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取一定点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,-300°)或P(3,420°)等,则与点P关于点O对称的点Q的极坐标表示不正确的是( )
A.Q(3,240°) B.Q(3,-120°) C.Q(3,600°) D.Q(3,-500°)
二、填空题(每题3分,共24分)
11.点(a,2)与点(b,-2)关于原点中心对称,则a+b的值是 .
12.如图是4×4的正方形网格,再把其中一个白色小正方形涂上阴影,使整个阴影部分成为轴对称图形,这样的白色小正方形有________个.
13.如图,已知抛物线C1,抛物线C2关于原点对称.若抛物线C1的解析式为y=(x+2)2-1,那么抛物线C2的解析式为 .
14.如图,在平面直角坐标系中,将绕点旋转180°得到,则点的坐标为__________.
15. 已知 ABCD的顶点A在第三象限,对角线AC的中点在坐标原点,一边AB与x轴平行且AB=2.若点A的坐标为(a,b),则点D的坐标为________________.
16.如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为 .
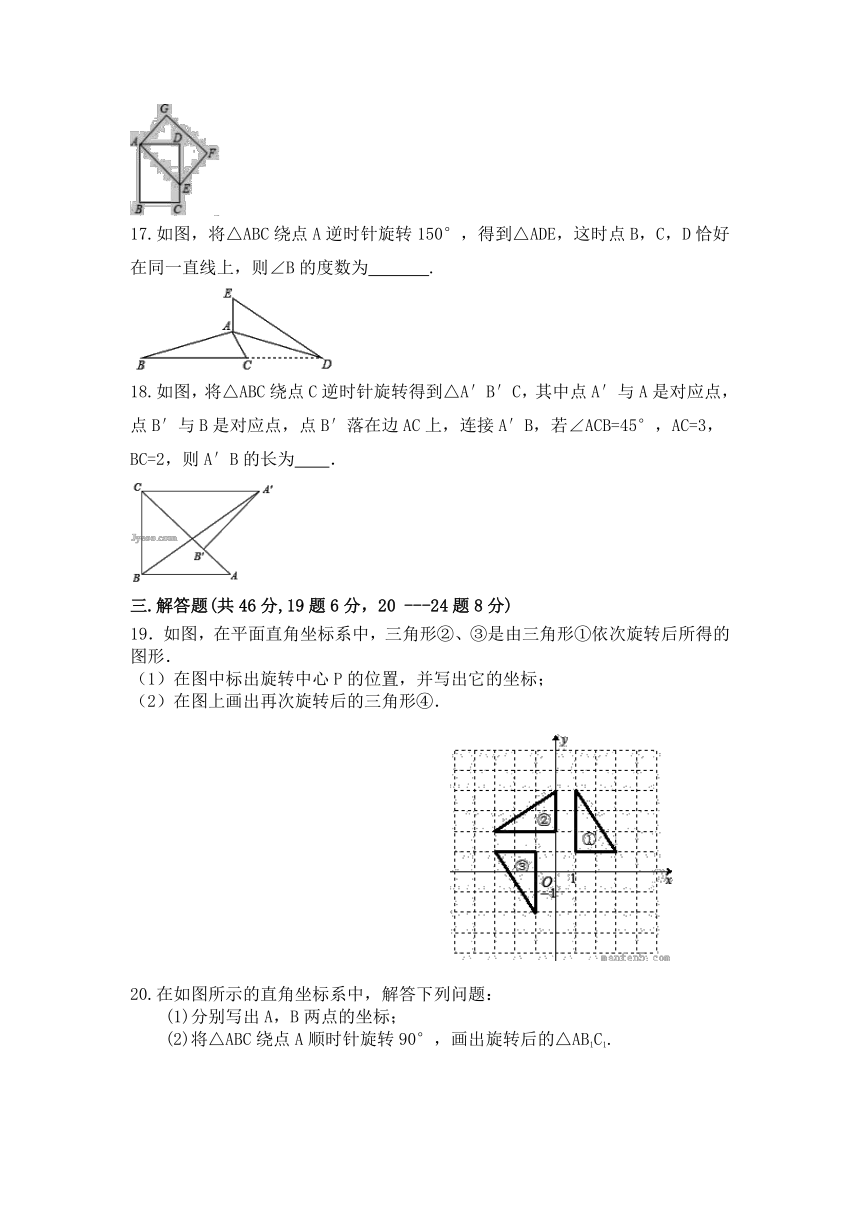
17.如图,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B,C,D恰好在同一直线上,则∠B的度数为 .
18.如图,将△ABC绕点C逆时针旋转得到△A′B′C,其中点A′与A是对应点,点B′与B是对应点,点B′落在边AC上,连接A′B,若∠ACB=45°,AC=3,BC=2,则A′B的长为 .
三.解答题(共46分,19题6分,20 ---24题8分)
19.如图,在平面直角坐标系中,三角形②、③是由三角形①依次旋转后所得的图形.
(1)在图中标出旋转中心P的位置,并写出它的坐标;
(2)在图上画出再次旋转后的三角形④.
20.在如图所示的直角坐标系中,解答下列问题:
(1)分别写出A,B两点的坐标;
(2)将△ABC绕点A顺时针旋转90°,画出旋转后的△AB1C1.
21.如图,四边形ABCD是正方形,△ADF绕着点A顺时旋转90°得到△ABE,若AF=4,AB=7.
(1)求DE的长度;
(2)指出BE与DF的关系如何?并说明由.
22.如图,已知:如图点,点在轴正半轴上,且,将线段绕点沿顺时针旋转,设点旋转后的对应点是点,求点的坐标.
23.已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
(1) 如图18, 连接DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请说明理由,若不正确请举反例说明;
(2) 若将正方形AEFG绕点A按顺时针方向旋转, 连接DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图19为例说明理由.
(
图
19
) (
图
18
)
24.将一张透明的平行四边形胶片沿对角线剪开,得到图①中的两张三角形胶片和.将这两张三角形胶片的顶点与顶点重合,把绕点顺时针方向旋转,这时与相交于点.
(
C
A
E
F
D
B
C
D
O
A
F
B
(
E
)
A
D
O
F
C
B
(
E
)
图
①
图
②
图
③
)
(1)当旋转至如图②位置,点,在同一直线上时,与的数量关系是 .
(2)当继续旋转至如图③位置时,题(1)中的结论还成立吗?请说明理由.
(3)在图③中,连接,探索与之间有怎样的位置关系,并证明.
参考答案
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D D C D B C C B
二、填空题(每题3分,共24分)
11.答案为:0.
12.答案为:4
13.答案为:y=-(x-2)2+1
14.【答案】
15. (-2-a,-b)或(2-a,-b)
16.答案为:3
17.答案为:15°.
18.答案为:.
三.解答题(共46分,19题6分,20 ---24题8分)
19.解答:解:(1)旋转中心点P位置如图所示,(2分)
点P的坐标为(0,1);(4分)
(2)旋转后的三角形④如图所示.(8分)
20.解:(1)由点A、B在坐标系中的位置可知:A(2,0),B(-1,-4);
(2)如图所示:2)如图所示:
21.(1)3;(2)BE=DF,BE⊥DF.
【详解】
解:(1)∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴AE=AF=4,AD=AB=7,
∴DE=AD﹣AE=7﹣4=3;
(2)BE、DF的关系为:BE=DF,BE⊥DF.理由如下:
∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
∵∠ADF+∠F=180°﹣90°=90°,
∴∠ABE+∠F=90°,
∴BE⊥DF,
∴BE、DF的关系为:BE=DF,BE⊥DF.
22.点的坐标为.
【详解】
解:如图,作轴于,
∵,,
∴,
∵线段绕点沿逆时针旋转得,
∴,且,
∴
而,
∴,
在和中
,
∴,
∴,,
∴,
∴点的坐标为.
23.解:(1)不相等,用图19即可说明;
(2)BE=DG。理由:连接BE,在△ADG和△ABE中,∵AD=AB,∠DAG=∠BAE,AG=AE,∴ADG≌ABE(SAS),∴BE=DG。
24.【解】(1)(或相等)
(2)(或成立),理由如下:
由,得
(或),.
,.
在和中,
.
.
,
.
(
A
D
O
F
C
B
(
E
)
G
)(3)如图,.
由,点与点重合,
得.
点在的垂直平分线上,
且.
,
,
.
,点在的垂直平分线上.
直线是的垂直平分线,.
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.下列说法正确的是( )
A.平移不改变图形的形状和大小,而旋转则改变图形的形状和大小
B.平移和旋转的共同点是改变图形的位置
C.图形可以向某方向平移一定距离,也可以向某方向旋转一定距离
D.由平移得到的图形也一定可由旋转得到
2.已知点的坐标为,为坐标原点,连结,将线段绕点按逆时针方向旋转得,则点的坐标为( )
A. B. C. D.
3.如图,在中,,在同一平面内,将绕点按逆时针方向旋转到的位置,使得,则
A. B. C. D.
4.若两个图形关于某一点成中心对称,那么下列说法.正确的是( )
①对称点的连线必过对称中心;②这两个图形一定全等;③对应线段一定平行(或在一条直线上)且相等;④将一个图形绕对称中心旋转必定与另一个图形重合.
A.①② B.①③ C.①②③ D.①②③④
5.如果一个图形绕着一个点至少需要旋转才能与它本身重合,则下列说法正确的是( )
A.这个图形一定是中心对称图形 B.这个图形可能是中心对称图形
C.这个图形旋转后能与它本身重合 D.以上都不对
6.同学们曾玩过万花筒,它是由三块等宽等长的玻璃围成的,图是看到的万花筒的一个图案,图中所有的小三角形均是全等的等边三角形,其中的菱形可以看成是把菱形以点为中心( ).
A.顺时针旋转得到 B.顺时针旋转得到
C.逆时针旋转得到 D.逆时针旋转得到
7. 如图,在平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点B′的坐标是( )
图7-ZT-1
A.(-1,2+) B.(-,3) C.(-,2+) D.(-3,)
8. 若点P(-a,a-3)关于原点对称的点是第二象限内的点,则a满足( )
A.a>3 B.0<a≤3
C.a<0 D.a<0或a>3
9. 如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为 ( )
A.4,30° B.2,60° C.1,30° D.3,60°
10. 在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取一定点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,-300°)或P(3,420°)等,则与点P关于点O对称的点Q的极坐标表示不正确的是( )
A.Q(3,240°) B.Q(3,-120°) C.Q(3,600°) D.Q(3,-500°)
二、填空题(每题3分,共24分)
11.点(a,2)与点(b,-2)关于原点中心对称,则a+b的值是 .
12.如图是4×4的正方形网格,再把其中一个白色小正方形涂上阴影,使整个阴影部分成为轴对称图形,这样的白色小正方形有________个.
13.如图,已知抛物线C1,抛物线C2关于原点对称.若抛物线C1的解析式为y=(x+2)2-1,那么抛物线C2的解析式为 .
14.如图,在平面直角坐标系中,将绕点旋转180°得到,则点的坐标为__________.
15. 已知 ABCD的顶点A在第三象限,对角线AC的中点在坐标原点,一边AB与x轴平行且AB=2.若点A的坐标为(a,b),则点D的坐标为________________.
16.如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为 .
17.如图,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B,C,D恰好在同一直线上,则∠B的度数为 .
18.如图,将△ABC绕点C逆时针旋转得到△A′B′C,其中点A′与A是对应点,点B′与B是对应点,点B′落在边AC上,连接A′B,若∠ACB=45°,AC=3,BC=2,则A′B的长为 .
三.解答题(共46分,19题6分,20 ---24题8分)
19.如图,在平面直角坐标系中,三角形②、③是由三角形①依次旋转后所得的图形.
(1)在图中标出旋转中心P的位置,并写出它的坐标;
(2)在图上画出再次旋转后的三角形④.
20.在如图所示的直角坐标系中,解答下列问题:
(1)分别写出A,B两点的坐标;
(2)将△ABC绕点A顺时针旋转90°,画出旋转后的△AB1C1.
21.如图,四边形ABCD是正方形,△ADF绕着点A顺时旋转90°得到△ABE,若AF=4,AB=7.
(1)求DE的长度;
(2)指出BE与DF的关系如何?并说明由.
22.如图,已知:如图点,点在轴正半轴上,且,将线段绕点沿顺时针旋转,设点旋转后的对应点是点,求点的坐标.
23.已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
(1) 如图18, 连接DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请说明理由,若不正确请举反例说明;
(2) 若将正方形AEFG绕点A按顺时针方向旋转, 连接DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图19为例说明理由.
(
图
19
) (
图
18
)
24.将一张透明的平行四边形胶片沿对角线剪开,得到图①中的两张三角形胶片和.将这两张三角形胶片的顶点与顶点重合,把绕点顺时针方向旋转,这时与相交于点.
(
C
A
E
F
D
B
C
D
O
A
F
B
(
E
)
A
D
O
F
C
B
(
E
)
图
①
图
②
图
③
)
(1)当旋转至如图②位置,点,在同一直线上时,与的数量关系是 .
(2)当继续旋转至如图③位置时,题(1)中的结论还成立吗?请说明理由.
(3)在图③中,连接,探索与之间有怎样的位置关系,并证明.
参考答案
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D D C D B C C B
二、填空题(每题3分,共24分)
11.答案为:0.
12.答案为:4
13.答案为:y=-(x-2)2+1
14.【答案】
15. (-2-a,-b)或(2-a,-b)
16.答案为:3
17.答案为:15°.
18.答案为:.
三.解答题(共46分,19题6分,20 ---24题8分)
19.解答:解:(1)旋转中心点P位置如图所示,(2分)
点P的坐标为(0,1);(4分)
(2)旋转后的三角形④如图所示.(8分)
20.解:(1)由点A、B在坐标系中的位置可知:A(2,0),B(-1,-4);
(2)如图所示:2)如图所示:
21.(1)3;(2)BE=DF,BE⊥DF.
【详解】
解:(1)∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴AE=AF=4,AD=AB=7,
∴DE=AD﹣AE=7﹣4=3;
(2)BE、DF的关系为:BE=DF,BE⊥DF.理由如下:
∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
∵∠ADF+∠F=180°﹣90°=90°,
∴∠ABE+∠F=90°,
∴BE⊥DF,
∴BE、DF的关系为:BE=DF,BE⊥DF.
22.点的坐标为.
【详解】
解:如图,作轴于,
∵,,
∴,
∵线段绕点沿逆时针旋转得,
∴,且,
∴
而,
∴,
在和中
,
∴,
∴,,
∴,
∴点的坐标为.
23.解:(1)不相等,用图19即可说明;
(2)BE=DG。理由:连接BE,在△ADG和△ABE中,∵AD=AB,∠DAG=∠BAE,AG=AE,∴ADG≌ABE(SAS),∴BE=DG。
24.【解】(1)(或相等)
(2)(或成立),理由如下:
由,得
(或),.
,.
在和中,
.
.
,
.
(
A
D
O
F
C
B
(
E
)
G
)(3)如图,.
由,点与点重合,
得.
点在的垂直平分线上,
且.
,
,
.
,点在的垂直平分线上.
直线是的垂直平分线,.
同课章节目录
