正余弦定理的应用[上学期]

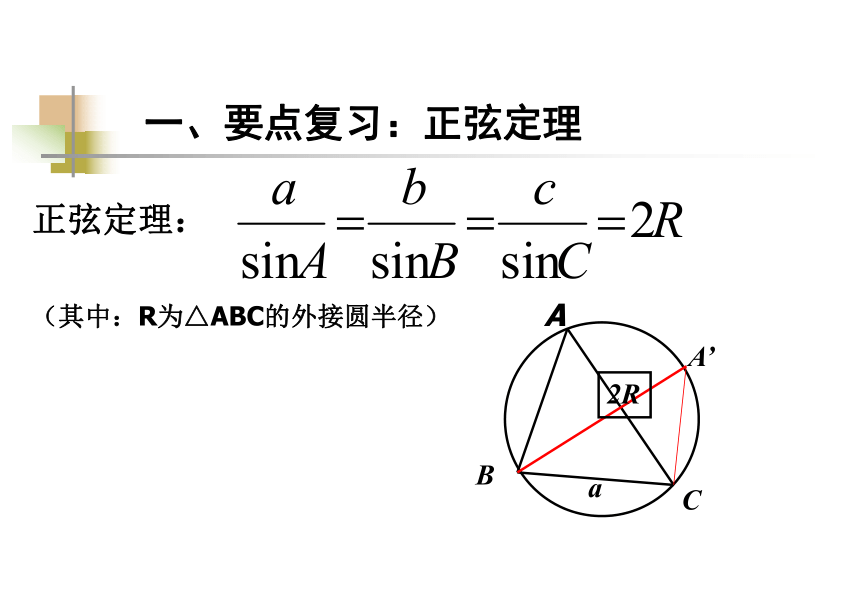
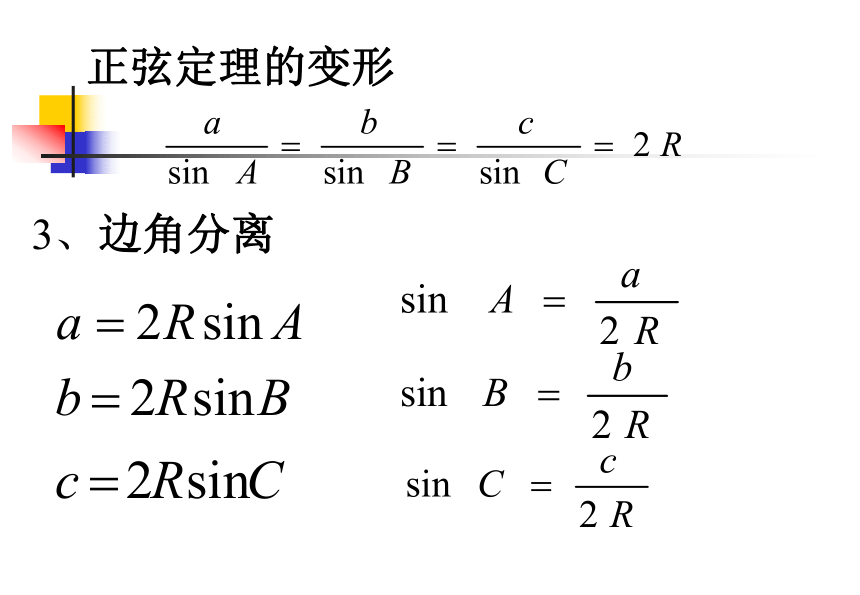
课件16张PPT。正余弦定理的应用一、要点复习：正弦定理BCaA二、正弦定理的变形 1,正弦定理的变形3、边角分离4，5, a:b:c=sinA:sinB:sinC正弦定理的变形 1，面积三、三角形的面积及常用关系式 (1) (2) (3)r为△内切圆半径 2,常用关系式 (1)A+B+C=π (2) sin(A+B)=sinC cos(A+B)=－cosC (3) 四、正弦定理应用（1）已知两角和任意一边
（2） 已知两边和其一对角 BCAabc例题讲解例题讲解∴ A 为锐角 例题讲解 在?ABC中，已知2b=a+c，证明：
2sinB=sinA+sinC问题1：引：能找到三角形各边与对角正弦的关系吗？导：如何利用正弦定理证明以上关系？ 证明：由 得 即 2sinB=sinA+sinCa=2RsinA，b=2RsinB，c=2RsinC， 将此式 代入 2b=a+c 得2?2RsinB=2RsinA+2RsinC灵活运用变式1：a=2RsinA，b=2RsinB，c=2RsinC， 变式2： 在?ABC中，已知bcosA=acosB，
判断三角形的形状。 解：由 得 a=2RsinA，b=2RsinB， 将此式 代入bcosA=acosB 得（2RsinB）cosA=（2RsinA）cosBsinAcosB - cosAsinB=0 ,Sin(A – B) =0由-?（a+b+c)(b+c-a)=3bc,且sin2A=sinBcosC,
判断三角形的形状。