余弦定理2[上学期]
图片预览



文档简介
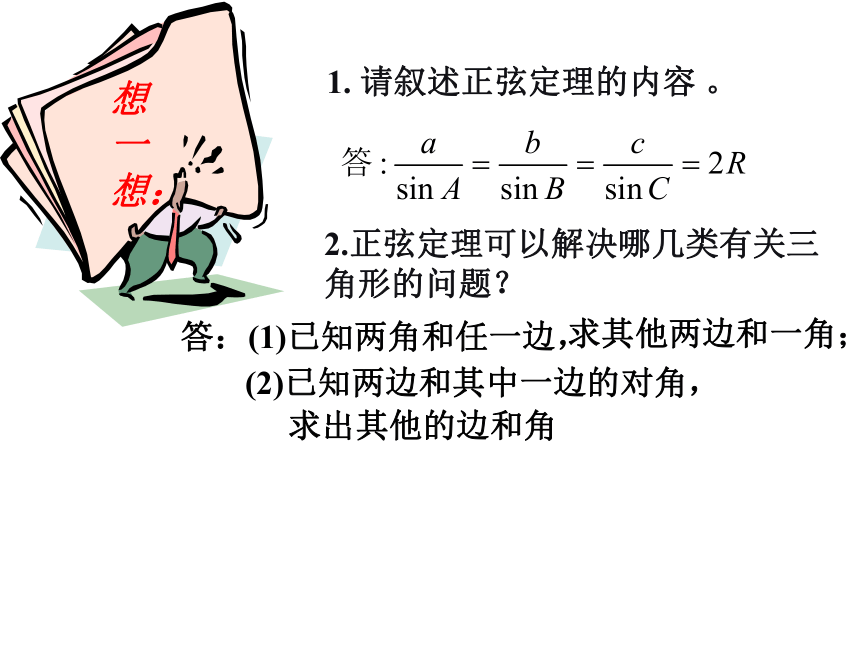
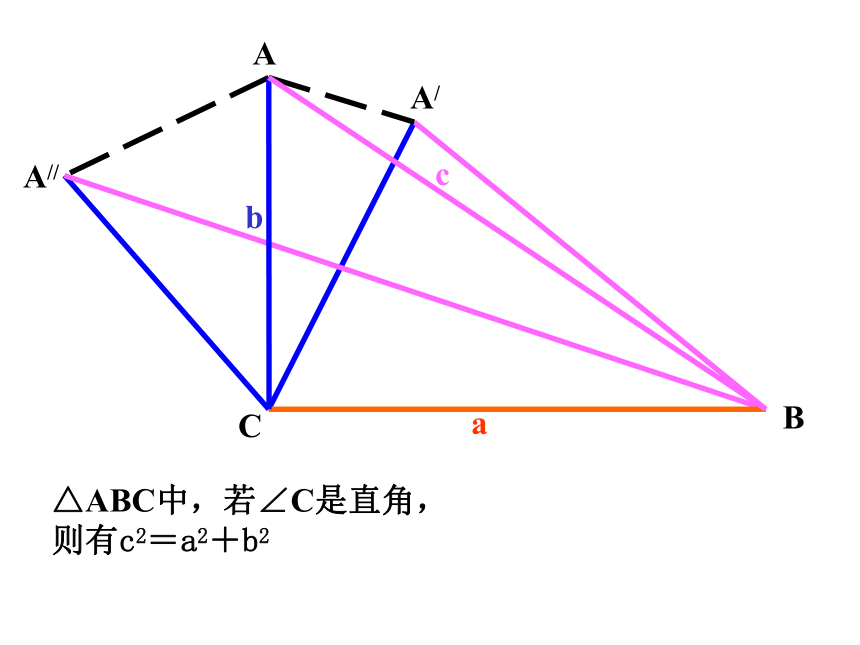
课件11张PPT。余弦定理 1. 请叙述正弦定理的内容 。答:(1)已知两角和任一边, 2.正弦定理可以解决哪几类有关三角形的问题? 求其他两边和一角; (2)已知两边和其中一边的对角, 求出其他的边和角 △ABC中,若∠C是直角,
则有c2=a2+b2 A/A//如图:ΔABC中,AB,BC,CA的长分别为c,a,b =c2-2ac cosB+a2即:b2=c2-2ac cosB+a2同理可证:a2=b2+c2-2bc cosA
c2=a2+b2-2ab cosC余弦定理:三角形任何一边的平方等于其它两边平方的和减去这两边与它们夹角的余弦的积的两倍。
即:a2=b2+c2-2bc cosA
b2=a2+c2-2ac cosB
c2=a2+b2-2ab cosC注意:1、熟悉定理的形式结构特点,注意“平方”“夹角”“余弦”等 2、每个等式中包含四个量,它们分别是三角形的三条边和其中一角,知三求一 3、当∠C=90?时,则cosC=0,∴c2=a2+b2,即余弦定理是勾股定理的推广,勾股定理是余弦定理的特例余弦定理:三角形任何一边的平方等于其它两边平方的 和减去这两边与它们夹角的余弦的积的两倍。
即:a2=b2+c2-2bc cosA
b2=a2+c2-2ac cosB
c2=a2+b2-2ab cosC
公式变形:问:利用余弦定理可以解决那几类有关三角形的问题呢?例 1:在?ABC中,已知a=7,b=10, c=6,求A、B和C.解:∴ A≈44°∴ C≈36°∴ B=180°-(A+C)≈100°.已知三边,求三角=0.725,=0.8071,解:∴B=135° ∴ A= 180°-(B+C) = 30° 已知两边和它们的夹角,求另一边和另两角 注:解决这类问题可有两种方法:
(1)正弦定理(2)利用方程的思想,引出含第三边为未知量的方程, 间接利用余弦定理解决问题已知两边和其中一边对角,求另一边及另两角 练习:
课本P133 练习31.余弦定理:三角形任何一边的平方等于其它两边平方的 和减去这两边与它们夹角的余弦的积的两倍。
即:a2=b2+c2-2bc cosA
b2=a2+c2-2ac cosB
c2=a2+b2-2ab cosC
公式变形:2.利用余弦定理可以解决那些有关三角形的问题呢?(1)已知三边,求三角(2)已知两边和它们的夹角,求另一边和另两角 (3)已知两边和其中一边对角,求另一边及另两角 小结:1.余弦定理的内容
2.余弦定理可以解决那几类有关三角形的问题?
则有c2=a2+b2 A/A//如图:ΔABC中,AB,BC,CA的长分别为c,a,b =c2-2ac cosB+a2即:b2=c2-2ac cosB+a2同理可证:a2=b2+c2-2bc cosA
c2=a2+b2-2ab cosC余弦定理:三角形任何一边的平方等于其它两边平方的和减去这两边与它们夹角的余弦的积的两倍。
即:a2=b2+c2-2bc cosA
b2=a2+c2-2ac cosB
c2=a2+b2-2ab cosC注意:1、熟悉定理的形式结构特点,注意“平方”“夹角”“余弦”等 2、每个等式中包含四个量,它们分别是三角形的三条边和其中一角,知三求一 3、当∠C=90?时,则cosC=0,∴c2=a2+b2,即余弦定理是勾股定理的推广,勾股定理是余弦定理的特例余弦定理:三角形任何一边的平方等于其它两边平方的 和减去这两边与它们夹角的余弦的积的两倍。
即:a2=b2+c2-2bc cosA
b2=a2+c2-2ac cosB
c2=a2+b2-2ab cosC
公式变形:问:利用余弦定理可以解决那几类有关三角形的问题呢?例 1:在?ABC中,已知a=7,b=10, c=6,求A、B和C.解:∴ A≈44°∴ C≈36°∴ B=180°-(A+C)≈100°.已知三边,求三角=0.725,=0.8071,解:∴B=135° ∴ A= 180°-(B+C) = 30° 已知两边和它们的夹角,求另一边和另两角 注:解决这类问题可有两种方法:
(1)正弦定理(2)利用方程的思想,引出含第三边为未知量的方程, 间接利用余弦定理解决问题已知两边和其中一边对角,求另一边及另两角 练习:
课本P133 练习31.余弦定理:三角形任何一边的平方等于其它两边平方的 和减去这两边与它们夹角的余弦的积的两倍。
即:a2=b2+c2-2bc cosA
b2=a2+c2-2ac cosB
c2=a2+b2-2ab cosC
公式变形:2.利用余弦定理可以解决那些有关三角形的问题呢?(1)已知三边,求三角(2)已知两边和它们的夹角,求另一边和另两角 (3)已知两边和其中一边对角,求另一边及另两角 小结:1.余弦定理的内容
2.余弦定理可以解决那几类有关三角形的问题?
