余弦定理1（高）[下学期]

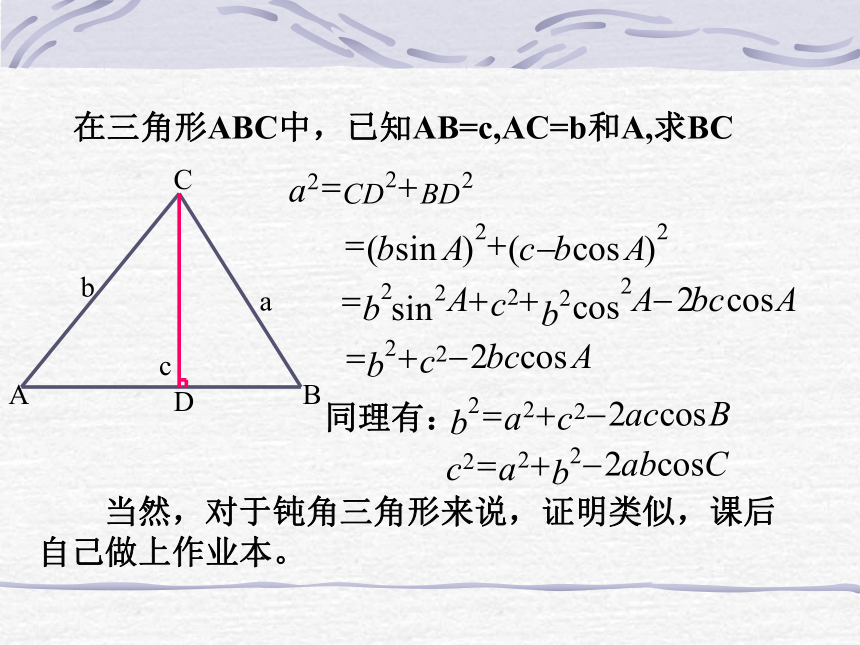
课件12张PPT。用正弦定理解三角形需要已知哪些条件？ 已知三角形的两角和一边，或者是已知两边和其中一边的对角。 那么，如果在一个三角形（非直角三角形）中，已知两边及这两边的夹角(非直角），能否用正弦定理解这个三角形，为什么？复习回顾余弦定理 余弦定理作为勾股定理的推广，那么我们可以借助勾股定理来证明余弦定理。在三角形ABC中，已知AB=c,AC=b和A,求BC 当然，对于钝角三角形来说，证明类似，课后 自己做上作业本。那么，学过向量之后，能否用向量的方法给予证明呢？已知AB,AC和它们的夹角A，求CB用语言描述：三角形任何一边的平方等于其它两边的平方和, 再减去这两边与它们夹角的余弦的积的两倍。它还有别的用途么，若已知a,b,c,可以求什么？归纳：
利用余弦定理可以解决以下两类有关三角形的问题： （1）已知三边，求三个角 （2）已知两边和它们的夹角，求第三边，进而还可求其它两个角。分析：已知三边，求三个角，可用余弦定理的变形来解决问题思考：已知条件不变，将例1稍做改动
（1）在三角形ABC中，已知a=7,b=10,c=6,判定三角形ABC的形状分析：三角形ABC的形状是由大边b所对的大角B决定的。（2）在三角形ABC中，已知a=7,b=10,c=6,求三角形ABC的面积分析：已知两边和两边的夹角总结（1）余弦定理适用于任何三角形（3）由余弦定理可知：（2）余弦定理的作用： a、已知三边，求三个角 b、已知两边及这两边的夹角，求第三边，进而可求出其它两个角c、判断三角形的形状，求三角形的面积例4：一钝角三角形的边长为连续自然数，则这三边长为（ ）
A、1，2，3 B、2，3，4 C、3，4，5 D、4，5，6分析： 要看哪一组符合要求，只需检验哪一个选项
中的最大角是钝角，即该角的余弦值小于0。A、C显然不满足B分析：求最大角的余弦值，最主要的是判断哪个角是最大角。由大边对大角，已知两边可求出第三边,找到最大角。则有：b是最大边，那么B 是最大角