余弦定理[下学期]
图片预览




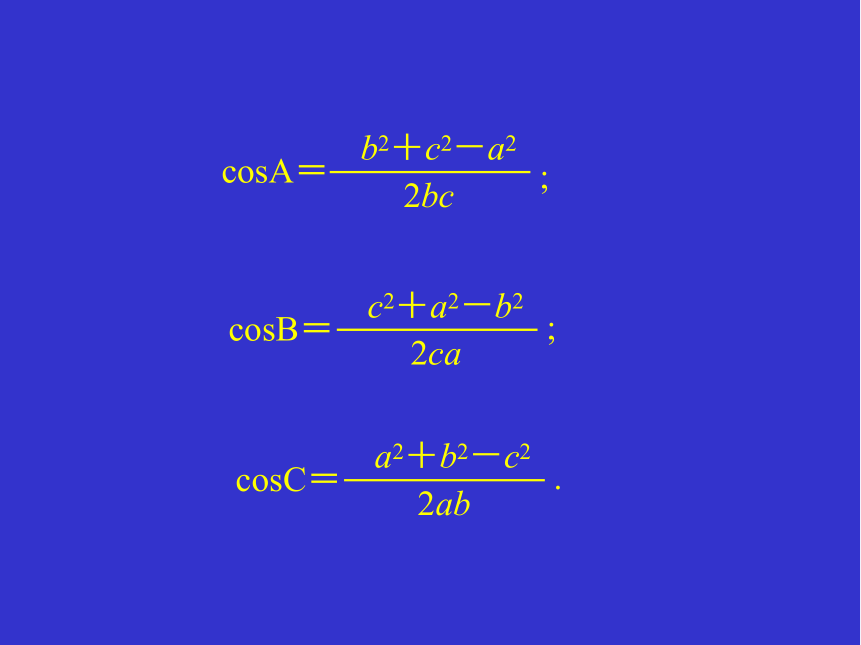

文档简介
(共19张PPT)
高一数学
课题 余弦定理
授课人:肖俊妮
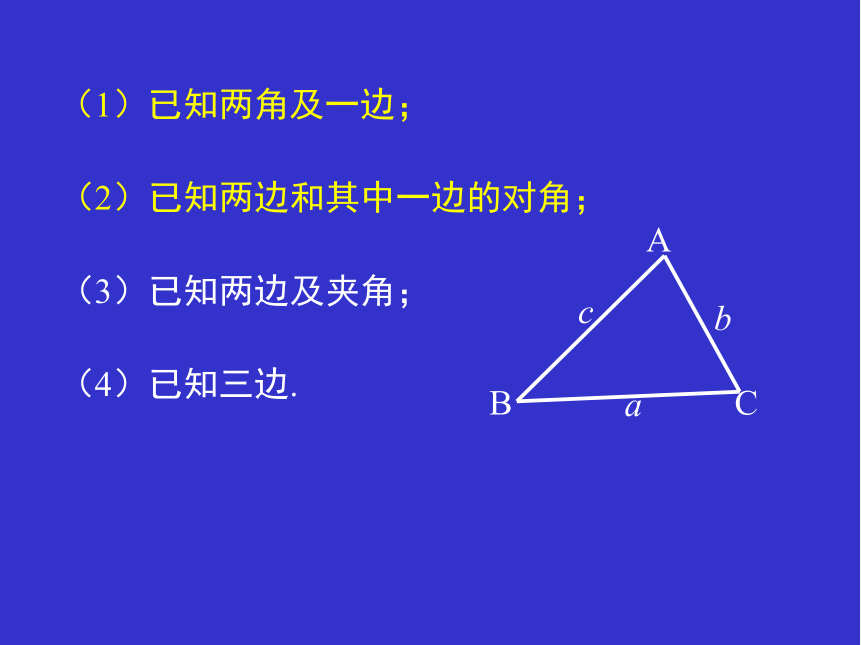
(1)已知两角及一边;
(2)已知两边和其中一边的对角;
(3)已知两边及夹角;
(4)已知三边.
A
B
C
a
b
c
2. 余弦定理
∵ a-b=c,
∴ (a-b)·(a-b)=c·c ,
∴ |a|2 +|b|2 -2a·b=|c|2,
即 c2=a2+b2-2abcosC.
A
B
C
a
b
c
c2=a2+b2-2abcosC;
b2=c2+a2-2cacosB;
a2=b2+c2-2bccosA.
余弦定理:三角形任何一边的平方等于其
他两边平方的和减去这两边与
它们夹角的余弦的积的两倍.
b2+c2-a2
2bc
cosA=
c2+a2-b2
2ca
cosB=
a2+b2-c2
2ab
cosC=
;
;
.
利用余弦定理,可以解决:
(1)已知三边,求三个角;
(2)已知两边及夹角,求第三边和
其他两个角.
A
B
C
a
b
c
c2=a2+b2-2abcosC.
a2+b2-c2
2ab
cosC=
例 1:在 ABC中,已知a=7,b=10,
c=6,求A、B和C.
解:
b2+c2-a2
2bc
∵ cosA= =0.725,
∴ A≈44°
a2+b2-c2
2ab
∵ cosC= =0.8071,
∴ C≈36°,
∴ B=180°-(A+C)≈100°.
∵sinC= ≈0.5954,
∴ C ≈ 36°或144°(舍).
c sinA
a
(
)
例 2:在 ABC中,已知a=2.730,b=3.696,
C=82°28′,解这个三角形.
解:
由 c2=a2+b2-2abcosC,
得 c≈4.297.
b2+c2-a2
2bc
∵ cosA= ≈0.7767,
∴ A≈39°2′,
∴ B=180°-(A+C)=58°30′.
a sinC
c
∵sinA= ≈0.6299,
∴ A=39°或141°(舍).
(
)
解:
在 AOB中,
∵ |a – b|2 = |a|2+|b| 2 – 2|a||b|cos120°
=61,
∴ |a – b|=√61.
例 4:已知向量a、b夹角为120°,
且|a| =5,|b|=4,求|a – b| 、
|a+b| 及a+b与a的夹角.
a-b
a+b
B
b
A
C
a
120°
O
∴ a+b =√21.
∴ ∠COA即a+b与a的夹角约为49°.
∵ cos∠COA= ≈0.6546,
a 2+ a+b 2 – b 2
2 a a+b
例 4:已知向量a、b夹角为120°,
且|a| =5,|b|=4,求|a – b| 、
|a+b| 及a+b与a的夹角.
a-b
a+b
B
b
A
C
a
120°
O
在 OAC中,
∵ |a + b|2 = |a|2+|b| 2 – 2|a||b|cos60°
=21,
例5 已知四边形ABCD的四边长为AB = 2.4, BC = CD = DA = 1, A= 30°, 求C.
解: BD2 = AB2 + AD2 – 2AB·ADcosA
≈ 2.60,
cosC = = – 0.30,
DC2 + BC2 – BD2
2DC·BC
A
30°
D
C
B
C ≈ 107.5°.
思考:若A= θ, 怎样用θ表示四边形ABCD的面积?
练习
ABC中,
(1)a=4,b=3,C=60°,则c=_____;
√13
14.6°
(2)a = 2, b = 3, c = 4, 则C = ______.
104.5°
(3)a=2,b=4,C=135°,则A=______.
小结
1.余弦定理是解三角形的又一重要工具
c2=a2+b2-2abcosC;
b2=c2+a2-2cacosB;
a2=b2+c2-2bccosA;
b2+c2-a2
2bc
cosA=
c2+a2-b2
2ca
cosB=
a2+b2-c2
2ab
cosC=
2.余弦定理可解以下两种类型的三角形:
(1)已知三边;
(2)已知两边及夹角.
;
;
.
今日作业
P131 练习
第3、4题;
习题5.9
第6、7题.
研究题
总结解三角形的方法:已知三角形边角中哪三个量,有唯一解或多解或无解?分别用什么方法?
高一数学
课题 余弦定理
授课人:肖俊妮
(1)已知两角及一边;
(2)已知两边和其中一边的对角;
(3)已知两边及夹角;
(4)已知三边.
A
B
C
a
b
c
2. 余弦定理
∵ a-b=c,
∴ (a-b)·(a-b)=c·c ,
∴ |a|2 +|b|2 -2a·b=|c|2,
即 c2=a2+b2-2abcosC.
A
B
C
a
b
c
c2=a2+b2-2abcosC;
b2=c2+a2-2cacosB;
a2=b2+c2-2bccosA.
余弦定理:三角形任何一边的平方等于其
他两边平方的和减去这两边与
它们夹角的余弦的积的两倍.
b2+c2-a2
2bc
cosA=
c2+a2-b2
2ca
cosB=
a2+b2-c2
2ab
cosC=
;
;
.
利用余弦定理,可以解决:
(1)已知三边,求三个角;
(2)已知两边及夹角,求第三边和
其他两个角.
A
B
C
a
b
c
c2=a2+b2-2abcosC.
a2+b2-c2
2ab
cosC=
例 1:在 ABC中,已知a=7,b=10,
c=6,求A、B和C.
解:
b2+c2-a2
2bc
∵ cosA= =0.725,
∴ A≈44°
a2+b2-c2
2ab
∵ cosC= =0.8071,
∴ C≈36°,
∴ B=180°-(A+C)≈100°.
∵sinC= ≈0.5954,
∴ C ≈ 36°或144°(舍).
c sinA
a
(
)
例 2:在 ABC中,已知a=2.730,b=3.696,
C=82°28′,解这个三角形.
解:
由 c2=a2+b2-2abcosC,
得 c≈4.297.
b2+c2-a2
2bc
∵ cosA= ≈0.7767,
∴ A≈39°2′,
∴ B=180°-(A+C)=58°30′.
a sinC
c
∵sinA= ≈0.6299,
∴ A=39°或141°(舍).
(
)
解:
在 AOB中,
∵ |a – b|2 = |a|2+|b| 2 – 2|a||b|cos120°
=61,
∴ |a – b|=√61.
例 4:已知向量a、b夹角为120°,
且|a| =5,|b|=4,求|a – b| 、
|a+b| 及a+b与a的夹角.
a-b
a+b
B
b
A
C
a
120°
O
∴ a+b =√21.
∴ ∠COA即a+b与a的夹角约为49°.
∵ cos∠COA= ≈0.6546,
a 2+ a+b 2 – b 2
2 a a+b
例 4:已知向量a、b夹角为120°,
且|a| =5,|b|=4,求|a – b| 、
|a+b| 及a+b与a的夹角.
a-b
a+b
B
b
A
C
a
120°
O
在 OAC中,
∵ |a + b|2 = |a|2+|b| 2 – 2|a||b|cos60°
=21,
例5 已知四边形ABCD的四边长为AB = 2.4, BC = CD = DA = 1, A= 30°, 求C.
解: BD2 = AB2 + AD2 – 2AB·ADcosA
≈ 2.60,
cosC = = – 0.30,
DC2 + BC2 – BD2
2DC·BC
A
30°
D
C
B
C ≈ 107.5°.
思考:若A= θ, 怎样用θ表示四边形ABCD的面积?
练习
ABC中,
(1)a=4,b=3,C=60°,则c=_____;
√13
14.6°
(2)a = 2, b = 3, c = 4, 则C = ______.
104.5°
(3)a=2,b=4,C=135°,则A=______.
小结
1.余弦定理是解三角形的又一重要工具
c2=a2+b2-2abcosC;
b2=c2+a2-2cacosB;
a2=b2+c2-2bccosA;
b2+c2-a2
2bc
cosA=
c2+a2-b2
2ca
cosB=
a2+b2-c2
2ab
cosC=
2.余弦定理可解以下两种类型的三角形:
(1)已知三边;
(2)已知两边及夹角.
;
;
.
今日作业
P131 练习
第3、4题;
习题5.9
第6、7题.
研究题
总结解三角形的方法:已知三角形边角中哪三个量,有唯一解或多解或无解?分别用什么方法?
