余弦定理[下学期]
图片预览


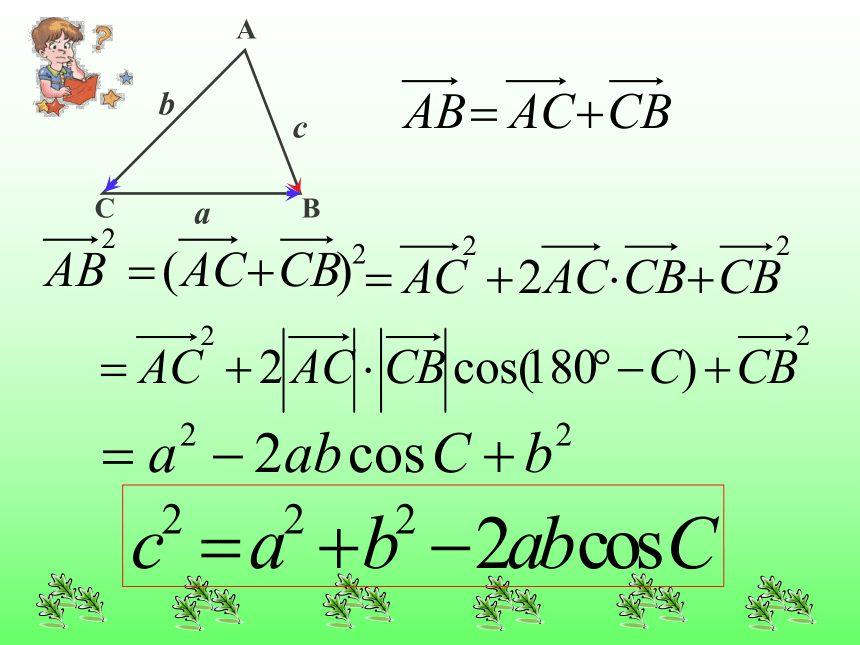

文档简介
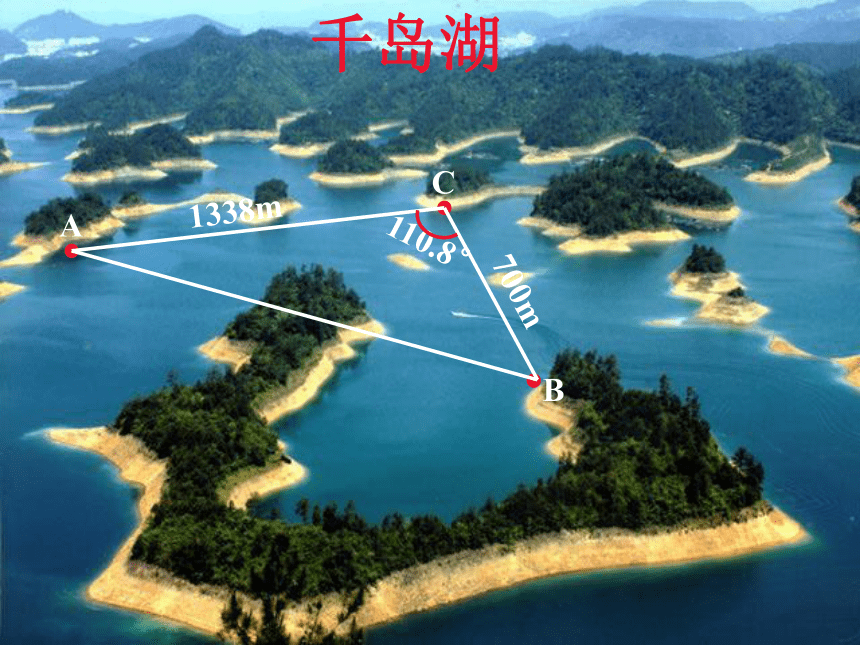
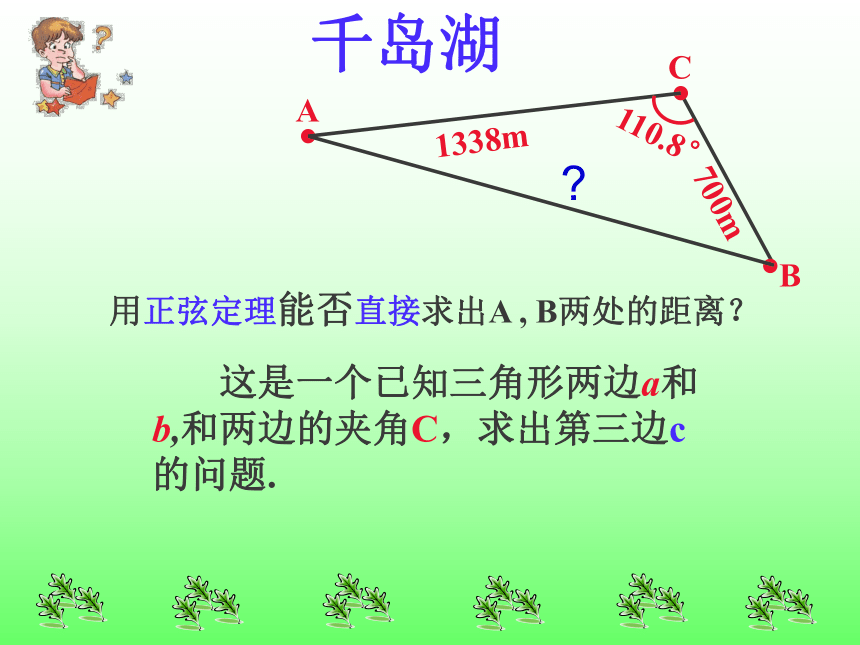
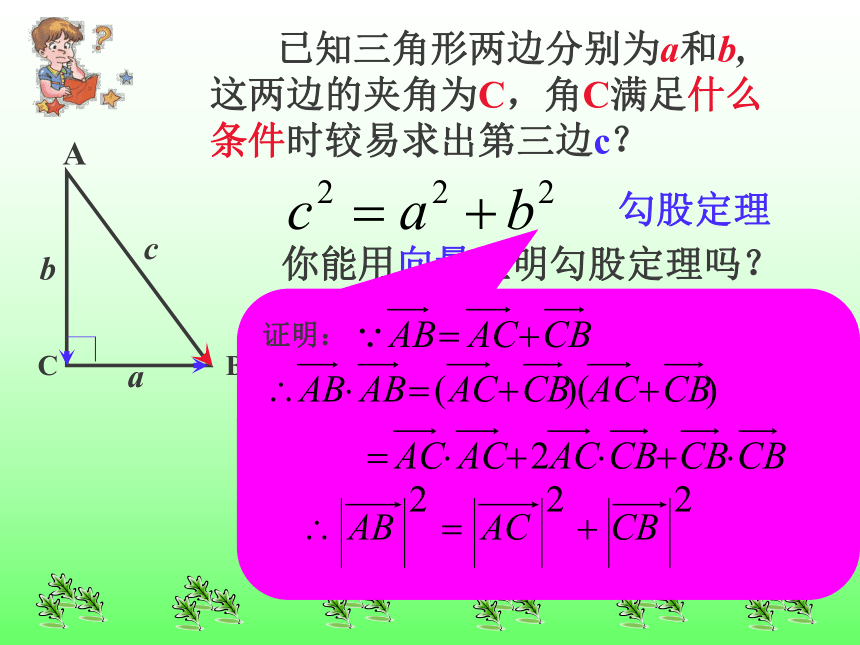
课件14张PPT。余弦定理2、正弦定理可以解哪几类的三角形问题? (1)已知两角和任一边,求其他两边和一角;(2)已知两边和其中一边的对角,求另一边的对角(进而求出其他的边和角)。1、正弦定理第二种情况若知道的是大边的对角,只有唯一的一组解;若给出的是小边的对角,则结果可能是两解或一解、或无 解.3、向量的数量积:千岛湖 110.8° 700m1338m千岛湖 用正弦定理能否直接求出A , B两处的距离? 这是一个已知三角形两边a和b,和两边的夹角C,求出第三边c的问题.? 已知三角形两边分别为a和b,这两边的夹角为C,角C满足什么条件时较易求出第三边c?勾股定理你能用向量证明勾股定理吗?证明: 余弦定理
三角形任何一边的平方等于其他两边的平方和减去这两边与它们夹角的余弦的积的两倍。勾股定理令C=900勾股定理与余弦定理有何关系?公式的结构特征怎样?这个定理有什么作用?它还有别的用途吗,
若已知a,b,c,可以求什么?利用余弦定理可以解决以下两类有关三角形的问题: (1)已知三边,求三个角 ; (2)已知两边和它们的夹角,求第三边,进而还可求其它两个角。归纳:思考:已知条件不变,将例1稍做改动
(1)在三角形ABC中,已知a=7,b=10,c=6,判定三角形ABC的形状例题千岛湖 ?答:A , B两处的距离约为1716米。(精确到1米)总结(1)余弦定理适用于任何三角形(3)由余弦定理可知:(2)余弦定理的作用: a、已知三边,求三个角 b、已知两边及这两边的夹角,求第三边,进而可求出其它两个角c、判断三角形的形状分析:求最大角的余弦值,最主要的是判断哪个角是最大角。由大边对大角,已知两边可求出第三边,找到最大角。解:则有:b是最大边,那么B 是最大角例4:一钝角三角形的边长为连续自然数,则这三边长为( )
A、1,2,3 B、2,3,4 C、3,4,5 D、4,5,6分析: 要看哪一组符合要求,只需检验哪一个选项
中的最大角是钝角,即该角的余弦值小于0。A、C显然不满足B练习:
三角形任何一边的平方等于其他两边的平方和减去这两边与它们夹角的余弦的积的两倍。勾股定理令C=900勾股定理与余弦定理有何关系?公式的结构特征怎样?这个定理有什么作用?它还有别的用途吗,
若已知a,b,c,可以求什么?利用余弦定理可以解决以下两类有关三角形的问题: (1)已知三边,求三个角 ; (2)已知两边和它们的夹角,求第三边,进而还可求其它两个角。归纳:思考:已知条件不变,将例1稍做改动
(1)在三角形ABC中,已知a=7,b=10,c=6,判定三角形ABC的形状例题千岛湖 ?答:A , B两处的距离约为1716米。(精确到1米)总结(1)余弦定理适用于任何三角形(3)由余弦定理可知:(2)余弦定理的作用: a、已知三边,求三个角 b、已知两边及这两边的夹角,求第三边,进而可求出其它两个角c、判断三角形的形状分析:求最大角的余弦值,最主要的是判断哪个角是最大角。由大边对大角,已知两边可求出第三边,找到最大角。解:则有:b是最大边,那么B 是最大角例4:一钝角三角形的边长为连续自然数,则这三边长为( )
A、1,2,3 B、2,3,4 C、3,4,5 D、4,5,6分析: 要看哪一组符合要求,只需检验哪一个选项
中的最大角是钝角,即该角的余弦值小于0。A、C显然不满足B练习:
