2022—2023学年人教版数学八年级上册11.3.2 多边形的内角和 课件 (共18张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册11.3.2 多边形的内角和 课件 (共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 134.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-08 09:58:15 | ||
图片预览




文档简介
(共18张PPT)
11.3.2 多边形的内角和
第十一章 三角形
11.3 多边形及其内角和
璧山区正则中学 薛霁
问题2 你知道长方形和正方形的内角和是多少 度?
问题1 三角形内角和是多少度?
问题3 猜想任意四边形的内角和是多少度?
探究一 多边形的内角和
猜想与证明
A
B
C
D
将四边形转化为两个三角形
猜想:四边形ABCD的内角和是360°
问题4 你能用以前学过的知识说明一下你的结论吗?
A
C
D
E
B
A
B
C
D
E
F
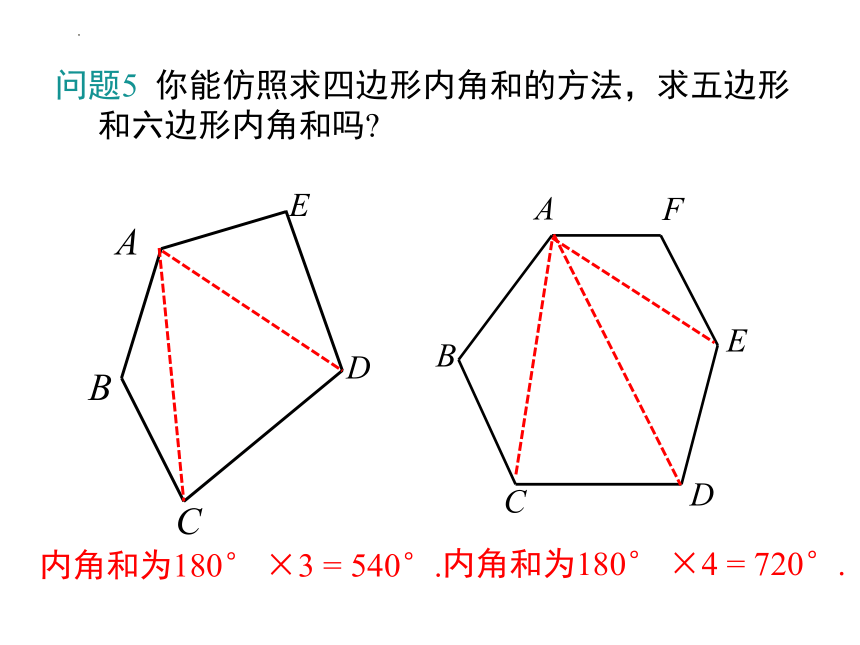
问题5 你能仿照求四边形内角和的方法,求五边形和六边形内角和吗
内角和为180° ×3 = 540°.
内角和为180° ×4 = 720°.
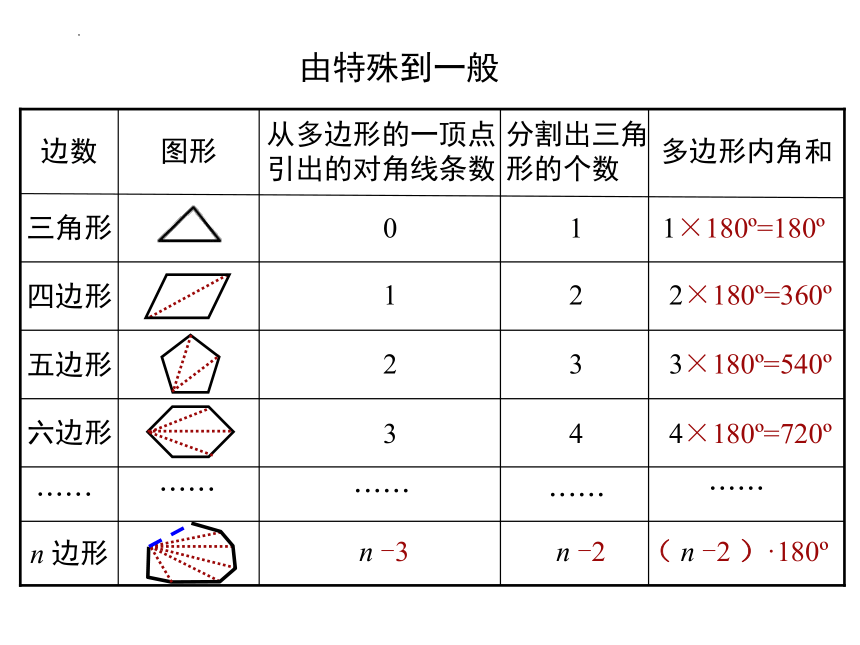
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一顶点引出的对角线条数
图形
边数
······
0
n -3
1
2
3
1
2
3
4
n -2
( n -2 )·180
1×180 =180
2×180 =360
3×180 =540
4×180 =720
······
······
······
······
由特殊到一般
多边形
三角形
转化思想
总结归纳
多边形的内角和公式
n边形内角和等于(n-2)×180 °.
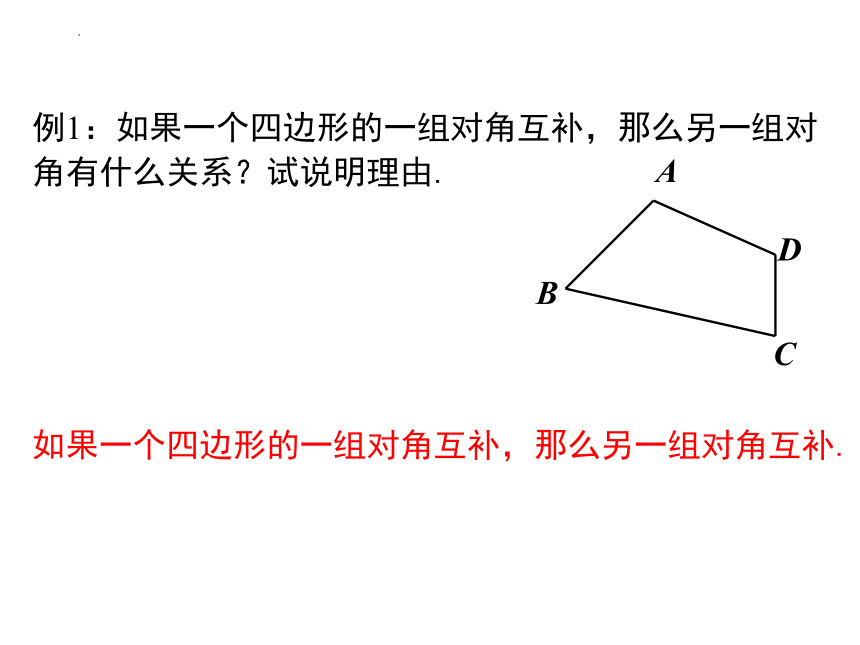
例1:如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.
A
B
C
D
如果一个四边形的一组对角互补,那么另一组对角互补.
【变式题】如图,在四边形ABCD中,∠A与∠C互补,BE平分∠ABC,DF平分∠ADC,若BE∥DF,求证:△DCF为直角三角形.
例2 一个多边形的内角和比四边形的内角和多720°,并且这个多边形的各内角都相等,这个多边形的每个内角是多少度?
探究三 多边形的外角和
如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.
问题1:任意一个外角和它相邻的内角有什么关系?
问题2:五个外角加上它们分别相邻的五个内角和是多少?
问题3:这五个平角和与五边形的内角和、外角和有什么关系?
E
B
C
D
1
2
3
4
5
A
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
n边形的外角和等于360°.
-(n-2) × 180°
=360 °
=n个平角-n边形内角和
= n×180 °
An
A2
A3
A4
1
2
3
4
n
A1
思考:n边形的外角和又是多少呢?
与边数无关
问题4:回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?为什么?
每个内角的度数是
每个外角的度数是
课堂练习:书24页练习题1、2、3
例3 已知一个多边形,它的内角和等于外角和的
2倍,求这个多边形的边数.
例4 已知一个多边形的每个内角与外角的比都
是7:2,求这个多边形的边数.
课堂检测
1.判断.
(1)当多边形边数增加时,它的内角和也随着增加.( )
(2)当多边形边数增加时,它的外角和也随着增加.( )
(3)三角形的外角和与八边形的外角和相等. ( )
2.一个正多边形的内角和为720°,则这个正多边形的 每一个内角等于______.
3.如图所示,小华从点A出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是________米.
4.一个多边形的内角和不可能是( )
A.1800° B.540 ° C.720 ° D.810 °
5.一个多边形从一个顶点可引对角线3条,这个多边形
内角和等于( )
A.360° B.540 ° C.720 ° D.900 °
6. 一个多边形的内角和为1800°,截去一个角后,求得到的多边形的内角和.
归纳总结
多边形的内角和
内角和计算公式
(n-2) × 180 °(n ≥3的整数)
外角和
多边形的外角和等于360°
特别注意:与边数无关.
正多
边形
内角= ,外角=
11.3.2 多边形的内角和
第十一章 三角形
11.3 多边形及其内角和
璧山区正则中学 薛霁
问题2 你知道长方形和正方形的内角和是多少 度?
问题1 三角形内角和是多少度?
问题3 猜想任意四边形的内角和是多少度?
探究一 多边形的内角和
猜想与证明
A
B
C
D
将四边形转化为两个三角形
猜想:四边形ABCD的内角和是360°
问题4 你能用以前学过的知识说明一下你的结论吗?
A
C
D
E
B
A
B
C
D
E
F
问题5 你能仿照求四边形内角和的方法,求五边形和六边形内角和吗
内角和为180° ×3 = 540°.
内角和为180° ×4 = 720°.
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一顶点引出的对角线条数
图形
边数
······
0
n -3
1
2
3
1
2
3
4
n -2
( n -2 )·180
1×180 =180
2×180 =360
3×180 =540
4×180 =720
······
······
······
······
由特殊到一般
多边形
三角形
转化思想
总结归纳
多边形的内角和公式
n边形内角和等于(n-2)×180 °.
例1:如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.
A
B
C
D
如果一个四边形的一组对角互补,那么另一组对角互补.
【变式题】如图,在四边形ABCD中,∠A与∠C互补,BE平分∠ABC,DF平分∠ADC,若BE∥DF,求证:△DCF为直角三角形.
例2 一个多边形的内角和比四边形的内角和多720°,并且这个多边形的各内角都相等,这个多边形的每个内角是多少度?
探究三 多边形的外角和
如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.
问题1:任意一个外角和它相邻的内角有什么关系?
问题2:五个外角加上它们分别相邻的五个内角和是多少?
问题3:这五个平角和与五边形的内角和、外角和有什么关系?
E
B
C
D
1
2
3
4
5
A
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
n边形的外角和等于360°.
-(n-2) × 180°
=360 °
=n个平角-n边形内角和
= n×180 °
An
A2
A3
A4
1
2
3
4
n
A1
思考:n边形的外角和又是多少呢?
与边数无关
问题4:回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?为什么?
每个内角的度数是
每个外角的度数是
课堂练习:书24页练习题1、2、3
例3 已知一个多边形,它的内角和等于外角和的
2倍,求这个多边形的边数.
例4 已知一个多边形的每个内角与外角的比都
是7:2,求这个多边形的边数.
课堂检测
1.判断.
(1)当多边形边数增加时,它的内角和也随着增加.( )
(2)当多边形边数增加时,它的外角和也随着增加.( )
(3)三角形的外角和与八边形的外角和相等. ( )
2.一个正多边形的内角和为720°,则这个正多边形的 每一个内角等于______.
3.如图所示,小华从点A出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是________米.
4.一个多边形的内角和不可能是( )
A.1800° B.540 ° C.720 ° D.810 °
5.一个多边形从一个顶点可引对角线3条,这个多边形
内角和等于( )
A.360° B.540 ° C.720 ° D.900 °
6. 一个多边形的内角和为1800°,截去一个角后,求得到的多边形的内角和.
归纳总结
多边形的内角和
内角和计算公式
(n-2) × 180 °(n ≥3的整数)
外角和
多边形的外角和等于360°
特别注意:与边数无关.
正多
边形
内角= ,外角=
