解三角形应用举例[上学期](正余弦定理在测量中的应用)
文档属性
| 名称 | 解三角形应用举例[上学期](正余弦定理在测量中的应用) |  | |
| 格式 | rar | ||
| 文件大小 | 704.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-23 07:22:00 | ||
图片预览




文档简介
课件13张PPT。复习1、请回答下列问题:复习2. 下列解△ABC问题, 分别属于那种类型?根据哪个定理可以先求什么元素? 第4小题A变更为A=150o呢?_____________________余弦定理先求出A,或先求出B正弦定理先求出B(60o或120o)余弦定理先求出a无解正弦定理先求出b1.2 应用举例 正弦定理和余弦定理在实际测量中有许多应用,可以解决实际中的距离、高度、角度等解三角形的应用----
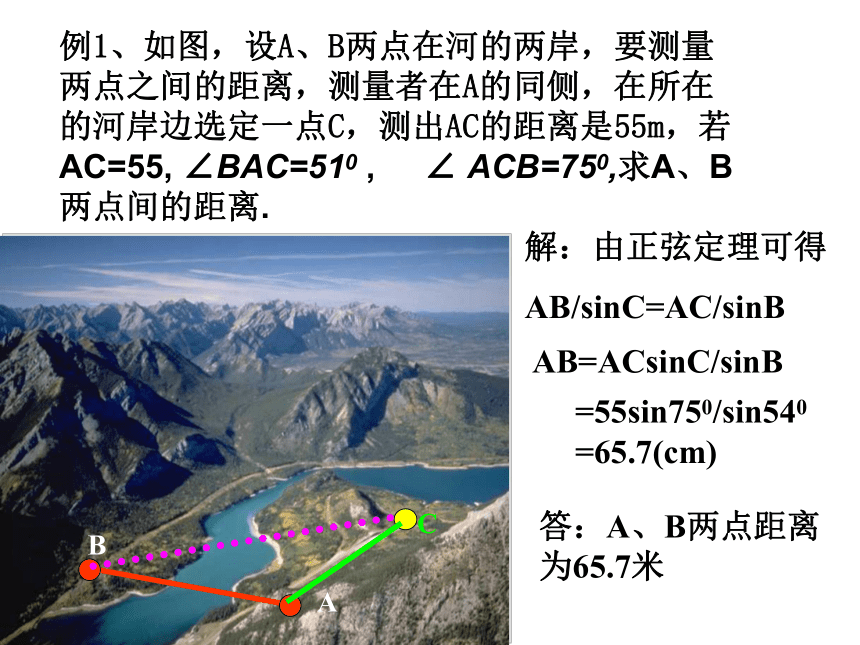
实地测量举例想一想: 如何测定河两岸两点A、B间的距离?ABABC例1、如图,设A、B两点在河的两岸,要测量两点之间的距离,测量者在A的同侧,在所在的河岸边选定一点C,测出AC的距离是55m,若AC=55, ∠BAC=510 ,α ∠ ACB=750,求A、B两点间的距离.解:由正弦定理可得
AB/sinC=AC/sinB
AB=ACsinC/sinB=55sin750/sin540=65.7(cm)答:A、B两点距离为65.7米解三角形的应用---
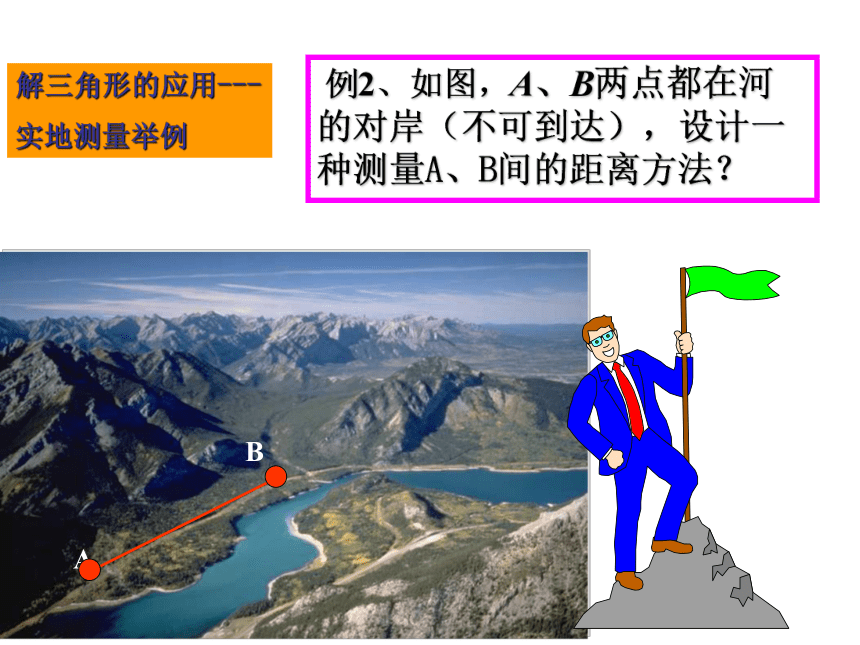
实地测量举例 例2、如图,A、B两点都在河的对岸(不可到达),设计一种测量A、B间的距离方法?AB如图在河这边取一点,构造三角形ABC,能否求出AB?为什么?
CD1、分析:理解题意,画出示意图 2、建模:把已知量与求解量集中在一个三角形中3、求解:运用正弦定理和余弦定理,有顺序地解这些三角形,求得数学模型的解。4、检验:检验所求的解是否符合实际意义,从而得出实际问题的解。 实际问题→数学问题(三角形)
→数学问题的解(解三角形)→实际问题的解解三角形应用题的一般步骤是: 在例题中我们根据测量需要适当确定的线段叫做基线.练习1、自动卸货汽车的车箱采用液压机构.设计时需要计算油泵顶杆BC的长度(如图所示).已知车箱最大仰角为60?油泵顶点B与车箱支点A之间的距离为1.95m,AB与水平线之间的夹角为6?20?,AC为1.40m,计算BC的长.解:由余弦定理,得
BC2==3.571 ∴BC≈1.89(m). 答:顶杆BC约长1.89m.AB2+AC2-2AB·ACcosA1、解决应用题的思想方法是什么?2、解决应用题的步骤是什么?实际问题数学问题(画出图形)解三角形问题数学结论分析转化检验小结:把实际问题转化为数学问题,即数学建模思想。
实地测量举例想一想: 如何测定河两岸两点A、B间的距离?ABABC例1、如图,设A、B两点在河的两岸,要测量两点之间的距离,测量者在A的同侧,在所在的河岸边选定一点C,测出AC的距离是55m,若AC=55, ∠BAC=510 ,α ∠ ACB=750,求A、B两点间的距离.解:由正弦定理可得
AB/sinC=AC/sinB
AB=ACsinC/sinB=55sin750/sin540=65.7(cm)答:A、B两点距离为65.7米解三角形的应用---
实地测量举例 例2、如图,A、B两点都在河的对岸(不可到达),设计一种测量A、B间的距离方法?AB如图在河这边取一点,构造三角形ABC,能否求出AB?为什么?
CD1、分析:理解题意,画出示意图 2、建模:把已知量与求解量集中在一个三角形中3、求解:运用正弦定理和余弦定理,有顺序地解这些三角形,求得数学模型的解。4、检验:检验所求的解是否符合实际意义,从而得出实际问题的解。 实际问题→数学问题(三角形)
→数学问题的解(解三角形)→实际问题的解解三角形应用题的一般步骤是: 在例题中我们根据测量需要适当确定的线段叫做基线.练习1、自动卸货汽车的车箱采用液压机构.设计时需要计算油泵顶杆BC的长度(如图所示).已知车箱最大仰角为60?油泵顶点B与车箱支点A之间的距离为1.95m,AB与水平线之间的夹角为6?20?,AC为1.40m,计算BC的长.解:由余弦定理,得
BC2==3.571 ∴BC≈1.89(m). 答:顶杆BC约长1.89m.AB2+AC2-2AB·ACcosA1、解决应用题的思想方法是什么?2、解决应用题的步骤是什么?实际问题数学问题(画出图形)解三角形问题数学结论分析转化检验小结:把实际问题转化为数学问题,即数学建模思想。
