北师大版六年数学上册第一单元圆的周长 学案(表格式 无答案)
文档属性
| 名称 | 北师大版六年数学上册第一单元圆的周长 学案(表格式 无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 135.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-08 10:10:48 | ||
图片预览

文档简介
课题 北师大版六年数学上册第一单元圆的周长学案
知识点 一、圆的周长和直径的关系。 已知圆的直径,求圆的周长,可用公式C=πd来求;已知圆的周长,求直径,可用公式d=来求。 二、圆的周长和半径的关系。 因为直径是半径的2倍,即d=2r,所以已知圆的半径,求圆的周长可用公式C=2πr来计算。
重点 探索、发现圆的周长和直径的关系。
突破思路 运用滚动、绕线等方法,让学生动手测量、计算,发现圆的周长和直径的关系。
难点 运用圆的周长解决一些简单的实际问题。
突破思路 根据问题的已知条件,通过分析、理解,运用圆的周长和直径的关系解决实际问题。
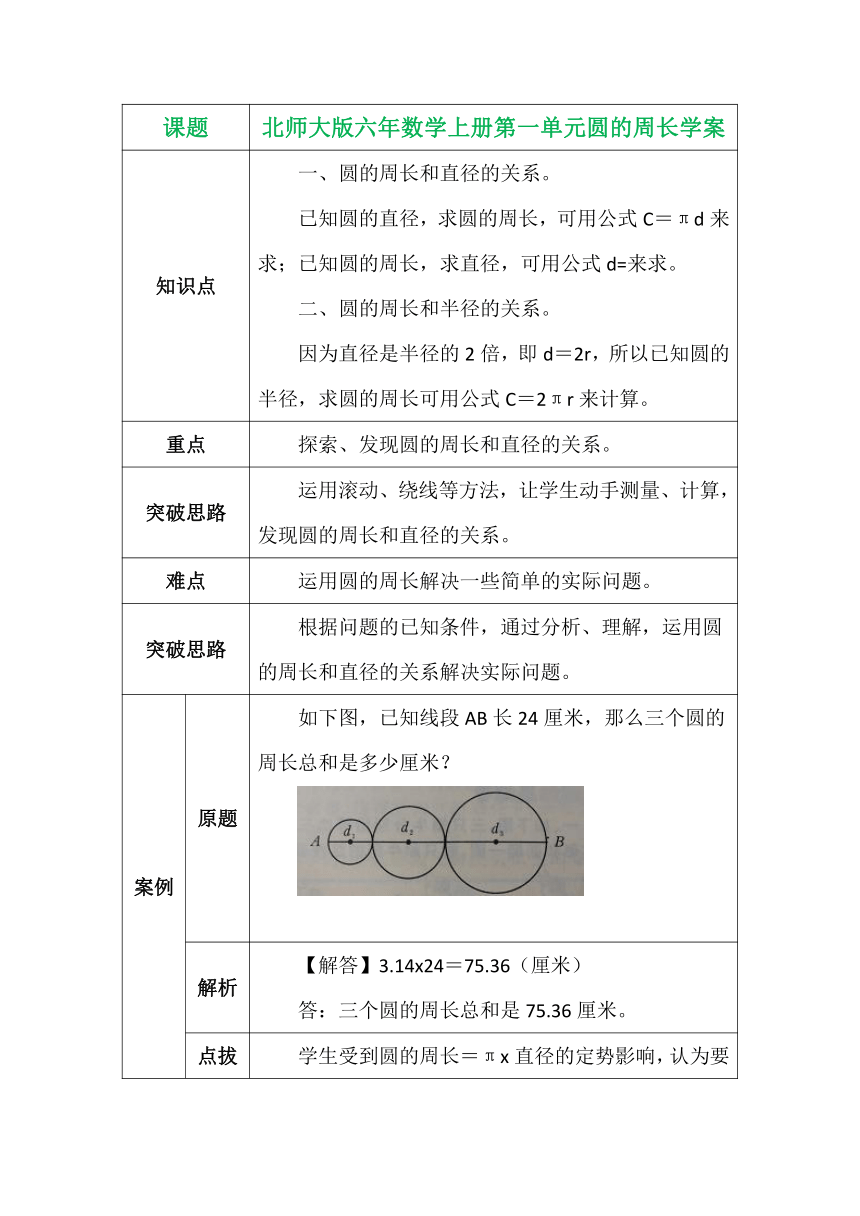
案例 原题 如下图,已知线段AB长24厘米,那么三个圆的周长总和是多少厘米?
解析 【解答】3.14x24=75.36(厘米) 答:三个圆的周长总和是75.36厘米。
点拔 学生受到圆的周长=πx直径的定势影响,认为要用公式C=πd来求出每个圆的周长后再求三个圆的周长总和,在题目没有直接给出每个圆的直径的情况下,感到无从下手。有的学生会采用估测的方法,先估计出每个圆的直径再进行计算,这种方法是错误的。
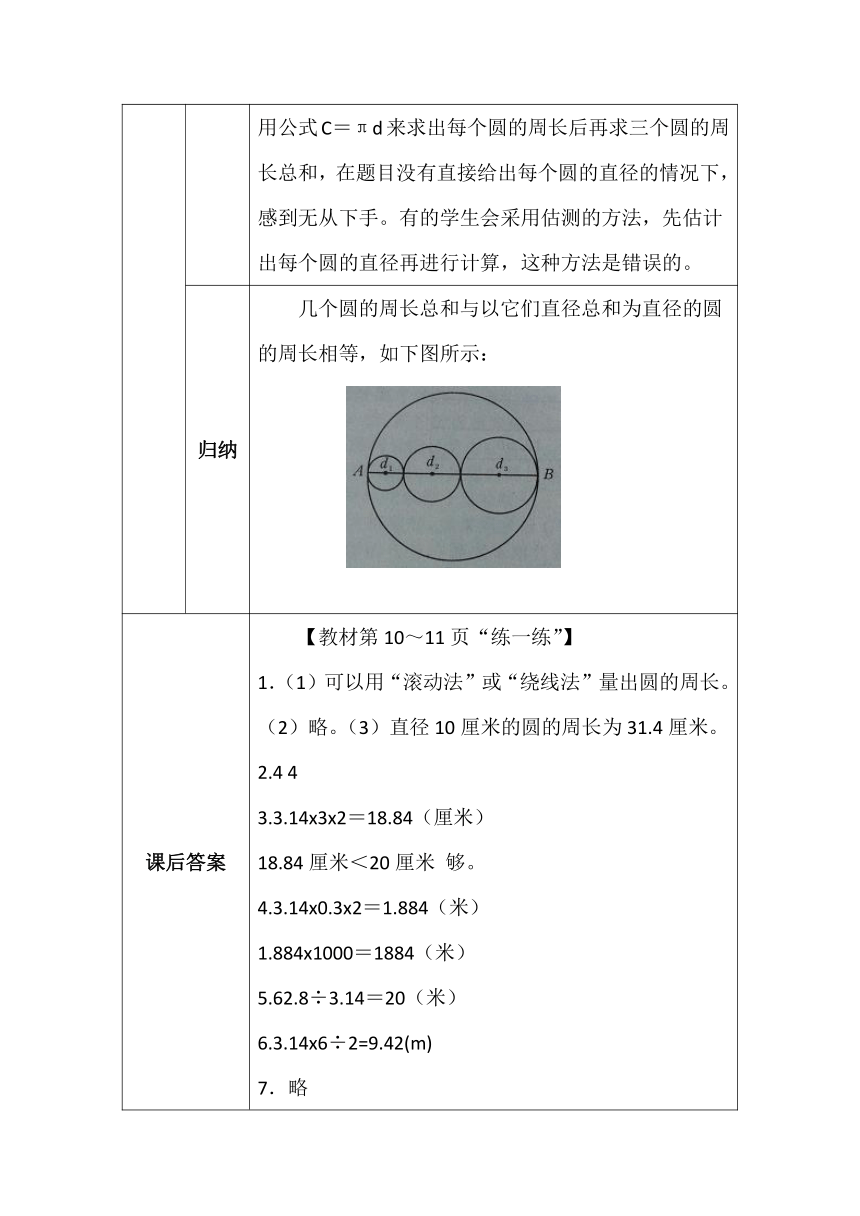
归纳 几个圆的周长总和与以它们直径总和为直径的圆的周长相等,如下图所示:
课后答案 【教材第10~11页“练一练”】 1.(1)可以用“滚动法”或“绕线法”量出圆的周长。(2)略。(3)直径10厘米的圆的周长为31.4厘米。 2.4 4 3.3.14x3x2=18.84(厘米) 18.84厘米<20厘米 够。 4.3.14x0.3x2=1.884(米) 1.884x1000=1884(米) 5.62.8÷3.14=20(米) 6.3.14x6÷2=9.42(m) 7.略 8.10x3.14=31.4(米)
作 业 (课后余下习题。)
存在问 题摘要 (1). ; (2). ; (3). 。
反思 本课的教学内容是圆的周长,这是在学习了长方形、正方形的周长以及初步认识了圆的基础上进行教学的。在本节课的教学中,我首先用不同大小的车轮滚动一圈的长短引入圆周长的概念,再引导学生通过测量圆的周长探究圆周长的计算公式。为了让学生更好地理解本节课的内容,我设计了几个不同的问题,如:“可以用哪些方法测量圆的周长”“圆的周长和什么有关”等,让学生一边思考解决问题,一边动手操作,这种把主动权充分让给学生的教学方法,大大激发了学生的学习兴趣。当学生通过自己的努力解决了问题后,一个个都露出笑容,学习的劲头更足了。
课外资料 π的其他计算方法 在1777年出版的《或然性算术实验》一书中,法国数学家蒲丰提出了用实验计算π的方法。这个实验方法的操作很简单:找一根粗细均匀,长度为d的细针,并在一张白纸上画上一组间距为l的平行线(方便起见,常取l=),然后一次又一次地将小针任意投掷在白纸上。这样反复地投多次,针与任意平行线相交的次数,就是π的近似值。在一次实验中,他共计投针2212次,其中针与平行线相交704次,这样求得圆周率的近似值为2212÷704≈3.142。实验中投的次数越多,π的值就越精确。
知识点 一、圆的周长和直径的关系。 已知圆的直径,求圆的周长,可用公式C=πd来求;已知圆的周长,求直径,可用公式d=来求。 二、圆的周长和半径的关系。 因为直径是半径的2倍,即d=2r,所以已知圆的半径,求圆的周长可用公式C=2πr来计算。
重点 探索、发现圆的周长和直径的关系。
突破思路 运用滚动、绕线等方法,让学生动手测量、计算,发现圆的周长和直径的关系。
难点 运用圆的周长解决一些简单的实际问题。
突破思路 根据问题的已知条件,通过分析、理解,运用圆的周长和直径的关系解决实际问题。
案例 原题 如下图,已知线段AB长24厘米,那么三个圆的周长总和是多少厘米?
解析 【解答】3.14x24=75.36(厘米) 答:三个圆的周长总和是75.36厘米。
点拔 学生受到圆的周长=πx直径的定势影响,认为要用公式C=πd来求出每个圆的周长后再求三个圆的周长总和,在题目没有直接给出每个圆的直径的情况下,感到无从下手。有的学生会采用估测的方法,先估计出每个圆的直径再进行计算,这种方法是错误的。
归纳 几个圆的周长总和与以它们直径总和为直径的圆的周长相等,如下图所示:
课后答案 【教材第10~11页“练一练”】 1.(1)可以用“滚动法”或“绕线法”量出圆的周长。(2)略。(3)直径10厘米的圆的周长为31.4厘米。 2.4 4 3.3.14x3x2=18.84(厘米) 18.84厘米<20厘米 够。 4.3.14x0.3x2=1.884(米) 1.884x1000=1884(米) 5.62.8÷3.14=20(米) 6.3.14x6÷2=9.42(m) 7.略 8.10x3.14=31.4(米)
作 业 (课后余下习题。)
存在问 题摘要 (1). ; (2). ; (3). 。
反思 本课的教学内容是圆的周长,这是在学习了长方形、正方形的周长以及初步认识了圆的基础上进行教学的。在本节课的教学中,我首先用不同大小的车轮滚动一圈的长短引入圆周长的概念,再引导学生通过测量圆的周长探究圆周长的计算公式。为了让学生更好地理解本节课的内容,我设计了几个不同的问题,如:“可以用哪些方法测量圆的周长”“圆的周长和什么有关”等,让学生一边思考解决问题,一边动手操作,这种把主动权充分让给学生的教学方法,大大激发了学生的学习兴趣。当学生通过自己的努力解决了问题后,一个个都露出笑容,学习的劲头更足了。
课外资料 π的其他计算方法 在1777年出版的《或然性算术实验》一书中,法国数学家蒲丰提出了用实验计算π的方法。这个实验方法的操作很简单:找一根粗细均匀,长度为d的细针,并在一张白纸上画上一组间距为l的平行线(方便起见,常取l=),然后一次又一次地将小针任意投掷在白纸上。这样反复地投多次,针与任意平行线相交的次数,就是π的近似值。在一次实验中,他共计投针2212次,其中针与平行线相交704次,这样求得圆周率的近似值为2212÷704≈3.142。实验中投的次数越多,π的值就越精确。
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
