余弦定理[下学期]
图片预览






文档简介
课件15张PPT。余弦定理欢迎各位光临指导!在直角三角形中,有对于一个直角三角形来说,它的
斜边的平方等于两直角边的平方
和。那么对于任一三角形来说,
是否也可以根据任一两边和它们
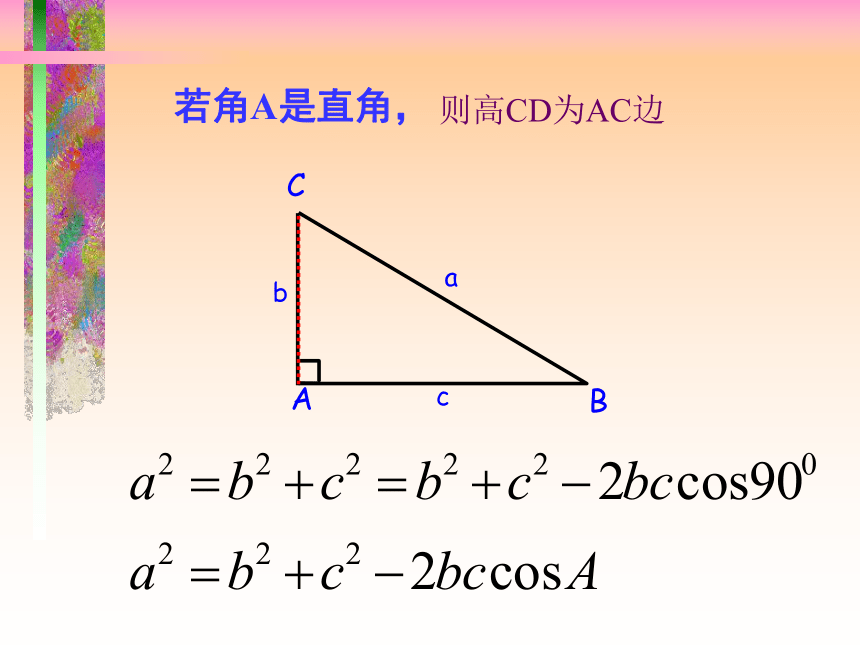
的夹角,求出夹角的对边呢?ACBcba如图,过C作CD垂直AB于D,则CABDb已知两边b ,c及夹角A,求三角形的a.ca若为钝角三角形(角A是钝角),ABCabcD则高CD在三角形的外部若角A是直角,CABbca则高CD为AC边C点的坐标为( )xyB(c,0)Cbc如图,以点A为原点,边AB所在直线为x轴建立直角坐标系a(0,0)三。向量法:
在三角形ABC中,AB=c,BC=a,CA=b.同理可证: 余弦定理:三角形任一边的平方等于其它
两边平方的和减去这两边与
它们夹角的余弦的积的两倍。由此可见,余弦定理是勾股定理的推广!例1:在三角形ABC中,已知a=7,b=10,c=6
求A、B和C。(精确到1度)例2。在三角形ABC中,已知a=2.730,b=3.696
C= ,解这个三角形(边长保留四个
有效数字,角度精确到1分)。解:由 得 c=4.297.总结:利用余弦定理,可以解决以下两类有关三角形的问题:(1)已知三边求三个角;
(2)已知两边和它们的夹角,求第三边和其它角练习 (1)已知b=8, c=3, A= 求a;
(2)已知a=20, b=29, c=21, 求B;
(3)已知a= 求b;
(4)已知a=2, 求A。在三角形ABC中:解:(1)2.在 中, 判断 的形状。解:acosA=bcosB
由余弦定理得:二.三种证明方法的比较:几何法:通过作高,把一般三角形转化为直角三
角形求证(化一般为特殊)解析法:通过建立直角坐标系,把几何问题用代数的方
法解决(几何问题代数化)
向量法:通过向量的知识来证明。回顾与小结一、余弦定理:作业:习题6、9谢谢各位老师的指导!!!
斜边的平方等于两直角边的平方
和。那么对于任一三角形来说,
是否也可以根据任一两边和它们
的夹角,求出夹角的对边呢?ACBcba如图,过C作CD垂直AB于D,则CABDb已知两边b ,c及夹角A,求三角形的a.ca若为钝角三角形(角A是钝角),ABCabcD则高CD在三角形的外部若角A是直角,CABbca则高CD为AC边C点的坐标为( )xyB(c,0)Cbc如图,以点A为原点,边AB所在直线为x轴建立直角坐标系a(0,0)三。向量法:
在三角形ABC中,AB=c,BC=a,CA=b.同理可证: 余弦定理:三角形任一边的平方等于其它
两边平方的和减去这两边与
它们夹角的余弦的积的两倍。由此可见,余弦定理是勾股定理的推广!例1:在三角形ABC中,已知a=7,b=10,c=6
求A、B和C。(精确到1度)例2。在三角形ABC中,已知a=2.730,b=3.696
C= ,解这个三角形(边长保留四个
有效数字,角度精确到1分)。解:由 得 c=4.297.总结:利用余弦定理,可以解决以下两类有关三角形的问题:(1)已知三边求三个角;
(2)已知两边和它们的夹角,求第三边和其它角练习 (1)已知b=8, c=3, A= 求a;
(2)已知a=20, b=29, c=21, 求B;
(3)已知a= 求b;
(4)已知a=2, 求A。在三角形ABC中:解:(1)2.在 中, 判断 的形状。解:acosA=bcosB
由余弦定理得:二.三种证明方法的比较:几何法:通过作高,把一般三角形转化为直角三
角形求证(化一般为特殊)解析法:通过建立直角坐标系,把几何问题用代数的方
法解决(几何问题代数化)
向量法:通过向量的知识来证明。回顾与小结一、余弦定理:作业:习题6、9谢谢各位老师的指导!!!
