余弦定理[上学期]
图片预览







文档简介
课件20张PPT。欢迎光临指导!余弦定理 淄博七中 高二数学组
杨德怀一、知识点复习:2、三角形面积公式:
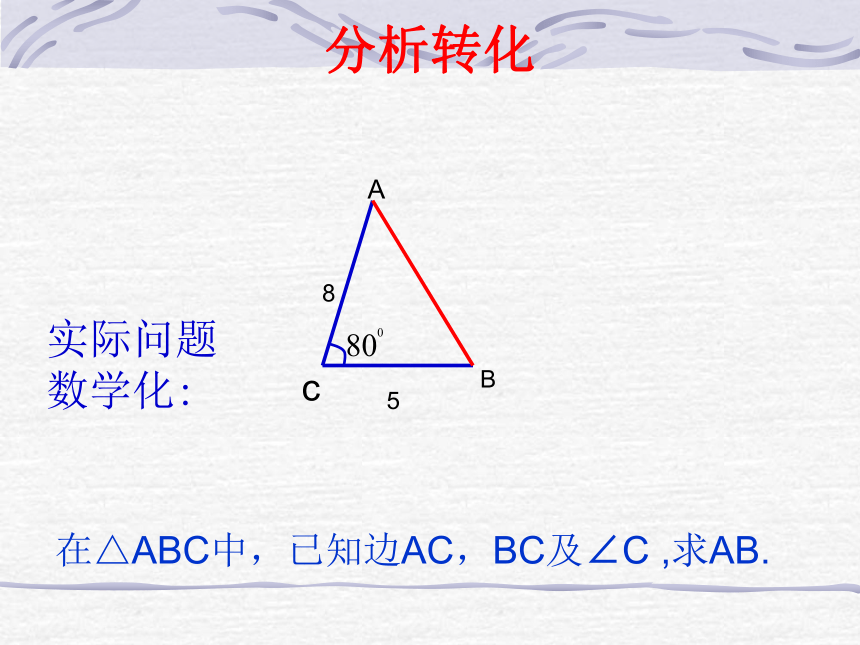
因为某种实际需要,需测量左图中A、B二点间的距离。如何测量? 实际测量中,测量人员在如图所示位置取点C,用皮尺测得AC=8米,BC=5米,∠ACB= 。由此测量人员可以得到AB的长度。
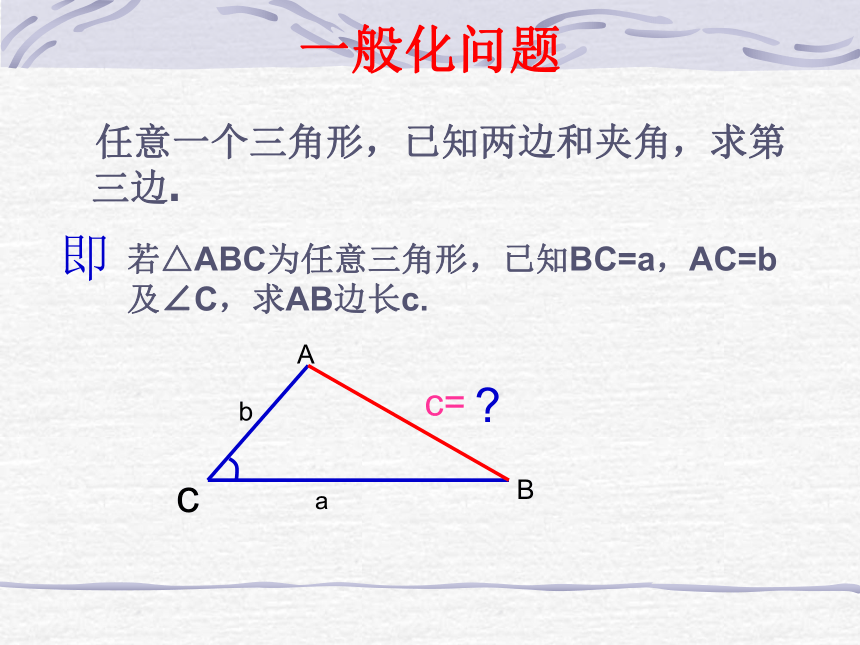
问:怎么样算AB的长度?二、课题引入:实际问题数学化: 在△ABC中,已知边AC,BC及∠C ,求AB.分析转化 任意一个三角形,已知两边和夹角,求第三边.一般化问题证明:向量法证明:以CB所在的直线为x轴,过C点垂直于CB的直线为y轴,建立如图所示的坐标系,则A、B、C三点的坐标分别为:解析法当角C为锐角时几何法
当角C为钝角时1、余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。三、新授:问题1:勾股定理与余弦定理有何关系?勾股定理是余弦定理的特例,余弦定理是勾股定理的推广.问题2:公式的结构特征怎样?(1)轮换对称,简洁优美;剖 析 定 理(2)每个等式中有同一个三角形中的四个元素,知三求一.(方程思想)
剖 析 定 理分析:(1)已知三边求三个角;问题3:余弦定理在解三角形中的作用是什么?(2)已知两边和它们的夹角,求第三边和其他两个角.剖 析 定 理四、定理应用:例2:根据所给的条件判断三角形ABC的形状。五:挑战高考:
1(2003年上海高考)在三角形ABC中,sinA: sinB:sinC=2:3:4,
则cosB=_________。2 (2001年全国)已知圆内接四边形ABCD的边长分别为
AB=2,BC=6,CD=DA=4,求四边形ABCD的面积。2.余弦定理3.余弦定理的作用(1)已知三边,求三个角;(2)已知两边和它们的夹角,求第三边和其它两角;1.证明定理的三种方法六:课堂小结谢谢大家!
杨德怀一、知识点复习:2、三角形面积公式:
因为某种实际需要,需测量左图中A、B二点间的距离。如何测量? 实际测量中,测量人员在如图所示位置取点C,用皮尺测得AC=8米,BC=5米,∠ACB= 。由此测量人员可以得到AB的长度。
问:怎么样算AB的长度?二、课题引入:实际问题数学化: 在△ABC中,已知边AC,BC及∠C ,求AB.分析转化 任意一个三角形,已知两边和夹角,求第三边.一般化问题证明:向量法证明:以CB所在的直线为x轴,过C点垂直于CB的直线为y轴,建立如图所示的坐标系,则A、B、C三点的坐标分别为:解析法当角C为锐角时几何法
当角C为钝角时1、余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。三、新授:问题1:勾股定理与余弦定理有何关系?勾股定理是余弦定理的特例,余弦定理是勾股定理的推广.问题2:公式的结构特征怎样?(1)轮换对称,简洁优美;剖 析 定 理(2)每个等式中有同一个三角形中的四个元素,知三求一.(方程思想)
剖 析 定 理分析:(1)已知三边求三个角;问题3:余弦定理在解三角形中的作用是什么?(2)已知两边和它们的夹角,求第三边和其他两个角.剖 析 定 理四、定理应用:例2:根据所给的条件判断三角形ABC的形状。五:挑战高考:
1(2003年上海高考)在三角形ABC中,sinA: sinB:sinC=2:3:4,
则cosB=_________。2 (2001年全国)已知圆内接四边形ABCD的边长分别为
AB=2,BC=6,CD=DA=4,求四边形ABCD的面积。2.余弦定理3.余弦定理的作用(1)已知三边,求三个角;(2)已知两边和它们的夹角,求第三边和其它两角;1.证明定理的三种方法六:课堂小结谢谢大家!
