5.10解斜三角形应用举例[下学期]
文档属性
| 名称 | 5.10解斜三角形应用举例[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 650.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2005-10-02 16:42:00 | ||
图片预览



文档简介
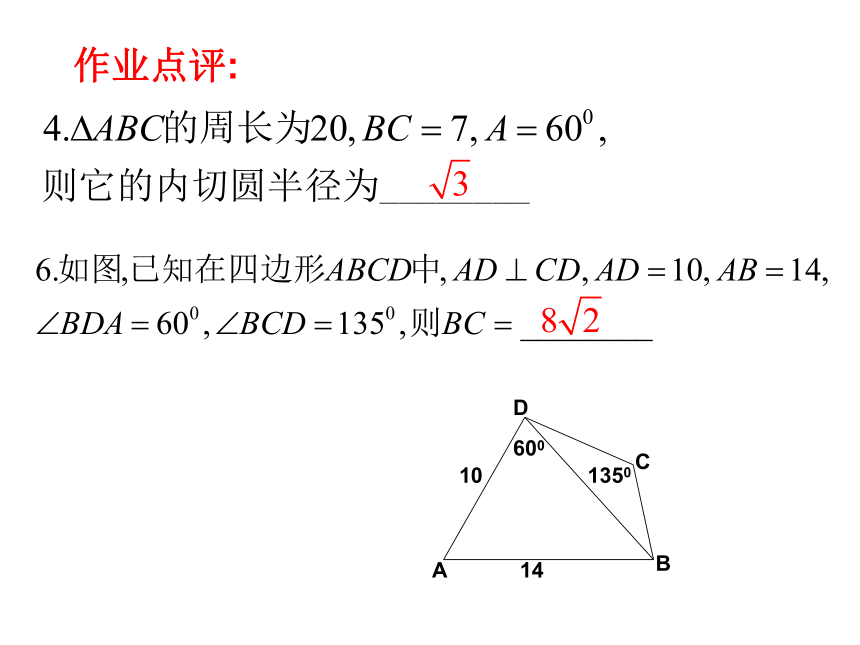
课件17张PPT。5.10解斜三角形应用举例一.正弦定理二、余弦定理 复习:作业点评:例1、自动卸货汽车的车箱采用液压机构。设计时需要计算油泵
顶杠BC的长度(如图所示)。已知车箱的最大仰角为 ,油
泵顶点B与车箱支点A之间的距离为1.95m,AB与水平线之间的
夹角为 ,AC长为1.40m,计算BC的长(保留三个有效数
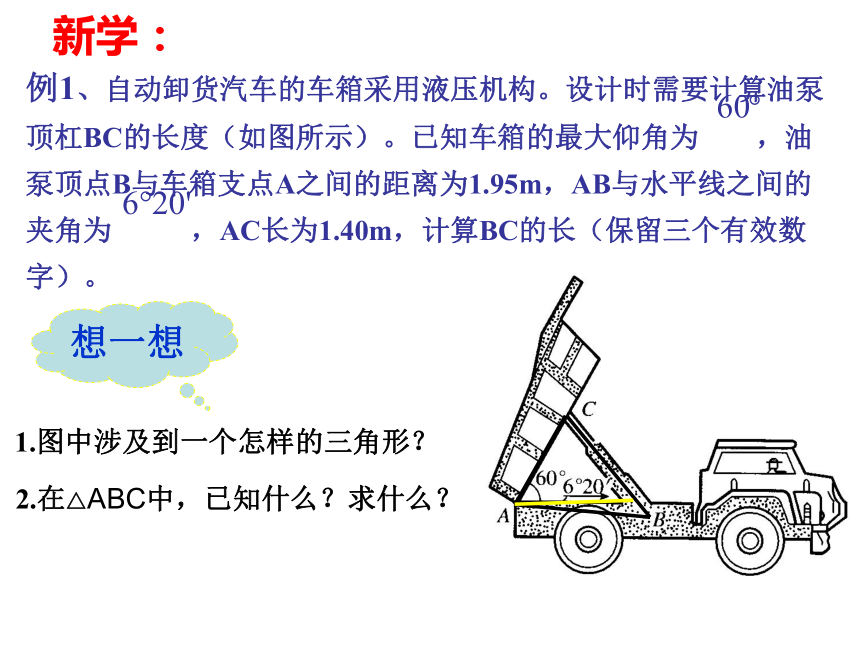
字)。想一想1.图中涉及到一个怎样的三角形?2.在△ABC中,已知什么?求什么?新学:2.在△ABC中,已知什么?求什么?1.图中涉及到一个怎样的三角形?想一想例1、自动卸货汽车的车箱采用液压机构。设计时需要计算油泵
顶杠BC的长度(如图所示)。已知车箱的最大仰角为 ,油
泵顶点B与车箱支点A之间的距离为1.95m,AB与水平线之间的
夹角为 ,AC长为1.40m,计算BC的长(保留三个有效数
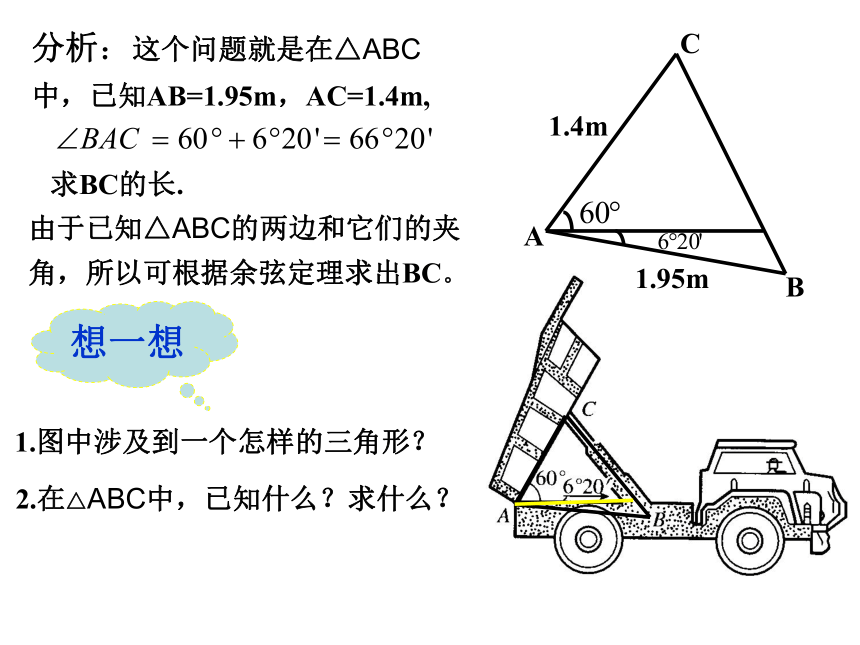
字)。1.4m1.95m分析:这个问题就是在△ABC
中,已知AB=1.95m,AC=1.4m,求BC的长.由于已知△ABC的两边和它们的夹角,所以可根据余弦定理求出BC。求BC的长.2.在△ABC中,已知什么?求什么?1.图中涉及到一个怎样的三角形?想一想1.4m分析:这个问题就是在△ABC
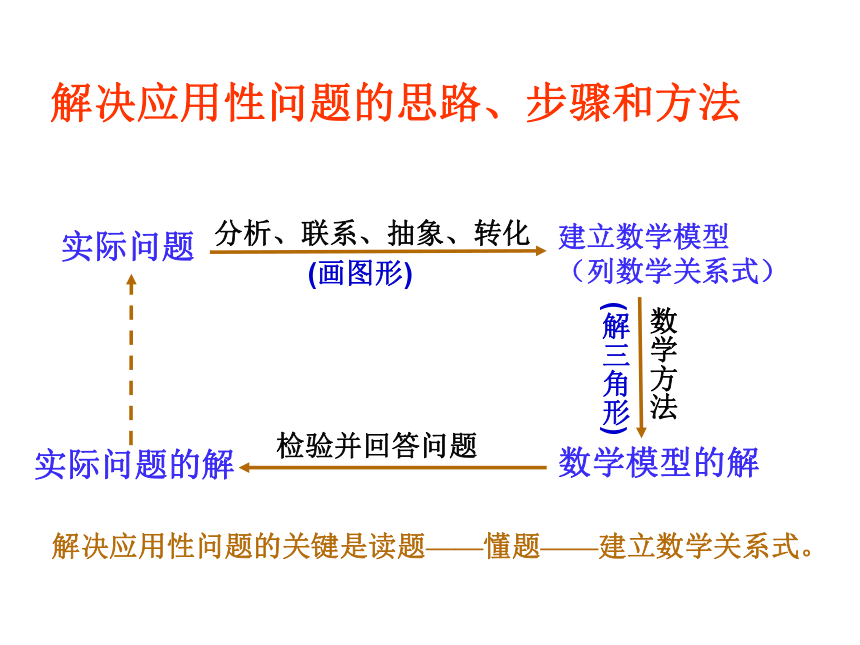
中,已知AB=1.95m,AC=1.4m,由于已知△ABC的两边和它们的夹角,所以可根据余弦定理求出BC。1.95m解:由余弦定理,得答:顶杠BC长约为1.89m.数学方法(解三角形)解决应用性问题的思路、步骤和方法实际问题 分析、联系、抽象、转化建立数学模型
(列数学关系式)数学模型的解实际问题的解解决应用性问题的关键是读题——懂题——建立数学关系式。(画图形)检验并回答问题 例2. 图中是曲柄连杆机构示意图,当曲柄CB绕C点旋转时,通
过连杆AB的传递,活塞作直线往复运动,当曲柄在CB0位置时,曲
柄和连杠成一条直线,连杠的端点A在A0处。设连杠AB长为340
mm,曲柄CB长为85mm,曲柄自CB0按顺时针方向旋转80o,求活塞
移动的距离(即连杠的端点A移动的距离A0A)(精确到1mm).分析:因为A0A=A0C-AC,又知A0C=AB+BC=340+85=425(mm),所以只要求出AC的长,问题就解决了。在△ABC中,已知两边和其中一边的对角,可由正弦定理求出AC。解:在△ABC中,由正弦定理可得因为BC 掌握利用正弦定理及余弦定理解任意三角形的方法。2、在分析问题解决问题的过程中关键要分析题意,分清已知
与所求,根据题意画出示意图,并正确运用正弦定理和余
弦定理解题。3、在解实际问题的过程中,贯穿了数学建模的思想,其流程
图可表示为:实际问题数学模型实际问题的解数学模型的解小结应用解三角形知识解实际问题的解题步骤:
(1)根据题意作出示意图;
(2)确定实际问题所涉及的三角形,并搞清该三角形的已知元和未知元;
(3)选用正、余弦定理进行求解,有时需综合运用这两个定理,并注意运算的正确性;
(4)给出答案,并检验所求的解是否符合实际意义,从而得出实际问题的解。本课小测:
(1)在某次测量中,在A处测得同一方向的B点的仰角为60o,C点的俯角为70o,则∠BAC等于( )
(A)100 (B)500 (C)1200 (D)1300
(2)若P在Q的北偏东44o50,,则Q在P的( )
(A)东偏北45o10, (B)东偏北45o50,
(C)南偏西44o50, (D)西偏南45o50,
(3)当太阳光线与地面成θ角时,长为l的木棍在地面上的影子最长为_____;
(4)在一幢高40米的楼顶测得对面一塔顶的仰角为60o,塔底的俯角为30o,则该塔高为_____米;
DC1605.1假期学习安排
1.开学后(5月8日)进行“向量”全章测验,
(题目有难度,假期要认真复习).
2.作业:创新设计107~110页(应用题两份),
129~132(全章综练一份)
顶杠BC的长度(如图所示)。已知车箱的最大仰角为 ,油
泵顶点B与车箱支点A之间的距离为1.95m,AB与水平线之间的
夹角为 ,AC长为1.40m,计算BC的长(保留三个有效数
字)。想一想1.图中涉及到一个怎样的三角形?2.在△ABC中,已知什么?求什么?新学:2.在△ABC中,已知什么?求什么?1.图中涉及到一个怎样的三角形?想一想例1、自动卸货汽车的车箱采用液压机构。设计时需要计算油泵
顶杠BC的长度(如图所示)。已知车箱的最大仰角为 ,油
泵顶点B与车箱支点A之间的距离为1.95m,AB与水平线之间的
夹角为 ,AC长为1.40m,计算BC的长(保留三个有效数
字)。1.4m1.95m分析:这个问题就是在△ABC
中,已知AB=1.95m,AC=1.4m,求BC的长.由于已知△ABC的两边和它们的夹角,所以可根据余弦定理求出BC。求BC的长.2.在△ABC中,已知什么?求什么?1.图中涉及到一个怎样的三角形?想一想1.4m分析:这个问题就是在△ABC
中,已知AB=1.95m,AC=1.4m,由于已知△ABC的两边和它们的夹角,所以可根据余弦定理求出BC。1.95m解:由余弦定理,得答:顶杠BC长约为1.89m.数学方法(解三角形)解决应用性问题的思路、步骤和方法实际问题 分析、联系、抽象、转化建立数学模型
(列数学关系式)数学模型的解实际问题的解解决应用性问题的关键是读题——懂题——建立数学关系式。(画图形)检验并回答问题 例2. 图中是曲柄连杆机构示意图,当曲柄CB绕C点旋转时,通
过连杆AB的传递,活塞作直线往复运动,当曲柄在CB0位置时,曲
柄和连杠成一条直线,连杠的端点A在A0处。设连杠AB长为340
mm,曲柄CB长为85mm,曲柄自CB0按顺时针方向旋转80o,求活塞
移动的距离(即连杠的端点A移动的距离A0A)(精确到1mm).分析:因为A0A=A0C-AC,又知A0C=AB+BC=340+85=425(mm),所以只要求出AC的长,问题就解决了。在△ABC中,已知两边和其中一边的对角,可由正弦定理求出AC。解:在△ABC中,由正弦定理可得因为BC
与所求,根据题意画出示意图,并正确运用正弦定理和余
弦定理解题。3、在解实际问题的过程中,贯穿了数学建模的思想,其流程
图可表示为:实际问题数学模型实际问题的解数学模型的解小结应用解三角形知识解实际问题的解题步骤:
(1)根据题意作出示意图;
(2)确定实际问题所涉及的三角形,并搞清该三角形的已知元和未知元;
(3)选用正、余弦定理进行求解,有时需综合运用这两个定理,并注意运算的正确性;
(4)给出答案,并检验所求的解是否符合实际意义,从而得出实际问题的解。本课小测:
(1)在某次测量中,在A处测得同一方向的B点的仰角为60o,C点的俯角为70o,则∠BAC等于( )
(A)100 (B)500 (C)1200 (D)1300
(2)若P在Q的北偏东44o50,,则Q在P的( )
(A)东偏北45o10, (B)东偏北45o50,
(C)南偏西44o50, (D)西偏南45o50,
(3)当太阳光线与地面成θ角时,长为l的木棍在地面上的影子最长为_____;
(4)在一幢高40米的楼顶测得对面一塔顶的仰角为60o,塔底的俯角为30o,则该塔高为_____米;
DC1605.1假期学习安排
1.开学后(5月8日)进行“向量”全章测验,
(题目有难度,假期要认真复习).
2.作业:创新设计107~110页(应用题两份),
129~132(全章综练一份)
