解三角形的应用举例[下学期]
图片预览






文档简介
课件28张PPT。十年树木百年树人人SZ FIRST SCHOOL教 材 分 析教学方法分析评价分析教 学 反思教材分析地位和作用
教学目标
重难点分析教材分析知识目标:进一步掌握用正余弦定理解斜三角形的方法,会利用解斜三角形的知识解决一些简单的实际问题.
能力目标:培养学生数学建模能力,探究能力和创新能力.
情感目标:培养学生数学学习兴趣、数学应用意识、交流合作精神,科学认识论思想.教材分析重点:实际问题向数学问题的转化及解斜三角形的方法.
难点:实际问题向数学问题转化思路的确定.教学方法分析教学对象分析
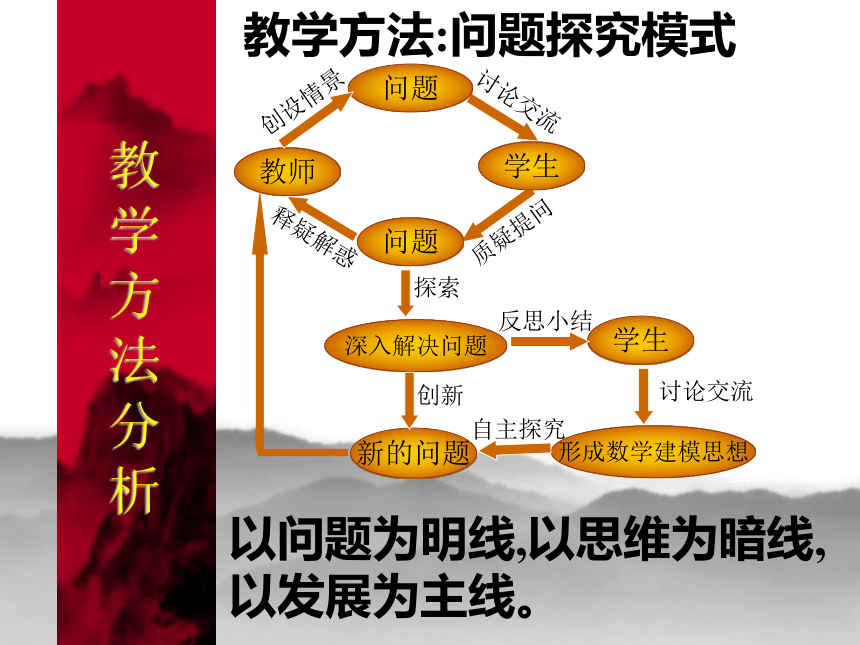
教法与学法分析教学方法分析教学方法:问题探究模式学生形成数学建模思想新的问题深入解决问题创设情景问题学生教师问题讨论交流质疑提问释疑解惑探索创新自主探究讨论交流反思小结以问题为明线,以思维为暗线,
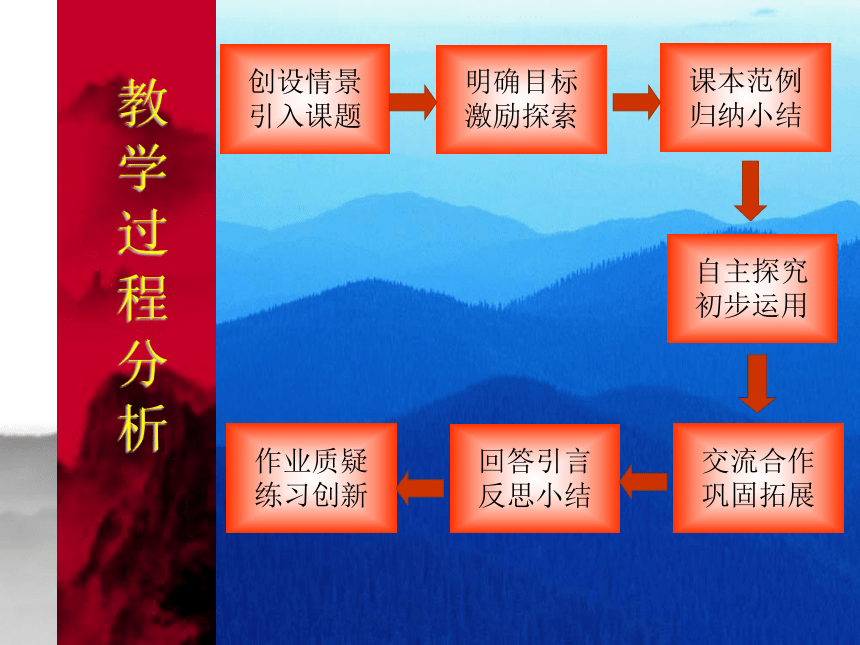
以发展为主线。教学过程分析创设情景
引入课题明确目标
激励探索课本范例
归纳小结自主探究
初步运用交流合作
巩固拓展回答引言
反思小结作业质疑
练习创新教学过程分析创设情景
引入课题明确目标
激励探索自主探究
初步运用交流合作
巩固拓展回答引言
反思小结作业质疑
练习创新课本范例
归纳小结l=?创设情景
引入课题白云湖上好风光,
游人横渡渔船忙。
湖东湖西遥相望,
谁知湖宽有多长?通过本节课我们将初步学会如何把实际问题转化成数学问题,并通过数学问题的解决最终解决实际问题。如何解决这个问题呢?明确目标
激励探索课本范例:.自动卸货汽车的车箱采用液压结构,设计时需计算油泵顶杆BC的长度。已知车箱最大仰角为600 ,油泵顶点B与车箱支点A之间的距离为1.95m,AB与水平线之间夹角落为60 20’,AC长为1.44m,计算BC的长。1.学生提问阶段:2.教师提问阶段:3.学生归纳小结:课本范例
归纳小结教学设计:1.学生提问阶段:2.教师提问阶段:3.学生归纳小结:(解释仰角俯角)课本范例::自动卸货汽车的车箱采用液压结构,设计时需计算油泵顶杆BC的长度。已知车箱最大仰角为600 ,油泵顶点B与车箱支点A之间的距离为1.95m,AB与水平线之间夹角落为60 20’,AC长为1.44m,计算BC的长。课本范例
归纳小结仰角60°教学设计:课本范例: 自动卸货汽车的车箱采用液压结构,设计时需计算油泵顶杆BC的长度。已知车箱最大仰角为600 ,油泵顶点B与车箱支点A之间的距离为1.95m,AB与水平线之间夹角落为60 20’,AC长为1.44m,计算BC的长。1.学生提问阶段:2.教师提问阶段:3.学生归纳小结:你能结合实物图画出示意图吗?你能在示意图中标出已知量未知量并转化成数学问题吗?如何解决这个数学问题?(学生讨论交流以后基本能解决这几个问题,幻灯片显示解答)ABC分析:求油泵顶杆BC的长度也就是在△ABC内,求边长BC的问题,而根据已知条件,AC=1.40m,AB=1.95 m,∠BAC=60°+6°20′=
66°20′.相当于已知△ABC的两边和它们的夹角,所以求解BC可根据余弦定理.?解:由余弦定理,得?
BC2=AB2+AC2-2AB·ACcosA
=1.952+1.402-2×1.95×1.40×cos66°20′=3.571?
∴BC≈1.89 (m)?
答:油泵顶杆BC约长1.89 m.?课本范例
归纳小结1.441..95?教学设计:课本范例: 自动卸货汽车的车箱采用液压结构,设计时需计算油泵顶杆BC的长度。已知车箱最大仰角为600 ,油泵顶点B与车箱支点A之间的距离为1.95m,AB与水平线之间夹角落为60 20’,AC长为1.44m,计算BC的长。1.学生提问阶段:2.教师提问阶段:3.学生归纳小结:课本范例
归纳小结教学设计:生活实例1: 一日小红在放学回家的路上发现一个气球悬在她正前方上空。小红用高为b的测角仪测得气球仰角为α,小红把测角仪向正前方移动了距离a,又测得气球仰角为β,你能帮小红计算气球的高度吗?2.学生交流讨论:3.教师提问:自主探究
初步运用教学设计:1.学生提问阶段:生活实例1:一日小红在放学回家的路上发现一个气球悬在她正前方上空。小红用高为b的测角仪测得气球仰角为α,小红把测角仪向正前方移动了距离a,又测得气球仰角为β,你能帮小红算气球高度吗?教学设计:1.学生提问阶段:2.学生交流讨论:3.教师提问:自主探究
初步运用(解释测角仪)教学设计:生活实例1:一日小红在放学回家的路上发现一个气球悬在她正前方上空。小红用高为b的测角仪测得气球仰角为α,小红把测角仪向正前方移动了距离a,又测得气球仰角为β,你能帮小红算气球高度吗?教学设计:2. 学生交流讨论:学生交流讨论学生
讲解学生修正补充给出解答自主探究
初步运用解:在△OAB中,AB=a , ∠OAB= α ,∠AOB= β - α ,根据正弦 定理 OB= 在Rt△OBC
中,h=OC=OBsinβ=
=
∴OD=OC+b= +b,?
答:气球的高度是
+b.答题板asinαsin(β-α)
asinα sinβsin(β-α)
ACOBDabαβh=?生活实例1:一日小红在放学回家的路上发现一个气球悬在她正前方上空。小红用高为b的测角仪测得气球仰角为α,小红把测角仪向正前方移动了距离a,又测得气球仰角为β,你能帮小红算气球高度吗?1.学生提问阶段:2.学生交流讨论:3.教师提问:自主探究
初步运用?教学设计:生活实例2:2005年9月18日广东海关某哨所发现在哨所北偏东45O方向距离为√3-1海里处有一艘走私船,在哨所北偏西75O方向距离2海里处的缉私船奉命以10 √3海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度向北偏东30O方向逃窜,缉私船沿什么方向能最快追上走私船?交流合作
巩固拓展生活实例2变式:一海岛O上有一座海拔1000m高的山,山顶上的一个观测站A上午11时测得一轮船在岛北偏东60O的C处,俯角为30O,11时10分又测得该船在岛北偏西60O的B处,俯角为60O,求该船速度,若此船不改变航速继续前进,它何时到该岛的正西方向?交流合作
巩固拓展白云湖上好风光,游人横渡渔船忙.
湖东湖西遥相望,谁知湖宽有多长回答引言
反思小结l=?βαm引言类似于生活实例1,由学生讨论后给出解答:先用测角仪测出湖对岸某参照物与湖岸线的夹角为α,沿湖岸线前进m米再测得该参照物与湖岸线夹角为β。
则
∴ l =
(亦可解斜三角形)
再次小结利用解斜三角形知识解决实际问题的一般思路。回答引言
反思小结原来如此简单!白云湖上好风光,游人横渡渔船忙.
湖东湖西遥相望,谁知湖宽有多长m作 业
1、课本习题5.10第2题和第3题。
2、运用今天所学知识测量并计算教学楼前旗杆儿的高度。
3、请在日常生活中找出两个运用了解斜三角形知识的生活实例。作业质疑
练习创新评价分析一个模式:问题探究模式
两个转变:
1.学生学习方式从接受式向活动式转变,从模仿式向探究式转变.
2.教师从课堂单一的数学知识传授者向数学学习活动的组织者,引导者与合作者转变。三条线:以问题为明线,以思维为暗线,以发展为主线.教学反思新的课程理念倡导自主、合作、探究的学习方式。为此这一节我采用了问题引导,学生讨论交流的教学方法;把问题作为教学的出发点,把学生的认识活动放在第一位,围绕问题的解决创造一个活跃愉快的课堂环境,在问题的解决过程中轻松完成数学思维过程,从而完成教学任务。在教学活动中,我设计了一些生活化趣味化的开放性例题,吸引学生自己动手、动口、动脑,鼓励学生质疑、交流、合作,而老师的作用是组织、引导、解惑。如果说课堂是一个舞台的话,那么学生就是这个舞台上的演员,而老师就是导演,引导演员发现自己的潜力,展示自己的才华!我真诚的希望通过这次的交流探讨与学习,在今后的教学中我们能真正变老师为导师,变课堂为奏响智慧之音符的乐堂!随州市第一中学
说课人: 王文莹湖北省随州市第一中学谢谢指导!湖北省随州市一中
教学目标
重难点分析教材分析知识目标:进一步掌握用正余弦定理解斜三角形的方法,会利用解斜三角形的知识解决一些简单的实际问题.
能力目标:培养学生数学建模能力,探究能力和创新能力.
情感目标:培养学生数学学习兴趣、数学应用意识、交流合作精神,科学认识论思想.教材分析重点:实际问题向数学问题的转化及解斜三角形的方法.
难点:实际问题向数学问题转化思路的确定.教学方法分析教学对象分析
教法与学法分析教学方法分析教学方法:问题探究模式学生形成数学建模思想新的问题深入解决问题创设情景问题学生教师问题讨论交流质疑提问释疑解惑探索创新自主探究讨论交流反思小结以问题为明线,以思维为暗线,
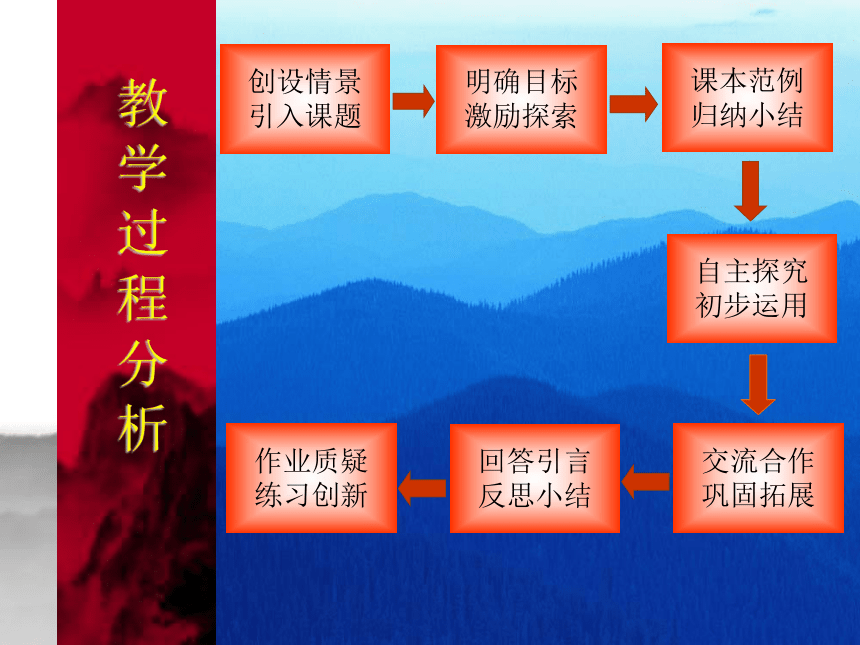
以发展为主线。教学过程分析创设情景
引入课题明确目标
激励探索课本范例
归纳小结自主探究
初步运用交流合作
巩固拓展回答引言
反思小结作业质疑
练习创新教学过程分析创设情景
引入课题明确目标
激励探索自主探究
初步运用交流合作
巩固拓展回答引言
反思小结作业质疑
练习创新课本范例
归纳小结l=?创设情景
引入课题白云湖上好风光,
游人横渡渔船忙。
湖东湖西遥相望,
谁知湖宽有多长?通过本节课我们将初步学会如何把实际问题转化成数学问题,并通过数学问题的解决最终解决实际问题。如何解决这个问题呢?明确目标
激励探索课本范例:.自动卸货汽车的车箱采用液压结构,设计时需计算油泵顶杆BC的长度。已知车箱最大仰角为600 ,油泵顶点B与车箱支点A之间的距离为1.95m,AB与水平线之间夹角落为60 20’,AC长为1.44m,计算BC的长。1.学生提问阶段:2.教师提问阶段:3.学生归纳小结:课本范例
归纳小结教学设计:1.学生提问阶段:2.教师提问阶段:3.学生归纳小结:(解释仰角俯角)课本范例::自动卸货汽车的车箱采用液压结构,设计时需计算油泵顶杆BC的长度。已知车箱最大仰角为600 ,油泵顶点B与车箱支点A之间的距离为1.95m,AB与水平线之间夹角落为60 20’,AC长为1.44m,计算BC的长。课本范例
归纳小结仰角60°教学设计:课本范例: 自动卸货汽车的车箱采用液压结构,设计时需计算油泵顶杆BC的长度。已知车箱最大仰角为600 ,油泵顶点B与车箱支点A之间的距离为1.95m,AB与水平线之间夹角落为60 20’,AC长为1.44m,计算BC的长。1.学生提问阶段:2.教师提问阶段:3.学生归纳小结:你能结合实物图画出示意图吗?你能在示意图中标出已知量未知量并转化成数学问题吗?如何解决这个数学问题?(学生讨论交流以后基本能解决这几个问题,幻灯片显示解答)ABC分析:求油泵顶杆BC的长度也就是在△ABC内,求边长BC的问题,而根据已知条件,AC=1.40m,AB=1.95 m,∠BAC=60°+6°20′=
66°20′.相当于已知△ABC的两边和它们的夹角,所以求解BC可根据余弦定理.?解:由余弦定理,得?
BC2=AB2+AC2-2AB·ACcosA
=1.952+1.402-2×1.95×1.40×cos66°20′=3.571?
∴BC≈1.89 (m)?
答:油泵顶杆BC约长1.89 m.?课本范例
归纳小结1.441..95?教学设计:课本范例: 自动卸货汽车的车箱采用液压结构,设计时需计算油泵顶杆BC的长度。已知车箱最大仰角为600 ,油泵顶点B与车箱支点A之间的距离为1.95m,AB与水平线之间夹角落为60 20’,AC长为1.44m,计算BC的长。1.学生提问阶段:2.教师提问阶段:3.学生归纳小结:课本范例
归纳小结教学设计:生活实例1: 一日小红在放学回家的路上发现一个气球悬在她正前方上空。小红用高为b的测角仪测得气球仰角为α,小红把测角仪向正前方移动了距离a,又测得气球仰角为β,你能帮小红计算气球的高度吗?2.学生交流讨论:3.教师提问:自主探究
初步运用教学设计:1.学生提问阶段:生活实例1:一日小红在放学回家的路上发现一个气球悬在她正前方上空。小红用高为b的测角仪测得气球仰角为α,小红把测角仪向正前方移动了距离a,又测得气球仰角为β,你能帮小红算气球高度吗?教学设计:1.学生提问阶段:2.学生交流讨论:3.教师提问:自主探究
初步运用(解释测角仪)教学设计:生活实例1:一日小红在放学回家的路上发现一个气球悬在她正前方上空。小红用高为b的测角仪测得气球仰角为α,小红把测角仪向正前方移动了距离a,又测得气球仰角为β,你能帮小红算气球高度吗?教学设计:2. 学生交流讨论:学生交流讨论学生
讲解学生修正补充给出解答自主探究
初步运用解:在△OAB中,AB=a , ∠OAB= α ,∠AOB= β - α ,根据正弦 定理 OB= 在Rt△OBC
中,h=OC=OBsinβ=
=
∴OD=OC+b= +b,?
答:气球的高度是
+b.答题板asinαsin(β-α)
asinα sinβsin(β-α)
ACOBDabαβh=?生活实例1:一日小红在放学回家的路上发现一个气球悬在她正前方上空。小红用高为b的测角仪测得气球仰角为α,小红把测角仪向正前方移动了距离a,又测得气球仰角为β,你能帮小红算气球高度吗?1.学生提问阶段:2.学生交流讨论:3.教师提问:自主探究
初步运用?教学设计:生活实例2:2005年9月18日广东海关某哨所发现在哨所北偏东45O方向距离为√3-1海里处有一艘走私船,在哨所北偏西75O方向距离2海里处的缉私船奉命以10 √3海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度向北偏东30O方向逃窜,缉私船沿什么方向能最快追上走私船?交流合作
巩固拓展生活实例2变式:一海岛O上有一座海拔1000m高的山,山顶上的一个观测站A上午11时测得一轮船在岛北偏东60O的C处,俯角为30O,11时10分又测得该船在岛北偏西60O的B处,俯角为60O,求该船速度,若此船不改变航速继续前进,它何时到该岛的正西方向?交流合作
巩固拓展白云湖上好风光,游人横渡渔船忙.
湖东湖西遥相望,谁知湖宽有多长回答引言
反思小结l=?βαm引言类似于生活实例1,由学生讨论后给出解答:先用测角仪测出湖对岸某参照物与湖岸线的夹角为α,沿湖岸线前进m米再测得该参照物与湖岸线夹角为β。
则
∴ l =
(亦可解斜三角形)
再次小结利用解斜三角形知识解决实际问题的一般思路。回答引言
反思小结原来如此简单!白云湖上好风光,游人横渡渔船忙.
湖东湖西遥相望,谁知湖宽有多长m作 业
1、课本习题5.10第2题和第3题。
2、运用今天所学知识测量并计算教学楼前旗杆儿的高度。
3、请在日常生活中找出两个运用了解斜三角形知识的生活实例。作业质疑
练习创新评价分析一个模式:问题探究模式
两个转变:
1.学生学习方式从接受式向活动式转变,从模仿式向探究式转变.
2.教师从课堂单一的数学知识传授者向数学学习活动的组织者,引导者与合作者转变。三条线:以问题为明线,以思维为暗线,以发展为主线.教学反思新的课程理念倡导自主、合作、探究的学习方式。为此这一节我采用了问题引导,学生讨论交流的教学方法;把问题作为教学的出发点,把学生的认识活动放在第一位,围绕问题的解决创造一个活跃愉快的课堂环境,在问题的解决过程中轻松完成数学思维过程,从而完成教学任务。在教学活动中,我设计了一些生活化趣味化的开放性例题,吸引学生自己动手、动口、动脑,鼓励学生质疑、交流、合作,而老师的作用是组织、引导、解惑。如果说课堂是一个舞台的话,那么学生就是这个舞台上的演员,而老师就是导演,引导演员发现自己的潜力,展示自己的才华!我真诚的希望通过这次的交流探讨与学习,在今后的教学中我们能真正变老师为导师,变课堂为奏响智慧之音符的乐堂!随州市第一中学
说课人: 王文莹湖北省随州市第一中学谢谢指导!湖北省随州市一中
