解三角形应用举例[上学期]
图片预览


文档简介
课件17张PPT。解三角形应用举例故宫角楼平阴县第一中学 赵延忠解三角形应用题中的几个角的概念
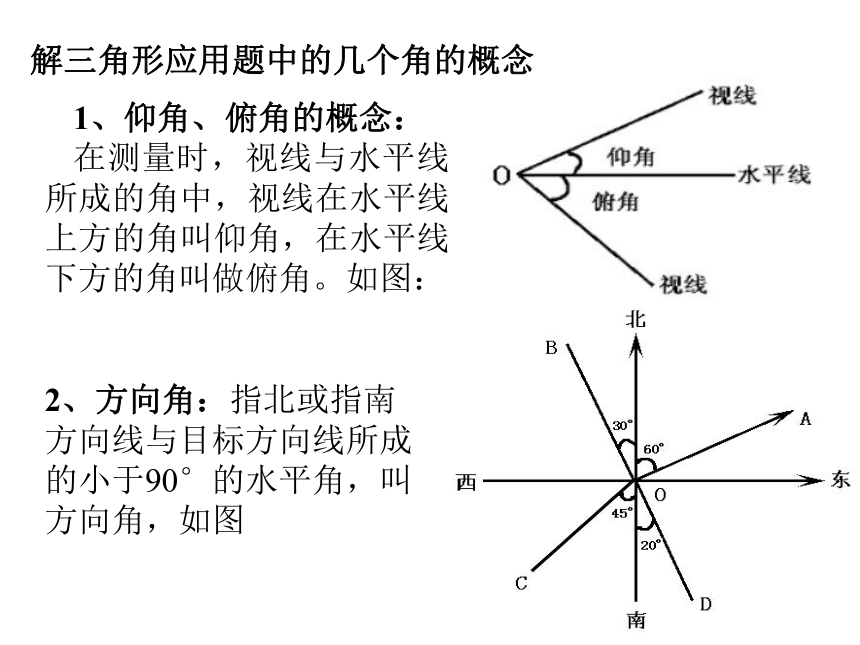
1、仰角、俯角的概念:
在测量时,视线与水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下方的角叫做俯角。如图:2、方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫方向角,如图 1、分析:理解题意,画出示意图 2、建模:把已知量与求解量集中在一个三角形中3、求解:运用正弦定理和余弦定理,有顺序地解这些三子角形,求得数学模型的解。
4、检验:检验所求的解是否符合实际意义,从而得出实际问题的解。 实际问题→数学问题(三角形)
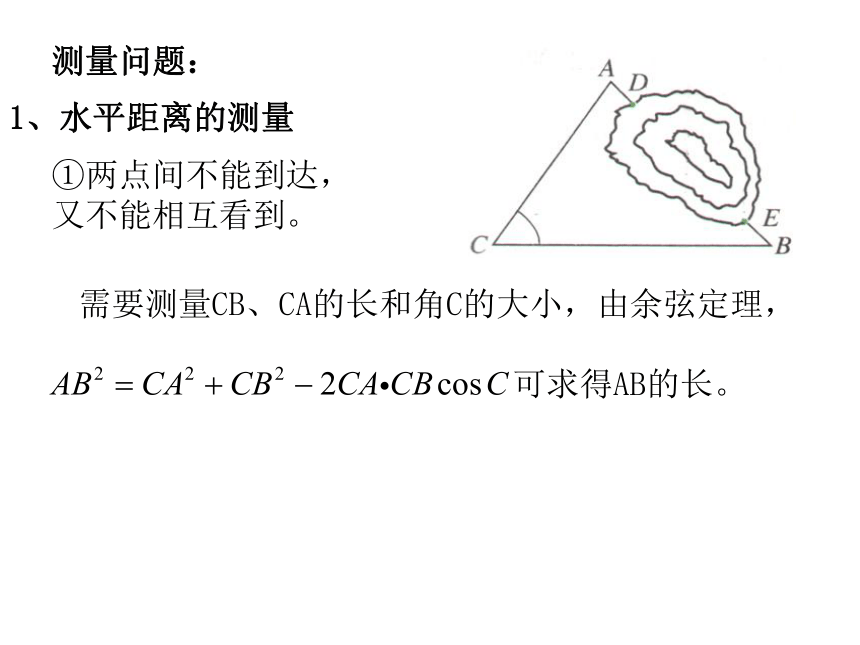
→数学问题的解(解三角形)→实际问题的解解斜三角形应用题的一般步骤是:测量问题:1、水平距离的测量①两点间不能到达,
又不能相互看到。 需要测量CB、CA的长和角C的大小,由余弦定理,
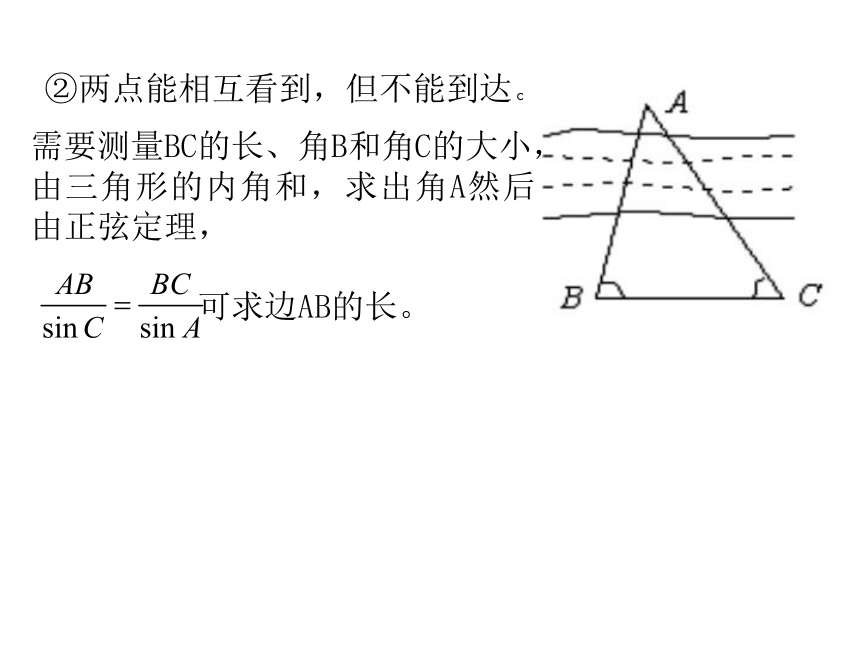
可求得AB的长。 ②两点能相互看到,但不能到达。 需要测量BC的长、角B和角C的大小,由三角形的内角和,求出角A然后由正弦定理,
可求边AB的长。
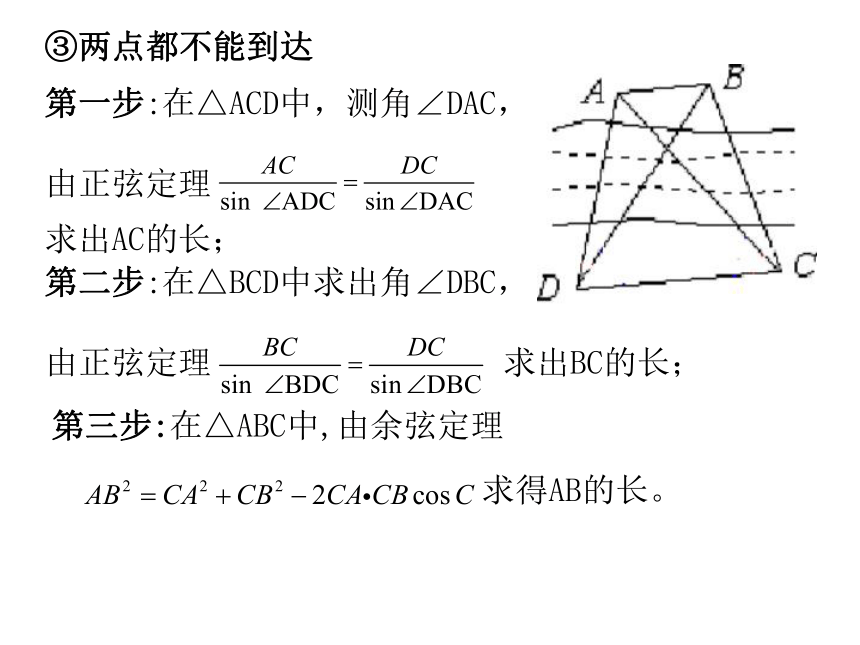
③两点都不能到达第一步:在△ACD中,测角∠DAC,
由正弦定理 求出AC的长; 第二步:在△BCD中求出角∠DBC,
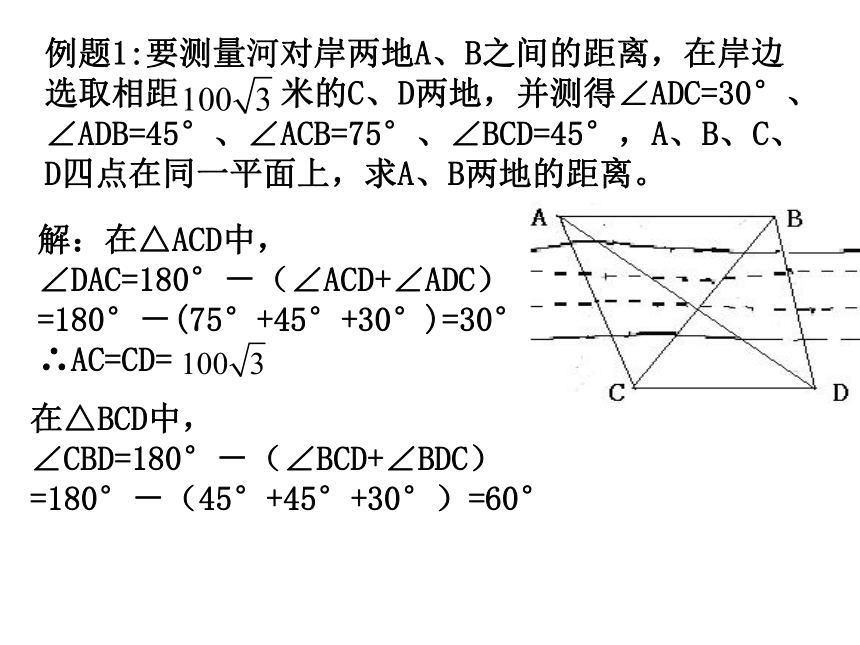
由正弦定理 求出BC的长; 第三步:在△ABC中,由余弦定理 求得AB的长。 例题1:要测量河对岸两地A、B之间的距离,在岸边选取相距 米的C、D两地,并测得∠ADC=30°、∠ADB=45°、∠ACB=75°、∠BCD=45°,A、B、C、D四点在同一平面上,求A、B两地的距离。 解:在△ACD中,
∠DAC=180°-(∠ACD+∠ADC)
=180°-(75°+45°+30°)=30°
∴AC=CD=
在△BCD中,
∠CBD=180°-(∠BCD+∠BDC)
=180°-(45°+45°+30°)=60° 由正弦定理 , 得在△ABC中由余弦定理, ∴所求A、B两地间的距离为 米。 测量垂直高度 1、底部可以到达的; 测量出角C和BC的长度,解直角三角形即可求出AB的长。 2、底部不能到达的 测量边CD,测量∠C和∠ADB,
例题2:在山顶铁塔上 处测得地面上一点 的俯角 ,在塔底 处测得点 的俯角 ,已知铁塔 部分高 米,求山高 。
解:在△ABC中,∠ABC=30°,
∠ACB =135°,
∴∠CAB =180°-(∠ACB+∠ABC)
=180°-(135°+30°)=15°
又BC=32, 由正弦定理 ,
得 在等腰Rt△ACD中,故 ∴山的高度为 米。 例题3:2004年雅典奥运会上,在垒球比赛前,某国教练为自己的球队布置了如下战术:击球手沿着本垒与游击手所在的直线夹角成 的方向把球击出,根据经验及测速仪的显示,通常的情况下,球速为游击手最快速度的4倍。请你用数学的知识来判断游击手能否接到球?并说明理由。 解:假设游击手能接到球,如图在 中,设击球点为O,落球点为B,游击手在点A,设从球击出到球被接住的时间为,球的速度为 在 中,由正弦定理,得与 相矛盾。 例题4:如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救。甲船立即前往救援,同时把消息告知在甲船的南偏西 ,相距10海里C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往处救援?
(角度精确到 )例题5:如图:点A表示某山区一移动电话信号发射塔的位置(塔高不计), 为一条东北走向的公路,技术人员为测试该发射塔信号的覆盖范围,自A点正西方向的B处骑自行车沿公路出发,约经过6分钟,发现手机开始有信号.已知AB=4,车速10,能否根据以上信息,测算出该塔信号的覆盖半径以及手机持续显示信号的时间.
例题6:某巡逻艇在A处发现北偏东45°相距9海里的C处有一艘走私船,正沿南偏东75°的方向以10海里每小时的速度向我海岸行驶,巡逻艇立即以14海里每小时的速度沿着直线方向追去,问巡逻艇应该沿什么方向去追?需要多少时间才能追赶上该走私船?
1、仰角、俯角的概念:
在测量时,视线与水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下方的角叫做俯角。如图:2、方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫方向角,如图 1、分析:理解题意,画出示意图 2、建模:把已知量与求解量集中在一个三角形中3、求解:运用正弦定理和余弦定理,有顺序地解这些三子角形,求得数学模型的解。
4、检验:检验所求的解是否符合实际意义,从而得出实际问题的解。 实际问题→数学问题(三角形)
→数学问题的解(解三角形)→实际问题的解解斜三角形应用题的一般步骤是:测量问题:1、水平距离的测量①两点间不能到达,
又不能相互看到。 需要测量CB、CA的长和角C的大小,由余弦定理,
可求得AB的长。 ②两点能相互看到,但不能到达。 需要测量BC的长、角B和角C的大小,由三角形的内角和,求出角A然后由正弦定理,
可求边AB的长。
③两点都不能到达第一步:在△ACD中,测角∠DAC,
由正弦定理 求出AC的长; 第二步:在△BCD中求出角∠DBC,
由正弦定理 求出BC的长; 第三步:在△ABC中,由余弦定理 求得AB的长。 例题1:要测量河对岸两地A、B之间的距离,在岸边选取相距 米的C、D两地,并测得∠ADC=30°、∠ADB=45°、∠ACB=75°、∠BCD=45°,A、B、C、D四点在同一平面上,求A、B两地的距离。 解:在△ACD中,
∠DAC=180°-(∠ACD+∠ADC)
=180°-(75°+45°+30°)=30°
∴AC=CD=
在△BCD中,
∠CBD=180°-(∠BCD+∠BDC)
=180°-(45°+45°+30°)=60° 由正弦定理 , 得在△ABC中由余弦定理, ∴所求A、B两地间的距离为 米。 测量垂直高度 1、底部可以到达的; 测量出角C和BC的长度,解直角三角形即可求出AB的长。 2、底部不能到达的 测量边CD,测量∠C和∠ADB,
例题2:在山顶铁塔上 处测得地面上一点 的俯角 ,在塔底 处测得点 的俯角 ,已知铁塔 部分高 米,求山高 。
解:在△ABC中,∠ABC=30°,
∠ACB =135°,
∴∠CAB =180°-(∠ACB+∠ABC)
=180°-(135°+30°)=15°
又BC=32, 由正弦定理 ,
得 在等腰Rt△ACD中,故 ∴山的高度为 米。 例题3:2004年雅典奥运会上,在垒球比赛前,某国教练为自己的球队布置了如下战术:击球手沿着本垒与游击手所在的直线夹角成 的方向把球击出,根据经验及测速仪的显示,通常的情况下,球速为游击手最快速度的4倍。请你用数学的知识来判断游击手能否接到球?并说明理由。 解:假设游击手能接到球,如图在 中,设击球点为O,落球点为B,游击手在点A,设从球击出到球被接住的时间为,球的速度为 在 中,由正弦定理,得与 相矛盾。 例题4:如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救。甲船立即前往救援,同时把消息告知在甲船的南偏西 ,相距10海里C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往处救援?
(角度精确到 )例题5:如图:点A表示某山区一移动电话信号发射塔的位置(塔高不计), 为一条东北走向的公路,技术人员为测试该发射塔信号的覆盖范围,自A点正西方向的B处骑自行车沿公路出发,约经过6分钟,发现手机开始有信号.已知AB=4,车速10,能否根据以上信息,测算出该塔信号的覆盖半径以及手机持续显示信号的时间.
例题6:某巡逻艇在A处发现北偏东45°相距9海里的C处有一艘走私船,正沿南偏东75°的方向以10海里每小时的速度向我海岸行驶,巡逻艇立即以14海里每小时的速度沿着直线方向追去,问巡逻艇应该沿什么方向去追?需要多少时间才能追赶上该走私船?
