1.5.1有理数的乘方 课件
文档属性
| 名称 | 1.5.1有理数的乘方 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 879.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-09 00:00:00 | ||
图片预览











文档简介
课件36张PPT。1.5.1
有理数的乘方
古时候,在某个王国里有一位聪明的大臣,他发明了
国际象棋,献给了国王,国王从此迷上了下棋,为了对聪
明的大臣表示感谢,国王答应满足这个大臣的一个要求。
大臣说:“就在这个棋盘上放些米粒吧。第一格放一粒米,
第二格放两粒米,第三格放4粒米,然后是8粒米、16粒、
32粒、…一直到第64格。”“你真傻!就要这么一点米粒?”
国王哈哈大笑。大臣说:“就怕您的国库里没有这么多米!”
你认为国王的国库里有这么多米吗? 事实上,按照这个大臣的要求,放满一个棋盘上的64个格子需要1+2+22+23+……+263=264-1粒米。 264到底多大呢?
答案是:18 446 744 073 709 551 616读一读
棋盘上的学问 2.如图,一正方体的棱长为a厘米, 则它的体积 为 立方厘米。a×a×a复习回顾 1.如图,边长为a厘米的正方形的面积
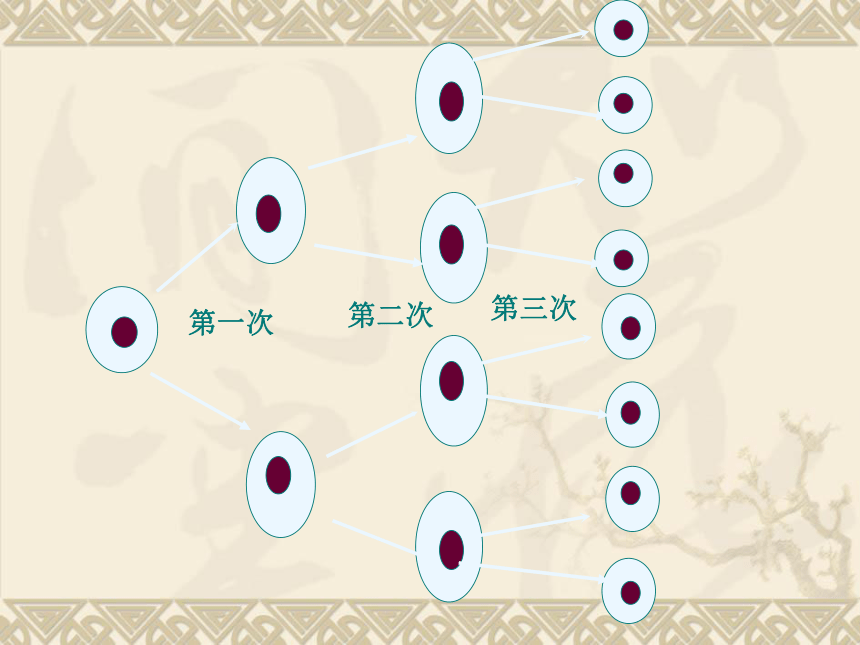
为 平方厘米。a×aaa在小学已经知道:a×a=a×a×a=读作:a的平方(或a的二次方)读作:a的立方(或a的三次方) 某种细胞 每30分钟便由一个分裂成两个。经过3小时这种细胞由1个能分裂成多少个?分裂方式如下所示:合作探究:第一次第二次第三次 这个细胞分裂一次可得多少个细胞?
那么,3小时共分裂了多少次?有多少个细胞?答:一次得:
两次 :
三次 :
四次 :2个;2×2个;2×2×2个;六次 : 2×2×2×2×2×2个.分裂两次呢?分裂三次呢?四次呢?做一做:2×2×2×2个 请比较细胞分裂四次后的个数式子:2×2×2×2和细胞分裂六次后的个数式子: 2×2×2×2×2×2.1.这两个式子有什么相同点?答:它们都是乘法;并且它们各自的因数都相同.2.同学们想一想:这样的运算能像平方、立方那样简写吗? 这样的运算我们可以像平方和立方那样简写:2×2×2×22×2×2×2×2×2记作记作一般的,任意多个相同的有理数相乘,我们通常记作:=乘方的意义 这种求n个相同因数a的积的运算叫做乘方,乘方的结果叫做幂,a叫做底数,n叫做指数,an读作a的n次幂(或a的n次方)。 (1次方可省略不写,2次方又叫平方,3次方又叫立方。)获取新知巩固新知:1、(口答)
把下列相同因数的乘积
写成幂的形式,并说出底数和指数:(1) (-6)×(-6) ×(-6)底数是 –6,指数是 3(2)底数是指数是 4温馨提示:幂的底数是分数或负数时,底数应该添上括号!填一填777底数指数-310-3-3102、把 写成几个相同因数相乘的形式3、把(-2)× (-2)× (-2)×···×(-2)10个(-2)写成幂的形式。在不会引起误解的情况下,乘号也可以用“·”表示。例如:(-3)×(-3)×(-3) ×(-3)可写成(-3)·(-3)·(-3)·(-3)7底指12的10次方 底指-3的16次方17对错错错试试你的火眼金睛思考:说说下列各数的意义,它们一样吗?
表示3个2相乘表示2个3相乘试试你的火眼金睛思考:请指出下列幂的底数与指数并说说下列各数的意义,它们一样吗?试试你的火眼金睛思考:说说下列各数的意义,它们一样吗?
要注意哟!对于分数的乘方,负数的乘方,书写时一定要注意小括号,这也是辩认底数的方法. 写出算式=3×3×3×3=81=(-3)×(-3)×(-3)×(-3)=+81写出算式注意符号解题步骤与思路★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★错误的原因是仅将分子乘方,不将分母乘方。注意,应将分数全体乘方。同号两数相乘符号为正=-(4×4)
=-16-号保留不变计算计算(观察各题结果,你能发现乘方运算的符号有什么规律?)
(1)32 24 16
(2)51 23 19
(3)(-9)2 (-2)6 (-3)4
(4)(-2)5 (-3)3 (-1)3
(5)02 03 04 09
有理数乘方的规律
1、正数的任何次幂都是正数
2、负数的偶次幂是正数,负数的奇次幂是负数
3 、零的任何正整数次幂都是零一 不做运算,判断下列各运算结果的符号
(-3)13 (-2)24 (-1.7)2003
-(-2)23 02004 (-3.9)12注意:“一看底数,二看指数”
当底数是正数时,结果为正;当底数是0时,结果是0;
当底数是负数时,再看指数,若指数为偶数,结果为正,
若指数是奇数,结果为负(1) (2)
(3) (4)
(5) (6)
=1=1=-1=1=1=-1口答(1) 1的任何次幂都为 1。(2) -1的奇次幂是-1 ,
-1的偶次幂是1。规律:1001000;100-100010000抢答练习:计算10000(1)正数的任次幂为正;负数的偶次 幂为正
奇次幂为负 0.01;-0.001返回下一张上一张退出抢答练习:计算0.00010.01;0.001;0.0001规律:
(1)正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数。0的任何次幂都是0.
(2)底数绝对值为10的幂的特点:1后面0的个数与指数相同。
(3)底数绝对值为0.1的幂的特点:1前面0的个数与指数相同(包括小数点前的1个零。(1) (2) (3) 1)、计 算达标训练 2) 在94中,底数是 ,指数是 ,读作 ,或读作 ;
3) 在(-2)3中,底数是 ,指数是 ,读作 ,或读作 ;
4) 在 中,底数是 ,指数是 ,读作 ;
5) 在 5 中,底数是 ,指数是 ;
6) 02 = ,03 = , 04 = ;
7)23 = ,24 = , 25 = ;
8)(-3)2 = ,(-3)3 = ,(-3)4 = , (-3)5 = ;猜一猜这节课你学会了一种什么运算?你有何体会?反思“乘方”精神:虽然是简简单单的重复,但结果却是惊人的。做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。(2)负数的乘方,在书写时一定要把整个负数(连同符号),用小括号括起来.分数的乘方,在书写的时一定要把整个分数用 小括号括起来.(1)正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数.同学们
再
见!
有理数的乘方
古时候,在某个王国里有一位聪明的大臣,他发明了
国际象棋,献给了国王,国王从此迷上了下棋,为了对聪
明的大臣表示感谢,国王答应满足这个大臣的一个要求。
大臣说:“就在这个棋盘上放些米粒吧。第一格放一粒米,
第二格放两粒米,第三格放4粒米,然后是8粒米、16粒、
32粒、…一直到第64格。”“你真傻!就要这么一点米粒?”
国王哈哈大笑。大臣说:“就怕您的国库里没有这么多米!”
你认为国王的国库里有这么多米吗? 事实上,按照这个大臣的要求,放满一个棋盘上的64个格子需要1+2+22+23+……+263=264-1粒米。 264到底多大呢?
答案是:18 446 744 073 709 551 616读一读
棋盘上的学问 2.如图,一正方体的棱长为a厘米, 则它的体积 为 立方厘米。a×a×a复习回顾 1.如图,边长为a厘米的正方形的面积
为 平方厘米。a×aaa在小学已经知道:a×a=a×a×a=读作:a的平方(或a的二次方)读作:a的立方(或a的三次方) 某种细胞 每30分钟便由一个分裂成两个。经过3小时这种细胞由1个能分裂成多少个?分裂方式如下所示:合作探究:第一次第二次第三次 这个细胞分裂一次可得多少个细胞?
那么,3小时共分裂了多少次?有多少个细胞?答:一次得:
两次 :
三次 :
四次 :2个;2×2个;2×2×2个;六次 : 2×2×2×2×2×2个.分裂两次呢?分裂三次呢?四次呢?做一做:2×2×2×2个 请比较细胞分裂四次后的个数式子:2×2×2×2和细胞分裂六次后的个数式子: 2×2×2×2×2×2.1.这两个式子有什么相同点?答:它们都是乘法;并且它们各自的因数都相同.2.同学们想一想:这样的运算能像平方、立方那样简写吗? 这样的运算我们可以像平方和立方那样简写:2×2×2×22×2×2×2×2×2记作记作一般的,任意多个相同的有理数相乘,我们通常记作:=乘方的意义 这种求n个相同因数a的积的运算叫做乘方,乘方的结果叫做幂,a叫做底数,n叫做指数,an读作a的n次幂(或a的n次方)。 (1次方可省略不写,2次方又叫平方,3次方又叫立方。)获取新知巩固新知:1、(口答)
把下列相同因数的乘积
写成幂的形式,并说出底数和指数:(1) (-6)×(-6) ×(-6)底数是 –6,指数是 3(2)底数是指数是 4温馨提示:幂的底数是分数或负数时,底数应该添上括号!填一填777底数指数-310-3-3102、把 写成几个相同因数相乘的形式3、把(-2)× (-2)× (-2)×···×(-2)10个(-2)写成幂的形式。在不会引起误解的情况下,乘号也可以用“·”表示。例如:(-3)×(-3)×(-3) ×(-3)可写成(-3)·(-3)·(-3)·(-3)7底指12的10次方 底指-3的16次方17对错错错试试你的火眼金睛思考:说说下列各数的意义,它们一样吗?
表示3个2相乘表示2个3相乘试试你的火眼金睛思考:请指出下列幂的底数与指数并说说下列各数的意义,它们一样吗?试试你的火眼金睛思考:说说下列各数的意义,它们一样吗?
要注意哟!对于分数的乘方,负数的乘方,书写时一定要注意小括号,这也是辩认底数的方法. 写出算式=3×3×3×3=81=(-3)×(-3)×(-3)×(-3)=+81写出算式注意符号解题步骤与思路★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★错误的原因是仅将分子乘方,不将分母乘方。注意,应将分数全体乘方。同号两数相乘符号为正=-(4×4)
=-16-号保留不变计算计算(观察各题结果,你能发现乘方运算的符号有什么规律?)
(1)32 24 16
(2)51 23 19
(3)(-9)2 (-2)6 (-3)4
(4)(-2)5 (-3)3 (-1)3
(5)02 03 04 09
有理数乘方的规律
1、正数的任何次幂都是正数
2、负数的偶次幂是正数,负数的奇次幂是负数
3 、零的任何正整数次幂都是零一 不做运算,判断下列各运算结果的符号
(-3)13 (-2)24 (-1.7)2003
-(-2)23 02004 (-3.9)12注意:“一看底数,二看指数”
当底数是正数时,结果为正;当底数是0时,结果是0;
当底数是负数时,再看指数,若指数为偶数,结果为正,
若指数是奇数,结果为负(1) (2)
(3) (4)
(5) (6)
=1=1=-1=1=1=-1口答(1) 1的任何次幂都为 1。(2) -1的奇次幂是-1 ,
-1的偶次幂是1。规律:1001000;100-100010000抢答练习:计算10000(1)正数的任次幂为正;负数的偶次 幂为正
奇次幂为负 0.01;-0.001返回下一张上一张退出抢答练习:计算0.00010.01;0.001;0.0001规律:
(1)正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数。0的任何次幂都是0.
(2)底数绝对值为10的幂的特点:1后面0的个数与指数相同。
(3)底数绝对值为0.1的幂的特点:1前面0的个数与指数相同(包括小数点前的1个零。(1) (2) (3) 1)、计 算达标训练 2) 在94中,底数是 ,指数是 ,读作 ,或读作 ;
3) 在(-2)3中,底数是 ,指数是 ,读作 ,或读作 ;
4) 在 中,底数是 ,指数是 ,读作 ;
5) 在 5 中,底数是 ,指数是 ;
6) 02 = ,03 = , 04 = ;
7)23 = ,24 = , 25 = ;
8)(-3)2 = ,(-3)3 = ,(-3)4 = , (-3)5 = ;猜一猜这节课你学会了一种什么运算?你有何体会?反思“乘方”精神:虽然是简简单单的重复,但结果却是惊人的。做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。(2)负数的乘方,在书写时一定要把整个负数(连同符号),用小括号括起来.分数的乘方,在书写的时一定要把整个分数用 小括号括起来.(1)正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数.同学们
再
见!
