【核心素养目标】2.1认识无理数 教学设计
文档属性
| 名称 | 【核心素养目标】2.1认识无理数 教学设计 |
|
|
| 格式 | docx | ||
| 文件大小 | 878.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-08 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2.1认识无理数教学设计
课题 2.1认识无理数 单元 2 学科 数学 年级 八
教材分析 本节课让学生感受无理数的存在,初步建立无理数的印象,结合勾股定理知识,学生将在具体的实例中,通过操作、分析等活动,感受无理数的客观存在性和引入的必要性,根据正方形的面积拼图活动说明存在着无理数.
核心素养分析 教师引导学生回忆有理数的分类,使学生感受前后所学知识的一致性与连续性。以面积为2的正方形的边长为引言,引入新课。激发学生的探究热情。通过操作让学生感受到无理数的确实存在性。在探究过程中使学生感受数的扩展,体会无理数产生的过程,积累解决数学问题的经验和方法。认识数学与人类的密切联系,体验数学活动充满着探索与创造。在参与对数学问题的讨论时敢于发表自己的观点。
学习 目标 1、通过拼图活动,感受无理数产生的实际背景和引入的必要性。 2、借助计算器探索无理数是无限不循环小数,并从中体会无限逼近的思想。 3、会判断一个数是无理数还是有理数。
重点 会辨别有理数与无理数.
难点 无理数概念的推导过程.
教学过程
教学环节 教师活动 学生活动 设计意图
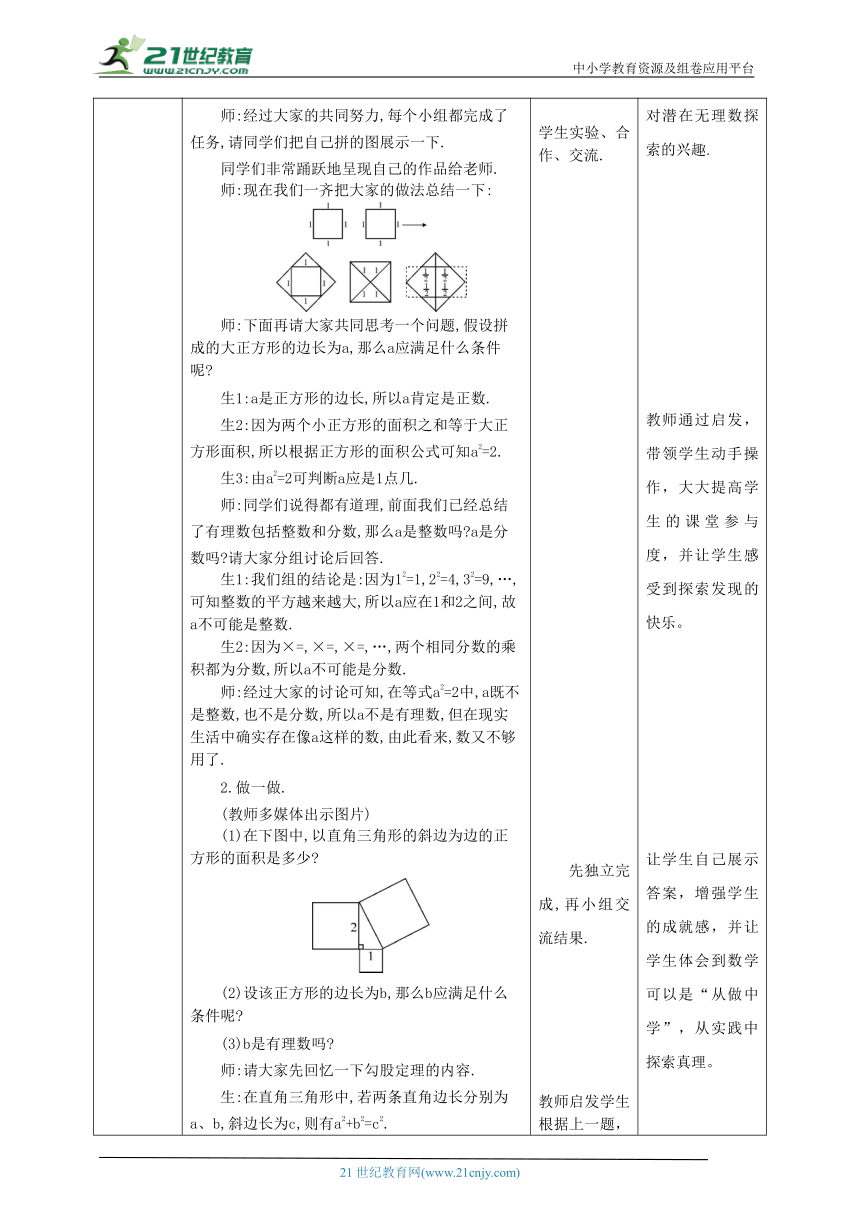
导入新课 师:同学们已经上了好多年的学,学过很多的数,同学们能概括一下都学过哪些数吗 生1:在小学我们学过自然数、小数、分数. 生2:在初一我们还学过负数. 师:对,我们在小学学了非负数,在初一发现数不够用了,引入了负数,即把从小学学过的正数、零扩充到有理数范围,有理数包括整数和分数,那么有理数范围是否就能满足我们实际生活的需要呢 今天这节课我们就来共同研究这个问题. 教师提问勾股定理与勾股定理逆定理知识点,由学生回答。 唤起学生的知识记忆,以便进入新的学习。
讲授新课 1.提出问题. 师:请同学们四个人为一组,拿出自己准备好的两个边长为1的正方形和剪刀,认真讨论之后,动手剪一剪,拼一拼,设法得到一个大的正方形,好吗 生:好! (学生非常高兴地投入到活动中.) 师:经过大家的共同努力,每个小组都完成了任务,请同学们把自己拼的图展示一下. 同学们非常踊跃地呈现自己的作品给老师. 师:现在我们一齐把大家的做法总结一下: 师:下面再请大家共同思考一个问题,假设拼成的大正方形的边长为a,那么a应满足什么条件呢 生1:a是正方形的边长,所以a肯定是正数. 生2:因为两个小正方形的面积之和等于大正方形面积,所以根据正方形的面积公式可知a2=2. 生3:由a2=2可判断a应是1点几. 师:同学们说得都有道理,前面我们已经总结了有理数包括整数和分数,那么a是整数吗 a是分数吗 请大家分组讨论后回答. 生1:我们组的结论是:因为12=1,22=4,32=9,…,可知整数的平方越来越大,所以a应在1和2之间,故a不可能是整数. 生2:因为×=,×=,×=,…,两个相同分数的乘积都为分数,所以a不可能是分数. 师:经过大家的讨论可知,在等式a2=2中,a既不是整数,也不是分数,所以a不是有理数,但在现实生活中确实存在像a这样的数,由此看来,数又不够用了. 2.做一做. (教师多媒体出示图片) (1)在下图中,以直角三角形的斜边为边的正方形的面积是多少 (2)设该正方形的边长为b,那么b应满足什么条件呢 (3)b是有理数吗 师:请大家先回忆一下勾股定理的内容. 生:在直角三角形中,若两条直角边长分别为a、b,斜边长为c,则有a2+b2=c2. 师:在这道道题中,两条直角边长分别为1和2,斜边长为b,根据勾股定理得b2=12+22,即b2=5,那么b是有理数吗 请举手回答. 生1:因为22=4,32=9,22课堂练习 1.下列各数中,是有理数的是( ) A.面积为3的正方形的边长 B.体积为8的正方体的棱长 C.两直角边分别为1和2的直角三角形的斜边长 D.长为3,宽为2的长方形的对角线长 2.下列一组数:-8,2.5,30,π, 0.161616 … ,0.6,0.080 080 008…(相邻两个8之间依次增加一个0),其中无理数有 ( ) A.0个 B.1个 C.2个 D.3个 3.如图,在方格纸中,假设每个小正方形的面积为2,则图中的四条线段中长度是有理数的线段是______________. 4.面积为7的正方形的边长为x.请你回答下列问题: (1)x的整数部分是多少? (2)把x的值精确到十分位时是多少?精确到百分位呢? (3)x是有理数吗?请说明理由. 学生利用所学知识做练习。 从简单的问题入手,运用勾股定理解决问题,让学生在解题过程中掌握勾股定理的应用,达到“学数学,用数学”的目的,进一步培养学生解决问题的能力和推理论证的能力
课堂小结 通过本节课的学习,你们有什么收获? 学生归纳本节所学内容,并体验核心素养的形成。 通过小结让学生理清本节课的知识结构,感受探究过程中乐趣,体验克服困难的过程,树立学习数学的信心。
板书 1.认识无理数 1.剪拼正方形——等积变形思想方法 2.面积对比,利用计算器探索平方数——无限逼近思想方法 3.任何有限小数或无限循环小数都是有理数 4.无限不循环小数称为无理数
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.1认识无理数教学设计
课题 2.1认识无理数 单元 2 学科 数学 年级 八
教材分析 本节课让学生感受无理数的存在,初步建立无理数的印象,结合勾股定理知识,学生将在具体的实例中,通过操作、分析等活动,感受无理数的客观存在性和引入的必要性,根据正方形的面积拼图活动说明存在着无理数.
核心素养分析 教师引导学生回忆有理数的分类,使学生感受前后所学知识的一致性与连续性。以面积为2的正方形的边长为引言,引入新课。激发学生的探究热情。通过操作让学生感受到无理数的确实存在性。在探究过程中使学生感受数的扩展,体会无理数产生的过程,积累解决数学问题的经验和方法。认识数学与人类的密切联系,体验数学活动充满着探索与创造。在参与对数学问题的讨论时敢于发表自己的观点。
学习 目标 1、通过拼图活动,感受无理数产生的实际背景和引入的必要性。 2、借助计算器探索无理数是无限不循环小数,并从中体会无限逼近的思想。 3、会判断一个数是无理数还是有理数。
重点 会辨别有理数与无理数.
难点 无理数概念的推导过程.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 师:同学们已经上了好多年的学,学过很多的数,同学们能概括一下都学过哪些数吗 生1:在小学我们学过自然数、小数、分数. 生2:在初一我们还学过负数. 师:对,我们在小学学了非负数,在初一发现数不够用了,引入了负数,即把从小学学过的正数、零扩充到有理数范围,有理数包括整数和分数,那么有理数范围是否就能满足我们实际生活的需要呢 今天这节课我们就来共同研究这个问题. 教师提问勾股定理与勾股定理逆定理知识点,由学生回答。 唤起学生的知识记忆,以便进入新的学习。
讲授新课 1.提出问题. 师:请同学们四个人为一组,拿出自己准备好的两个边长为1的正方形和剪刀,认真讨论之后,动手剪一剪,拼一拼,设法得到一个大的正方形,好吗 生:好! (学生非常高兴地投入到活动中.) 师:经过大家的共同努力,每个小组都完成了任务,请同学们把自己拼的图展示一下. 同学们非常踊跃地呈现自己的作品给老师. 师:现在我们一齐把大家的做法总结一下: 师:下面再请大家共同思考一个问题,假设拼成的大正方形的边长为a,那么a应满足什么条件呢 生1:a是正方形的边长,所以a肯定是正数. 生2:因为两个小正方形的面积之和等于大正方形面积,所以根据正方形的面积公式可知a2=2. 生3:由a2=2可判断a应是1点几. 师:同学们说得都有道理,前面我们已经总结了有理数包括整数和分数,那么a是整数吗 a是分数吗 请大家分组讨论后回答. 生1:我们组的结论是:因为12=1,22=4,32=9,…,可知整数的平方越来越大,所以a应在1和2之间,故a不可能是整数. 生2:因为×=,×=,×=,…,两个相同分数的乘积都为分数,所以a不可能是分数. 师:经过大家的讨论可知,在等式a2=2中,a既不是整数,也不是分数,所以a不是有理数,但在现实生活中确实存在像a这样的数,由此看来,数又不够用了. 2.做一做. (教师多媒体出示图片) (1)在下图中,以直角三角形的斜边为边的正方形的面积是多少 (2)设该正方形的边长为b,那么b应满足什么条件呢 (3)b是有理数吗 师:请大家先回忆一下勾股定理的内容. 生:在直角三角形中,若两条直角边长分别为a、b,斜边长为c,则有a2+b2=c2. 师:在这道道题中,两条直角边长分别为1和2,斜边长为b,根据勾股定理得b2=12+22,即b2=5,那么b是有理数吗 请举手回答. 生1:因为22=4,32=9,22
课堂小结 通过本节课的学习,你们有什么收获? 学生归纳本节所学内容,并体验核心素养的形成。 通过小结让学生理清本节课的知识结构,感受探究过程中乐趣,体验克服困难的过程,树立学习数学的信心。
板书 1.认识无理数 1.剪拼正方形——等积变形思想方法 2.面积对比,利用计算器探索平方数——无限逼近思想方法 3.任何有限小数或无限循环小数都是有理数 4.无限不循环小数称为无理数
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
