选修1期末考试总复习第1章常用逻辑用语(上传版)[上学期]
文档属性
| 名称 | 选修1期末考试总复习第1章常用逻辑用语(上传版)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 119.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-01-17 08:22:00 | ||
图片预览






文档简介
课件23张PPT。第一章 常用逻辑用语期末总复习 我们把用语言、符号或式子表达的,可以判断真假的陈述句称为命题. 其中判断为真的语句称为真命题,判断为假的语句称为假命题.基本知识 1.什么叫做命题?例1 判断下面的语句是否为命题?若是命题,指出它的真假。(3)x2+x>0.(2)对于任意的实数a,都有a2+1>0.(1)若整数a是素数,则a是奇数.(4)指数函数是增函数吗?“若P, 则q” 的形式 通常,我们把这种形式的命题中的P叫做命题的条件,q叫做结论. 2.什么叫做条件和结论?例2 将下列命题改写成“若P,则q”的形式.
并判断真假;
(1)面积相等的两个三角形全等;
(2)负数的立方是负数;
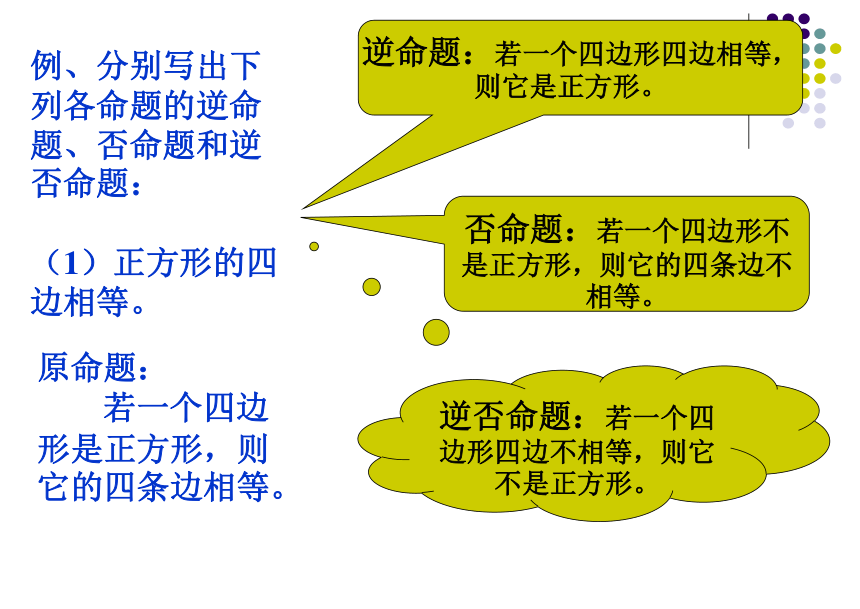
(3)对顶角相等.条件p的否定,记作“? p ”。读作“非p ”。若p 则q逆否命题:原命题:逆命题:否命题:若q 则p若? p 则? q若? q 则? p结论q的否定,记作“? q”。读作“非q”。 3.什么叫做原命题、逆命题、否命题和逆否命题?例、分别写出下列各命题的逆命题、否命题和逆否命题: (1)正方形的四边相等。 逆命题:若一个四边形四边相等,则它是正方形。否命题:若一个四边形不是正方形,则它的四条边不相等。逆否命题:若一个四边形四边不相等,则它不是正方形。
原命题: 若一个四边形是正方形,则它的四条边相等。 结论1:要写出一个命题的另外三个命题关键是分清命题的题设和结论(即把原命题写成“若P则q”的形式)注意:三种命题中最难写 的是否命题。结论2:(1)“或”的否定为“且”,
(2)“且”的否定为“或”,
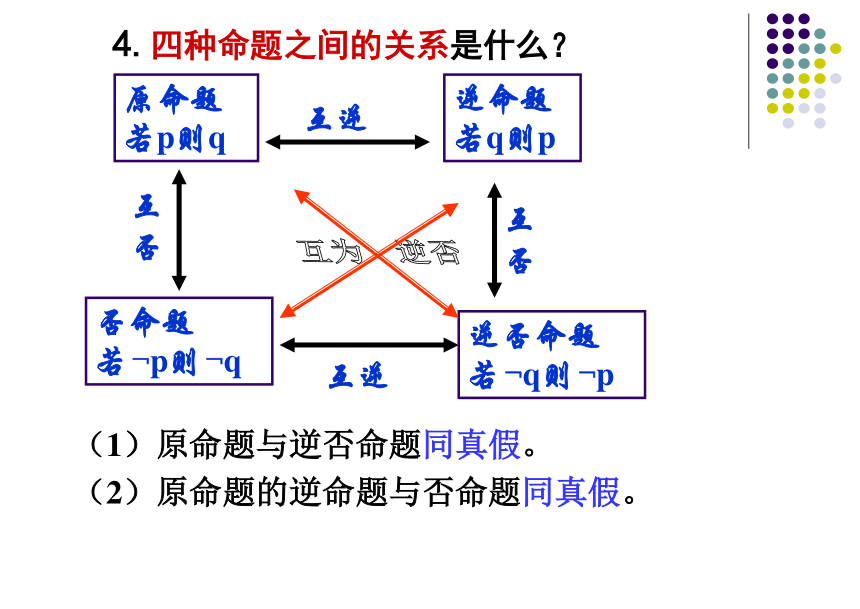
(3)“都”的否定为“不都”。原命题
若p则q逆命题
若q则p否命题
若﹁p则﹁q逆否命题
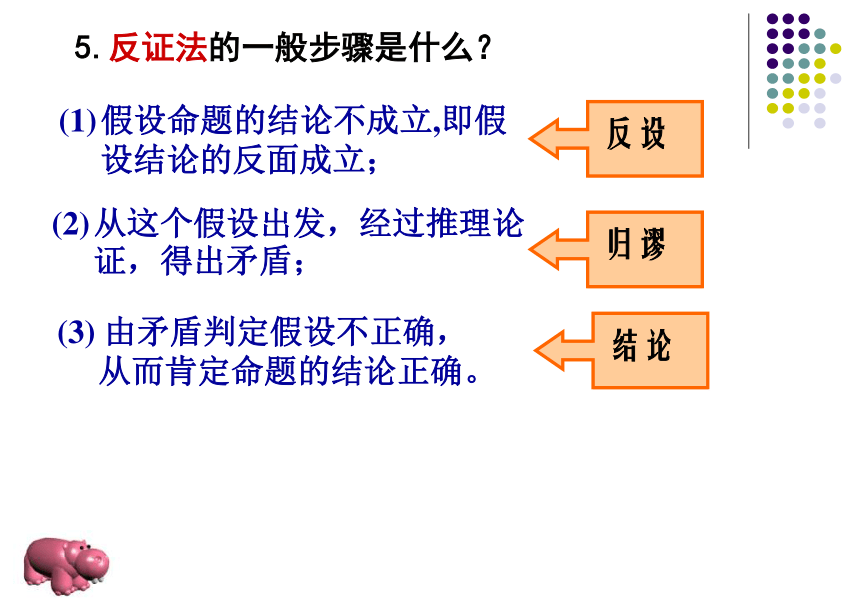
若﹁q则﹁p互逆互否互否互逆互为 逆否 4.四种命题之间的关系是什么?(1)原命题与逆否命题同真假。(2)原命题的逆命题与否命题同真假。假设命题的结论不成立,即假
设结论的反面成立; 从这个假设出发,经过推理论证,得出矛盾; (3) 由矛盾判定假设不正确,
从而肯定命题的结论正确。 5.反证法的一般步骤是什么?已知:△ABC.求证:∠A、∠B、∠C中不能有两个角是直角.简例:证明:一个三角形中不能有两个角是直角. 6. 什么是充分和必要条件?例6:用“充分不必要,必要不充分,充要,既不充分又不必要填空。
1)sinA>sinB是A>B的_________ __ 条件。既不充分又不必要 充要2)在ΔABC中,sinA>sinB是 A>B的
________条件。补充结论:集合与条件1、设集合M={x|x>2},N={x|x<3},
那么”x∈M或x∈N”是“x∈M∩N”的( )
A.充要条件 B必要不充分条件
C充分不必要 D不充分不必要B2、a∈R,|a|<3成立的一个必要不充分条件是( )
A.a<3 B.|a|<2 C.a2<9 D.0,读作”非p”或”p的否定”思考?
如果 为真命题,那么 一定
是真命题吗?反之,如果 为真命题,
那么 一定是真命题吗?例、用否定的形式填空: (1)a > 0;
(2)a ≥0或b<0; (3)a、b都是正数;(4)A是B的子集;a≤0。a< 0且b≥0。a、b不都是正数。A不是B的子集。辨析:否命题和命题的否定写出命题“两直线平行,同位角相等”的否命题和命题的否定。 类似于(3)(4)中的短语“所有的” “任意一个” “任意的” “一切的” “每一个” “任给” 等,在逻辑中通常叫做全称量词符号表示:含有全称量词的命题,叫做全称命题8.什么叫做全称命题? 一般地,将含有变量x的语句用p(x),q(x),r(x)…..表示, 变量x的取值范围用M表示。那么读作:对任意x属于M,有p(x)成立全称命题 “对M中任意一个x,有p(x)成立”1.存在量词:2.特称命题:含有存在量词的命题叫做特称命题.9.什么叫做特称命题?3.特称命题的符号简记:全称命题“存在M中的元素x0,有p(x0)成立”可用符号
简记为:读做“存在M中的元素x0,有p(x0)成立”.期末考试纲要:选择题:基础题2题 中档题1题
常见题型:1.判断给定的语句是否命题
2.判断给定的命题是真是假
3.判断给定的条件是什么条件填空题:基础题1题
常见题型:1. 给定几个命题选出真命题
2.给定一些条件的逻辑关系最后问指 定的条件的逻辑关系解答题:基础题1题
常见题型:
1. 写出给定命题的四种命题并判断它们的真假;
2.通过逻辑关系讨论题目中的参数的范围;
3.证明充要条件
4.反证法
共22分1、已知p,q都是r的必要条件,
s是r的充分条件,q是s的充分条件,则
(1)s是q的什么条件?
(2)r是q的什么条件?
(3)P是q的什么条件?充要条件充要条件必要条件变.若A是B的必要而不充分条件,C是B的充要条件,D是C的充分而不必要条件,那么D是A的________充分不必要条件补充练习3.已知p是q的必要而不充分条件,
那么┐p是┐q的_______________.充分不必要条件4:若┐A是┐B的充要条件,┐C是┐B的充 要条件,则A为C的( )条件
A.充要 B必要不充分
C充分不必要 D不充分不必要A 5:已知关于x的方程
(1-a)x2+(a+2)x-4=0(a∈R).
求:⑴方程有两个正根的充要条件;
⑵方程至少有一个正根的充要条件。【解题回顾】
一是容易漏掉讨论方程二次项系数是否为零,二是只求必要条件忽略验证充分条件.即以所求的必要条件代替充要条件.
并判断真假;
(1)面积相等的两个三角形全等;
(2)负数的立方是负数;
(3)对顶角相等.条件p的否定,记作“? p ”。读作“非p ”。若p 则q逆否命题:原命题:逆命题:否命题:若q 则p若? p 则? q若? q 则? p结论q的否定,记作“? q”。读作“非q”。 3.什么叫做原命题、逆命题、否命题和逆否命题?例、分别写出下列各命题的逆命题、否命题和逆否命题: (1)正方形的四边相等。 逆命题:若一个四边形四边相等,则它是正方形。否命题:若一个四边形不是正方形,则它的四条边不相等。逆否命题:若一个四边形四边不相等,则它不是正方形。
原命题: 若一个四边形是正方形,则它的四条边相等。 结论1:要写出一个命题的另外三个命题关键是分清命题的题设和结论(即把原命题写成“若P则q”的形式)注意:三种命题中最难写 的是否命题。结论2:(1)“或”的否定为“且”,
(2)“且”的否定为“或”,
(3)“都”的否定为“不都”。原命题
若p则q逆命题
若q则p否命题
若﹁p则﹁q逆否命题
若﹁q则﹁p互逆互否互否互逆互为 逆否 4.四种命题之间的关系是什么?(1)原命题与逆否命题同真假。(2)原命题的逆命题与否命题同真假。假设命题的结论不成立,即假
设结论的反面成立; 从这个假设出发,经过推理论证,得出矛盾; (3) 由矛盾判定假设不正确,
从而肯定命题的结论正确。 5.反证法的一般步骤是什么?已知:△ABC.求证:∠A、∠B、∠C中不能有两个角是直角.简例:证明:一个三角形中不能有两个角是直角. 6. 什么是充分和必要条件?例6:用“充分不必要,必要不充分,充要,既不充分又不必要填空。
1)sinA>sinB是A>B的_________ __ 条件。既不充分又不必要 充要2)在ΔABC中,sinA>sinB是 A>B的
________条件。补充结论:集合与条件1、设集合M={x|x>2},N={x|x<3},
那么”x∈M或x∈N”是“x∈M∩N”的( )
A.充要条件 B必要不充分条件
C充分不必要 D不充分不必要B2、a∈R,|a|<3成立的一个必要不充分条件是( )
A.a<3 B.|a|<2 C.a2<9 D.0
如果 为真命题,那么 一定
是真命题吗?反之,如果 为真命题,
那么 一定是真命题吗?例、用否定的形式填空: (1)a > 0;
(2)a ≥0或b<0; (3)a、b都是正数;(4)A是B的子集;a≤0。a< 0且b≥0。a、b不都是正数。A不是B的子集。辨析:否命题和命题的否定写出命题“两直线平行,同位角相等”的否命题和命题的否定。 类似于(3)(4)中的短语“所有的” “任意一个” “任意的” “一切的” “每一个” “任给” 等,在逻辑中通常叫做全称量词符号表示:含有全称量词的命题,叫做全称命题8.什么叫做全称命题? 一般地,将含有变量x的语句用p(x),q(x),r(x)…..表示, 变量x的取值范围用M表示。那么读作:对任意x属于M,有p(x)成立全称命题 “对M中任意一个x,有p(x)成立”1.存在量词:2.特称命题:含有存在量词的命题叫做特称命题.9.什么叫做特称命题?3.特称命题的符号简记:全称命题“存在M中的元素x0,有p(x0)成立”可用符号
简记为:读做“存在M中的元素x0,有p(x0)成立”.期末考试纲要:选择题:基础题2题 中档题1题
常见题型:1.判断给定的语句是否命题
2.判断给定的命题是真是假
3.判断给定的条件是什么条件填空题:基础题1题
常见题型:1. 给定几个命题选出真命题
2.给定一些条件的逻辑关系最后问指 定的条件的逻辑关系解答题:基础题1题
常见题型:
1. 写出给定命题的四种命题并判断它们的真假;
2.通过逻辑关系讨论题目中的参数的范围;
3.证明充要条件
4.反证法
共22分1、已知p,q都是r的必要条件,
s是r的充分条件,q是s的充分条件,则
(1)s是q的什么条件?
(2)r是q的什么条件?
(3)P是q的什么条件?充要条件充要条件必要条件变.若A是B的必要而不充分条件,C是B的充要条件,D是C的充分而不必要条件,那么D是A的________充分不必要条件补充练习3.已知p是q的必要而不充分条件,
那么┐p是┐q的_______________.充分不必要条件4:若┐A是┐B的充要条件,┐C是┐B的充 要条件,则A为C的( )条件
A.充要 B必要不充分
C充分不必要 D不充分不必要A 5:已知关于x的方程
(1-a)x2+(a+2)x-4=0(a∈R).
求:⑴方程有两个正根的充要条件;
⑵方程至少有一个正根的充要条件。【解题回顾】
一是容易漏掉讨论方程二次项系数是否为零,二是只求必要条件忽略验证充分条件.即以所求的必要条件代替充要条件.
