11.2.1.1三角形的内角 课件(38页PPT)
文档属性
| 名称 | 11.2.1.1三角形的内角 课件(38页PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-08 18:13:23 | ||
图片预览








文档简介
(共40张PPT)
11.2.1三角形的内角
人教版八年级上册
第十一章 三角形
教学目标
1、会阐述三角形内角和定理。
2、会应用三角形内角和定理进行计算(求三角形的角的度数)。
3、能通过动手实践去验证三角形的内角和定理。
4、了解直角三角形两个锐角的关系。
5、掌握直角三角形的判定。
6、会运用直角三角形的性质和判定进行相关计算。
新知导入
数 学 故 事
在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结。
可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”
“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了……”
“为什么?”老二很纳闷。
同学们,你们能够帮“老二”解释其中的道理吗?
新知导入
在小学的时候,我们就已经知道,任意一个三角形的内角和等于180°。
在Rt△ABC中,老大∠A=90°,则∠B+∠C=90°
因此老二∠B或∠C<90°。
新知讲解
一、三角形的内角和
任意一个三角形的内角和一定等于 。
180°
验证三角形内角和的三种方法:
测量法
折叠法
剪切法
新知讲解
测量法
锐角三角形
480
720
600
60°+48°+72°=180°
新知讲解
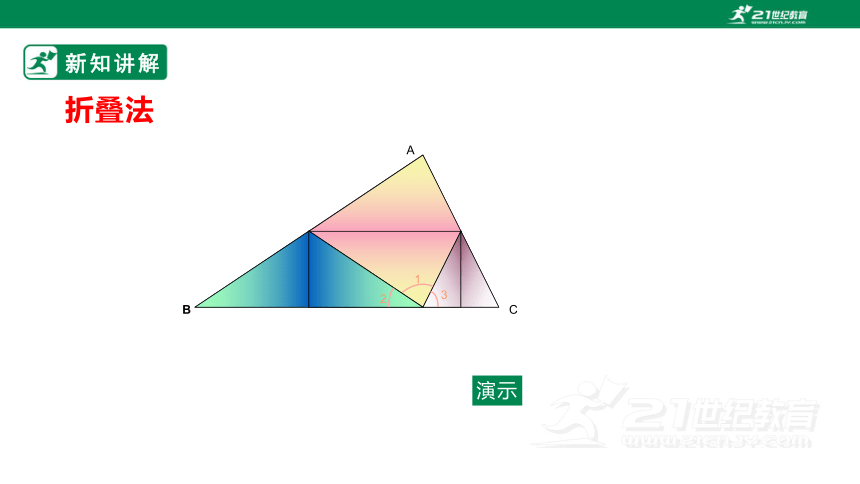
折叠法
A
B
C
演示
1
2
3
新知讲解
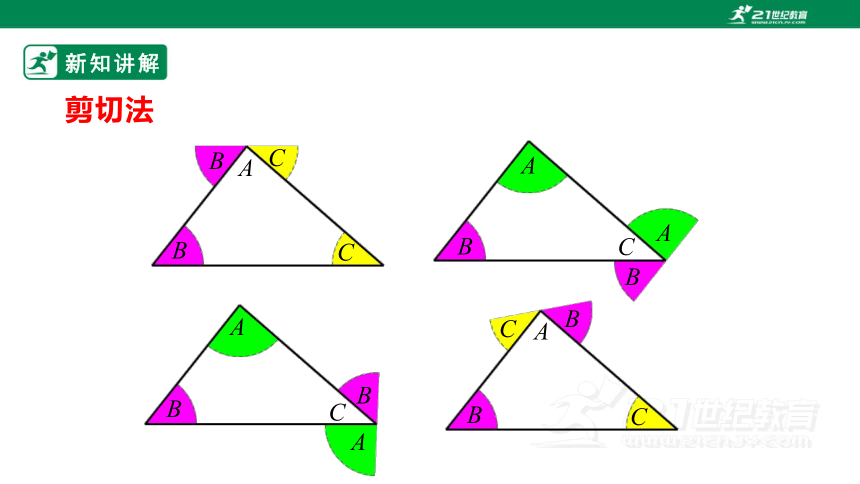
剪切法
B
B
C
C
A
A
A
B
B
C
A
A
B
B
C
A
B
B
C
C
新知讲解
那么,我们如何通过“数学证明”来解释三角形的内角和一定是180°呢?
已知:△ABC
求证:∠A+∠B+∠C=180°
方法一、证明:过点A作直线l,使l∥AB
∵l∥AB
∴∠2=∠4(两直线平行,内错角相等)
同理 ∠3=∠5
∵∠1、∠4、∠5组成平角
∴∠1+∠2+∠3=180°(等量代换)
∴∠A+∠B+∠C=180°(等量代换)
三角形内角和定理:三角形三个内角的和为180°
新知讲解
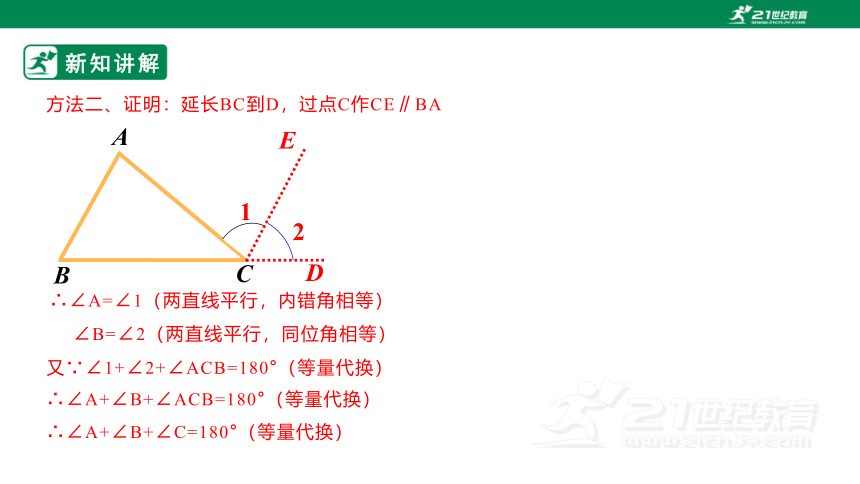
方法二、证明:延长BC到D,过点C作CE∥BA
C
B
A
E
D
1
2
∴∠A=∠1(两直线平行,内错角相等)
∠B=∠2(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°(等量代换)
∴∠A+∠B+∠ACB=180°(等量代换)
∴∠A+∠B+∠C=180°(等量代换)
新知讲解
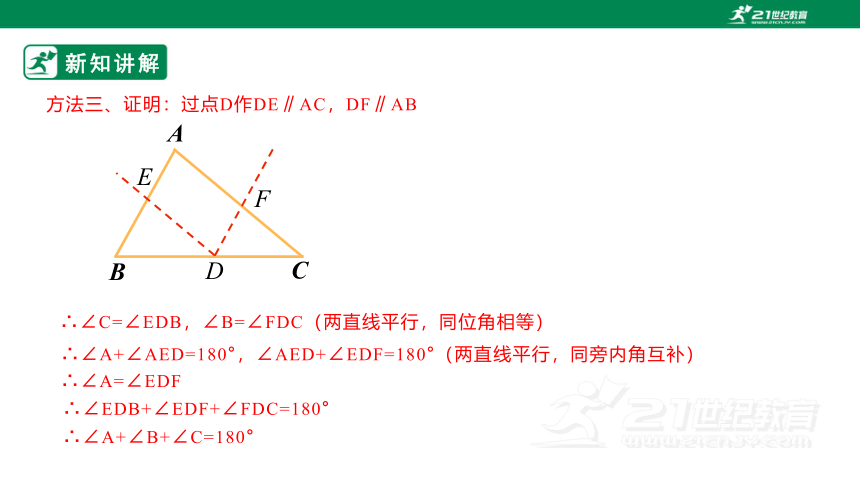
方法三、证明:过点D作DE∥AC,DF∥AB
C
B
A
E
D
F
∴∠C=∠EDB,∠B=∠FDC(两直线平行,同位角相等)
∴∠A+∠AED=180°,∠AED+∠EDF=180°(两直线平行,同旁内角互补)
∴∠A=∠EDF
∴∠EDB+∠EDF+∠FDC=180°
∴∠A+∠B+∠C=180°
新知讲解
例1 如图,在△ABC中, ∠BAC=40 °, ∠B=75 °,AD是△ABC的角平分线,求∠ADB的度数。
A
B
C
D
解:由∠BAC=40 °, AD是△ABC的角平分线,得
∠BAD= ∠BAC=20°
在△ABD中,
∠ADB=180°-∠B-∠BAD
=180°-75°-20°
=85°
∴∠ABD的度数为85°。
新知讲解
例2 如图是A、B、C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80 °方向,C岛在B岛的北偏西40 °方向。从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB是多少度?
分析:A、B、C三岛的连线构成△ABC,所求的∠ACB是△ABC的一个
内角,如果能求出∠CAB、∠ABC,就能求出∠ACB。
解:∠CAB=∠BAD-∠CAD=80°-50°=30°
由AD∥BE,得∠BAD+∠ABE=180°
∴∠ABE=180°-∠ABD=180°-80°=100°
∠ABC=∠ABE-∠EBC=100°-40°=60°
在△ABC中,∠ACB=180°-∠ABC-∠CAB
=180°-60°-30°
= 90°
答:从B岛看A、C两岛的视角∠ABC是60°,
从C岛看A、B两岛的视角∠ACB是90°。
新知讲解
二、直角三角形的性质和判定
如图,在直角三角形ABC中,∠C=90°
由三角形内角和定理,可得∠A+∠B+∠C=180°
∴∠A+∠B+90°=180°
∴∠A+∠B=90
直角三角形的两个锐角互余。
新知讲解
直角三角形可以用符号“Rt△”表示。因此直角三角形ABC可写成 。
Rt△ABC
“直角三角形的两个锐角互余”其几何语言可表示为:
在Rt△ABC中,
∵∠A=90°
∴∠B+∠C=90°
若在三角形中,有两个锐角互余,则该三角形是否就是直角三角形呢?
新知讲解
已知:在△ABC中,∠A与∠B互余。
求证:该三角形为直角三角形
证明:∵∠A与∠B互余
∴∠A+∠B=90°
由三角形内角和定理,可得
∠A+∠B+∠C=180°
∴90°+∠C=180°
∴∠C=90°
∴△ABC为直角三角形
有两个角互余的三角形为直角三角形。
新知讲解
例3、如图,∠C=∠D=90°,AD、BC相交于点E。
∠CAE与∠DBE有什么关系?为什么?
解:∠CAE=∠DBE
在Rt△ACE中,∠CAE=90°-∠AEC
在Rt△BDE中,∠DBE=90°-∠BED
∵∠AEC=∠BED
∴∠CAE=∠DBE
课堂练习
1、(2022·河南周口·八年级期末)若一个三角形的三个内角度数之比1:3:4,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
【解析】∵三角形三个内角度数的比为1:3:4,
∴三个内角分别是
∴该三角形是直角三角形
故选答案选B
B
课堂练习
2、(2022·湖南邵阳·八年级期中)在Rt△ABC中,∠C=90°,∠A=42°,则∠B=( )
A.48° B.58° C.62° D.68°
【解析】∵∠C=90°
∴∠A+∠B=90°
∵∠A=42°
∴∠B=48°
故答案选A
A
课堂练习
3、(2022·广西钦州·八年级期末)如图,把一副三角板叠放在一起。
则∠1的大小为( )
A.105° B.115° C.120° D.125°
∴
【解析】如图
∵图中是一副直角三角板,
∴∠A=45°,∠E=30°
∵
∴
∴
∵
故答案选A
A
课堂练习
4、(2022·安徽滁州·八年级期末)如图,△ABC中,AD是BC边上的高,
AE是∠BAC的平分线,∠BAC=50°,∠ABC=60°,则∠DAE=( )
A.5° B.4° C.8° D.6°
【解析】△ABC中,∠BAC=50°,∠ABC=60°
∴∠C=180°-∠BAC-∠ABC=70°
∵AD是BC边上的高
∴∠ADC=90°
∴∠DAC=90°-∠C=20°
∵AE是∠BAC的平分线,∠BAC=50°
∴∠EAC= ∠BAC=25°
∴∠DAE=∠EAC-∠DAC=25°-20°=5°
A
课堂练习
5、(2022·湖南长沙·八年级期末)已知在△ABC中,∠A=108°,∠B=2∠C,则∠B=________。
【解析】∵∠A= 108°,∠B= 2∠C
∴108°十2∠C +∠C= 180°
∴∠C=24°
∴∠B=2∠C=2×24°=48°
48°
课堂练习
6、(2022·山东临沂·八年级期末)在△ABC中,∠A=40°,∠B=20°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为________。
【解析】①当∠ADC=90°时,如图所示:
∠BCD=90°-∠B
=90°-20°
=70°
②当∠ACD=90°时,如图所示:
∵∠ACB=180°-∠A-∠B
=120°
∴∠BCD=∠ACB-∠ACD
=120°-90°
=30°
70°或30°
课堂练习
7、如图,AB∥CD,AD与BC交于点O,∠C=40°,∠AOB=80°,求∠A的度数。
解:∵AB∥CD,∠C=40°
∴∠B=∠C=40°
∵∠A+∠B+∠AOB=180°
∴∠A=180°-∠AOB-∠B
=180°-80°-40°
=60°
∴∠A的度数为60°
课堂练习
8、(2022·重庆长寿·八年级期末)如图,在△ABC中,∠B=40°,∠C=70°,AD为∠BAC的平分线,AE为BC边上的高,求∠DAE的度数。
解:∵∠B=40°,∠C=70°
∴∠BAC=180°-40°-70°=70°
又∵AD为∠BAC的平分线
∴∠DAC=35°
∵AE⊥BC
∴∠EAC=90°-∠C=20°
∴∠DAE=∠DAC-∠EAC
=35°-20°
=15°
∴∠DAE的度数为15°
课堂总结
在Rt△ABC中,
∵∠A=90°
∴∠B+∠C=90°
在△ABC中,
∵∠A+∠B=90°
∴△ABC为直角三角形
作业布置
1、如图,在△ABC中,∠C=56°,点D在线段BA的延长线上,过点D作DF⊥BC于点F,
若∠FDB=20°,则∠CAB的度数为( )
A.76° B.65° C.56° D.54°
【解析】∵DF⊥BC
∴∠DFB=90°
在△BDE中,∠FDB=20°
∴∠B=180°-90°-20°=70°
在△ABC中,∠C=56°
∴∠CAB=180°-70°-56°=54°
故答案选D
D
作业布置
2、(2021·河南商丘·八年级期末)在直角三角形ABC中,∠A:∠B:∠C=1:m:3,则m的值是( )
A.3 B.4 C.1或3 D.2或4
【解析】设∠A=x°,则∠C=3x°
①当∠C=90°时,3x°=90°
解得 x=30
∴∠A=30°,∠B=90°-30°=60°
∴∠A:∠B=30°:60°=1:2
∴m=2
②当∠B=90°时,∠A+∠C=90°
即x°+3x°=90°
解得 x=22.5
∴∠A=22.5°,∠C=67.5°
∴∠A:∠B=22.5°:90°=1:4
∴m=4
综上,m的 值为2或4
D
作业布置
3、(2022·内蒙古鄂尔多斯·八年级期末)如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,则∠ACB的度数是______。
【解析】根据方向角的定义可得,
∠BAE=45°,∠CAE=15°,∠DBC=80°
∵∠BAE=45°,∠EAC=15°
∴∠BAC=∠BAE+∠EAC=45°+15°=60°
∵AE、DB是正南正北方向
∴BD∥AE
∵∠DBE=∠BAE=45°
又∵∠DBC=80°
∴∠ABC=80°-45°=35°
∴∠ACB=180°-∠ABC-∠BAC=180°-60°-35°=85°
85°
作业布置
4、(2022·重庆巴南·八年级期末)如图,将一张三角形纸片ABC的一角(∠A)折叠,使得点A落在四边形BCDE的外部点A′的位置,且点A′与点C在直线AB的异侧,折痕为DE。已知∠C=90°,∠B=60°,若△A′DE的一边与BC平行,且∠ADE=m°,则m=_________。
【解析】①如图,当A′D∥BC时
∵A′D∥BC
∴∠A′DA=∠C=90°
∴由翻折可知∠A′DE=∠ADE=45°
∴m=45
②如图,当A′E∥BC时
∵A′E∥BC
∴∠A′EF=∠B=60°
∵∠A=90°-∠B=30°
∴由折叠可知∠A=30°
∴∠A′FE=∠DFE=90°
∴∠A′DA=90°-∠A=60°
∴∠A′DE= ∠A′DA=30°
∴m=30
③当DE∥BC时,点A′与点C在直线AB的同侧,不符合题意
综上可知m的值为45或30
45或30
作业布置
5、(2022·黑龙江牡丹江·八年级期末)在△ABC中,AB=AC,将△ABC折叠,使A,B两点重合,折痕所在直线与AC边所在直线的夹角为50°,则∠A的度数为 _____________。
【解析】①如图:
由翻折的性质可知:EF⊥AB,
∴∠A+∠AFE=90°.
∵∠AFE=50°,
∴∠A=90°﹣50°=40°
②如图:
由翻折的性质可知:EF⊥AB
∴∠D+∠DAE=90°
∵折痕所在直线与AC边所在直线的夹角为50°
∴∠EDA=50°
∴∠DAE=90°﹣50°=40°
∴∠BAC=140°
综上,∠A的度数为40°或140°
40°或140°
作业布置
6、(2021·河北·石家庄市藁城区第一中学八年级阶段练习)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=40°,∠2=20°,求∠B的度数。
解:∵AE平分∠BAC
∴∠1=∠EAC=∠EAD+∠2
∴∠EAD=∠1-∠2=40°-20°=20°
在Rt△ABD中
∠B=90°-∠BAD=90°-40°-20°=30°
∴∠B的度数为30°
作业布置
7、(2022·河南商丘·八年级期末)如图,AD平分∠BAC,∠EAD=∠EDA,∠B=54°。
(1)求∠EAC的度数;
(2)若∠CAD:∠E=2:5;求∠E的度数.
解:(1)∵∠EAD=∠EDA
∴∠EAC+∠CAD=∠B+∠BAD
∵AD平分∠BAC
∴∠CAD=∠BAD
∴∠EAC=∠B
∵∠B=54°
∴∠EAC=54°
∴∠EAC的度数为54°
(2)设∠CAD=2x,则∠E=5x,∠DAB=2x
∵∠B=54°
∴∠EDA=∠EAD=2x+54°
∵∠EDA+∠EAD+∠E=180°
∴2x+54°+2x+54°+5x=180°
解得x=8°
∴∠E=5x=40°
∴∠E的度数为40°
作业布置
8、(2022·湖北荆门·八年级期末)如图,△ABC中,AF、BE是角平分线,
它们相交于点O,AD是高,∠C=50°,求∠DAC及∠BOA的度数。
解:∵AD 是高,∠C=50°
∴∠ADC= 90°
∴∠DAC= 90°-50°=40°
∵∠C= 50°
∴∠CAB+∠ABC = 130°
∵AF、BE是角平分线
∴∠BAO+∠ABO= (∠CAB +∠ABC)= ×(180°-50°)= ×130°=65°
∴∠BOA= 180°- 65° = 115°
∴∠DAC的度数为40°,∠BOA的度数为65°
作业布置
9、(2021·全国·八年级单元测试)如图,在△ABC中,∠B=2∠C,AE平分∠BAC交BC于E。
(1)若AD⊥BC于D,∠C=40°,求∠DAE的度数;
(1)解:∵∠C=40°,∠B=2∠C
∴∠B=80°
∴∠BAC=60°
∵AE平分∠BAC
∴∠EAC=30°
∵AD⊥BC
∴∠ADC=90°
∴∠DAC=50°
∴∠DAE=50°﹣30°=20°
∴∠DAE的度数为20°
作业布置
9、(2021·全国·八年级单元测试)如图,在△ABC中,∠B=2∠C,AE平分∠BAC交BC于E。
(2)若EF⊥AE交AC于F,求证:∠C=2∠FEC。
(2)证明:∵EF⊥AE
∴∠AEF=90°
∴∠AED+∠FEC=90°
∵∠DAE+∠AED=90°
∴∠DAE=∠FEC
∵AE平分∠BAC
∴∠EAC= ∠BAC
= (180°﹣∠B﹣∠C)
= (180°﹣3∠C)
=90°﹣ ∠C
∵∠DAE=∠DAC﹣∠EAC
∴∠DAE=∠DAC﹣(90°﹣ ∠C)
=90°﹣∠C﹣90°+ ∠C
= ∠C
∴∠FEC= ∠C
∴∠C=2∠FEC
作业布置
10、(2022·安徽合肥·八年级期末)(1)如图1,在△ABC中,点D、E在边BC上,AD平分∠BAC,AE⊥BC,∠B=35°,∠C=65°,求∠DAE的度数。
(1)解:由题意得:∠BAC=180°-∠B-∠C=180°-35°-65°=80°
∵AD平分∠BAC
∴∠BAD= ∠BAC=40°
∵AE⊥BC
∴∠AEB=90°
∴∠BAE=180°-∠B-∠AEB=55°
∴∠DAE=∠BAE-∠BAD=15°
∴∠DAE的度数为15°
作业布置
10、(2022·安徽合肥·八年级期末) (2)如图2,若把(1)中的条件“AE⊥BC”变成“F为AD上任意一点(不与A、D重合),FE⊥BC”,其它条件不变,求∠DFE的度数。
(2)解:过点A作AH⊥BC于H,如图
由(1)可得∠DAH=15°
∵FE⊥BC
∴AH∥EF
∴∠DFE=∠DAH=15°
∴∠DFE的度数为15°
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
11.2.1三角形的内角
人教版八年级上册
第十一章 三角形
教学目标
1、会阐述三角形内角和定理。
2、会应用三角形内角和定理进行计算(求三角形的角的度数)。
3、能通过动手实践去验证三角形的内角和定理。
4、了解直角三角形两个锐角的关系。
5、掌握直角三角形的判定。
6、会运用直角三角形的性质和判定进行相关计算。
新知导入
数 学 故 事
在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结。
可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”
“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了……”
“为什么?”老二很纳闷。
同学们,你们能够帮“老二”解释其中的道理吗?
新知导入
在小学的时候,我们就已经知道,任意一个三角形的内角和等于180°。
在Rt△ABC中,老大∠A=90°,则∠B+∠C=90°
因此老二∠B或∠C<90°。
新知讲解
一、三角形的内角和
任意一个三角形的内角和一定等于 。
180°
验证三角形内角和的三种方法:
测量法
折叠法
剪切法
新知讲解
测量法
锐角三角形
480
720
600
60°+48°+72°=180°
新知讲解
折叠法
A
B
C
演示
1
2
3
新知讲解
剪切法
B
B
C
C
A
A
A
B
B
C
A
A
B
B
C
A
B
B
C
C
新知讲解
那么,我们如何通过“数学证明”来解释三角形的内角和一定是180°呢?
已知:△ABC
求证:∠A+∠B+∠C=180°
方法一、证明:过点A作直线l,使l∥AB
∵l∥AB
∴∠2=∠4(两直线平行,内错角相等)
同理 ∠3=∠5
∵∠1、∠4、∠5组成平角
∴∠1+∠2+∠3=180°(等量代换)
∴∠A+∠B+∠C=180°(等量代换)
三角形内角和定理:三角形三个内角的和为180°
新知讲解
方法二、证明:延长BC到D,过点C作CE∥BA
C
B
A
E
D
1
2
∴∠A=∠1(两直线平行,内错角相等)
∠B=∠2(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°(等量代换)
∴∠A+∠B+∠ACB=180°(等量代换)
∴∠A+∠B+∠C=180°(等量代换)
新知讲解
方法三、证明:过点D作DE∥AC,DF∥AB
C
B
A
E
D
F
∴∠C=∠EDB,∠B=∠FDC(两直线平行,同位角相等)
∴∠A+∠AED=180°,∠AED+∠EDF=180°(两直线平行,同旁内角互补)
∴∠A=∠EDF
∴∠EDB+∠EDF+∠FDC=180°
∴∠A+∠B+∠C=180°
新知讲解
例1 如图,在△ABC中, ∠BAC=40 °, ∠B=75 °,AD是△ABC的角平分线,求∠ADB的度数。
A
B
C
D
解:由∠BAC=40 °, AD是△ABC的角平分线,得
∠BAD= ∠BAC=20°
在△ABD中,
∠ADB=180°-∠B-∠BAD
=180°-75°-20°
=85°
∴∠ABD的度数为85°。
新知讲解
例2 如图是A、B、C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80 °方向,C岛在B岛的北偏西40 °方向。从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB是多少度?
分析:A、B、C三岛的连线构成△ABC,所求的∠ACB是△ABC的一个
内角,如果能求出∠CAB、∠ABC,就能求出∠ACB。
解:∠CAB=∠BAD-∠CAD=80°-50°=30°
由AD∥BE,得∠BAD+∠ABE=180°
∴∠ABE=180°-∠ABD=180°-80°=100°
∠ABC=∠ABE-∠EBC=100°-40°=60°
在△ABC中,∠ACB=180°-∠ABC-∠CAB
=180°-60°-30°
= 90°
答:从B岛看A、C两岛的视角∠ABC是60°,
从C岛看A、B两岛的视角∠ACB是90°。
新知讲解
二、直角三角形的性质和判定
如图,在直角三角形ABC中,∠C=90°
由三角形内角和定理,可得∠A+∠B+∠C=180°
∴∠A+∠B+90°=180°
∴∠A+∠B=90
直角三角形的两个锐角互余。
新知讲解
直角三角形可以用符号“Rt△”表示。因此直角三角形ABC可写成 。
Rt△ABC
“直角三角形的两个锐角互余”其几何语言可表示为:
在Rt△ABC中,
∵∠A=90°
∴∠B+∠C=90°
若在三角形中,有两个锐角互余,则该三角形是否就是直角三角形呢?
新知讲解
已知:在△ABC中,∠A与∠B互余。
求证:该三角形为直角三角形
证明:∵∠A与∠B互余
∴∠A+∠B=90°
由三角形内角和定理,可得
∠A+∠B+∠C=180°
∴90°+∠C=180°
∴∠C=90°
∴△ABC为直角三角形
有两个角互余的三角形为直角三角形。
新知讲解
例3、如图,∠C=∠D=90°,AD、BC相交于点E。
∠CAE与∠DBE有什么关系?为什么?
解:∠CAE=∠DBE
在Rt△ACE中,∠CAE=90°-∠AEC
在Rt△BDE中,∠DBE=90°-∠BED
∵∠AEC=∠BED
∴∠CAE=∠DBE
课堂练习
1、(2022·河南周口·八年级期末)若一个三角形的三个内角度数之比1:3:4,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
【解析】∵三角形三个内角度数的比为1:3:4,
∴三个内角分别是
∴该三角形是直角三角形
故选答案选B
B
课堂练习
2、(2022·湖南邵阳·八年级期中)在Rt△ABC中,∠C=90°,∠A=42°,则∠B=( )
A.48° B.58° C.62° D.68°
【解析】∵∠C=90°
∴∠A+∠B=90°
∵∠A=42°
∴∠B=48°
故答案选A
A
课堂练习
3、(2022·广西钦州·八年级期末)如图,把一副三角板叠放在一起。
则∠1的大小为( )
A.105° B.115° C.120° D.125°
∴
【解析】如图
∵图中是一副直角三角板,
∴∠A=45°,∠E=30°
∵
∴
∴
∵
故答案选A
A
课堂练习
4、(2022·安徽滁州·八年级期末)如图,△ABC中,AD是BC边上的高,
AE是∠BAC的平分线,∠BAC=50°,∠ABC=60°,则∠DAE=( )
A.5° B.4° C.8° D.6°
【解析】△ABC中,∠BAC=50°,∠ABC=60°
∴∠C=180°-∠BAC-∠ABC=70°
∵AD是BC边上的高
∴∠ADC=90°
∴∠DAC=90°-∠C=20°
∵AE是∠BAC的平分线,∠BAC=50°
∴∠EAC= ∠BAC=25°
∴∠DAE=∠EAC-∠DAC=25°-20°=5°
A
课堂练习
5、(2022·湖南长沙·八年级期末)已知在△ABC中,∠A=108°,∠B=2∠C,则∠B=________。
【解析】∵∠A= 108°,∠B= 2∠C
∴108°十2∠C +∠C= 180°
∴∠C=24°
∴∠B=2∠C=2×24°=48°
48°
课堂练习
6、(2022·山东临沂·八年级期末)在△ABC中,∠A=40°,∠B=20°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为________。
【解析】①当∠ADC=90°时,如图所示:
∠BCD=90°-∠B
=90°-20°
=70°
②当∠ACD=90°时,如图所示:
∵∠ACB=180°-∠A-∠B
=120°
∴∠BCD=∠ACB-∠ACD
=120°-90°
=30°
70°或30°
课堂练习
7、如图,AB∥CD,AD与BC交于点O,∠C=40°,∠AOB=80°,求∠A的度数。
解:∵AB∥CD,∠C=40°
∴∠B=∠C=40°
∵∠A+∠B+∠AOB=180°
∴∠A=180°-∠AOB-∠B
=180°-80°-40°
=60°
∴∠A的度数为60°
课堂练习
8、(2022·重庆长寿·八年级期末)如图,在△ABC中,∠B=40°,∠C=70°,AD为∠BAC的平分线,AE为BC边上的高,求∠DAE的度数。
解:∵∠B=40°,∠C=70°
∴∠BAC=180°-40°-70°=70°
又∵AD为∠BAC的平分线
∴∠DAC=35°
∵AE⊥BC
∴∠EAC=90°-∠C=20°
∴∠DAE=∠DAC-∠EAC
=35°-20°
=15°
∴∠DAE的度数为15°
课堂总结
在Rt△ABC中,
∵∠A=90°
∴∠B+∠C=90°
在△ABC中,
∵∠A+∠B=90°
∴△ABC为直角三角形
作业布置
1、如图,在△ABC中,∠C=56°,点D在线段BA的延长线上,过点D作DF⊥BC于点F,
若∠FDB=20°,则∠CAB的度数为( )
A.76° B.65° C.56° D.54°
【解析】∵DF⊥BC
∴∠DFB=90°
在△BDE中,∠FDB=20°
∴∠B=180°-90°-20°=70°
在△ABC中,∠C=56°
∴∠CAB=180°-70°-56°=54°
故答案选D
D
作业布置
2、(2021·河南商丘·八年级期末)在直角三角形ABC中,∠A:∠B:∠C=1:m:3,则m的值是( )
A.3 B.4 C.1或3 D.2或4
【解析】设∠A=x°,则∠C=3x°
①当∠C=90°时,3x°=90°
解得 x=30
∴∠A=30°,∠B=90°-30°=60°
∴∠A:∠B=30°:60°=1:2
∴m=2
②当∠B=90°时,∠A+∠C=90°
即x°+3x°=90°
解得 x=22.5
∴∠A=22.5°,∠C=67.5°
∴∠A:∠B=22.5°:90°=1:4
∴m=4
综上,m的 值为2或4
D
作业布置
3、(2022·内蒙古鄂尔多斯·八年级期末)如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,则∠ACB的度数是______。
【解析】根据方向角的定义可得,
∠BAE=45°,∠CAE=15°,∠DBC=80°
∵∠BAE=45°,∠EAC=15°
∴∠BAC=∠BAE+∠EAC=45°+15°=60°
∵AE、DB是正南正北方向
∴BD∥AE
∵∠DBE=∠BAE=45°
又∵∠DBC=80°
∴∠ABC=80°-45°=35°
∴∠ACB=180°-∠ABC-∠BAC=180°-60°-35°=85°
85°
作业布置
4、(2022·重庆巴南·八年级期末)如图,将一张三角形纸片ABC的一角(∠A)折叠,使得点A落在四边形BCDE的外部点A′的位置,且点A′与点C在直线AB的异侧,折痕为DE。已知∠C=90°,∠B=60°,若△A′DE的一边与BC平行,且∠ADE=m°,则m=_________。
【解析】①如图,当A′D∥BC时
∵A′D∥BC
∴∠A′DA=∠C=90°
∴由翻折可知∠A′DE=∠ADE=45°
∴m=45
②如图,当A′E∥BC时
∵A′E∥BC
∴∠A′EF=∠B=60°
∵∠A=90°-∠B=30°
∴由折叠可知∠A=30°
∴∠A′FE=∠DFE=90°
∴∠A′DA=90°-∠A=60°
∴∠A′DE= ∠A′DA=30°
∴m=30
③当DE∥BC时,点A′与点C在直线AB的同侧,不符合题意
综上可知m的值为45或30
45或30
作业布置
5、(2022·黑龙江牡丹江·八年级期末)在△ABC中,AB=AC,将△ABC折叠,使A,B两点重合,折痕所在直线与AC边所在直线的夹角为50°,则∠A的度数为 _____________。
【解析】①如图:
由翻折的性质可知:EF⊥AB,
∴∠A+∠AFE=90°.
∵∠AFE=50°,
∴∠A=90°﹣50°=40°
②如图:
由翻折的性质可知:EF⊥AB
∴∠D+∠DAE=90°
∵折痕所在直线与AC边所在直线的夹角为50°
∴∠EDA=50°
∴∠DAE=90°﹣50°=40°
∴∠BAC=140°
综上,∠A的度数为40°或140°
40°或140°
作业布置
6、(2021·河北·石家庄市藁城区第一中学八年级阶段练习)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=40°,∠2=20°,求∠B的度数。
解:∵AE平分∠BAC
∴∠1=∠EAC=∠EAD+∠2
∴∠EAD=∠1-∠2=40°-20°=20°
在Rt△ABD中
∠B=90°-∠BAD=90°-40°-20°=30°
∴∠B的度数为30°
作业布置
7、(2022·河南商丘·八年级期末)如图,AD平分∠BAC,∠EAD=∠EDA,∠B=54°。
(1)求∠EAC的度数;
(2)若∠CAD:∠E=2:5;求∠E的度数.
解:(1)∵∠EAD=∠EDA
∴∠EAC+∠CAD=∠B+∠BAD
∵AD平分∠BAC
∴∠CAD=∠BAD
∴∠EAC=∠B
∵∠B=54°
∴∠EAC=54°
∴∠EAC的度数为54°
(2)设∠CAD=2x,则∠E=5x,∠DAB=2x
∵∠B=54°
∴∠EDA=∠EAD=2x+54°
∵∠EDA+∠EAD+∠E=180°
∴2x+54°+2x+54°+5x=180°
解得x=8°
∴∠E=5x=40°
∴∠E的度数为40°
作业布置
8、(2022·湖北荆门·八年级期末)如图,△ABC中,AF、BE是角平分线,
它们相交于点O,AD是高,∠C=50°,求∠DAC及∠BOA的度数。
解:∵AD 是高,∠C=50°
∴∠ADC= 90°
∴∠DAC= 90°-50°=40°
∵∠C= 50°
∴∠CAB+∠ABC = 130°
∵AF、BE是角平分线
∴∠BAO+∠ABO= (∠CAB +∠ABC)= ×(180°-50°)= ×130°=65°
∴∠BOA= 180°- 65° = 115°
∴∠DAC的度数为40°,∠BOA的度数为65°
作业布置
9、(2021·全国·八年级单元测试)如图,在△ABC中,∠B=2∠C,AE平分∠BAC交BC于E。
(1)若AD⊥BC于D,∠C=40°,求∠DAE的度数;
(1)解:∵∠C=40°,∠B=2∠C
∴∠B=80°
∴∠BAC=60°
∵AE平分∠BAC
∴∠EAC=30°
∵AD⊥BC
∴∠ADC=90°
∴∠DAC=50°
∴∠DAE=50°﹣30°=20°
∴∠DAE的度数为20°
作业布置
9、(2021·全国·八年级单元测试)如图,在△ABC中,∠B=2∠C,AE平分∠BAC交BC于E。
(2)若EF⊥AE交AC于F,求证:∠C=2∠FEC。
(2)证明:∵EF⊥AE
∴∠AEF=90°
∴∠AED+∠FEC=90°
∵∠DAE+∠AED=90°
∴∠DAE=∠FEC
∵AE平分∠BAC
∴∠EAC= ∠BAC
= (180°﹣∠B﹣∠C)
= (180°﹣3∠C)
=90°﹣ ∠C
∵∠DAE=∠DAC﹣∠EAC
∴∠DAE=∠DAC﹣(90°﹣ ∠C)
=90°﹣∠C﹣90°+ ∠C
= ∠C
∴∠FEC= ∠C
∴∠C=2∠FEC
作业布置
10、(2022·安徽合肥·八年级期末)(1)如图1,在△ABC中,点D、E在边BC上,AD平分∠BAC,AE⊥BC,∠B=35°,∠C=65°,求∠DAE的度数。
(1)解:由题意得:∠BAC=180°-∠B-∠C=180°-35°-65°=80°
∵AD平分∠BAC
∴∠BAD= ∠BAC=40°
∵AE⊥BC
∴∠AEB=90°
∴∠BAE=180°-∠B-∠AEB=55°
∴∠DAE=∠BAE-∠BAD=15°
∴∠DAE的度数为15°
作业布置
10、(2022·安徽合肥·八年级期末) (2)如图2,若把(1)中的条件“AE⊥BC”变成“F为AD上任意一点(不与A、D重合),FE⊥BC”,其它条件不变,求∠DFE的度数。
(2)解:过点A作AH⊥BC于H,如图
由(1)可得∠DAH=15°
∵FE⊥BC
∴AH∥EF
∴∠DFE=∠DAH=15°
∴∠DFE的度数为15°
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
