浙教版科学2022-2023学年上学期九年级“一课一练”:3.4简单的机械(3)--斜面及机械效率【word,含解析】
文档属性
| 名称 | 浙教版科学2022-2023学年上学期九年级“一课一练”:3.4简单的机械(3)--斜面及机械效率【word,含解析】 |  | |
| 格式 | doc | ||
| 文件大小 | 643.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2022-09-09 10:46:44 | ||
图片预览

文档简介
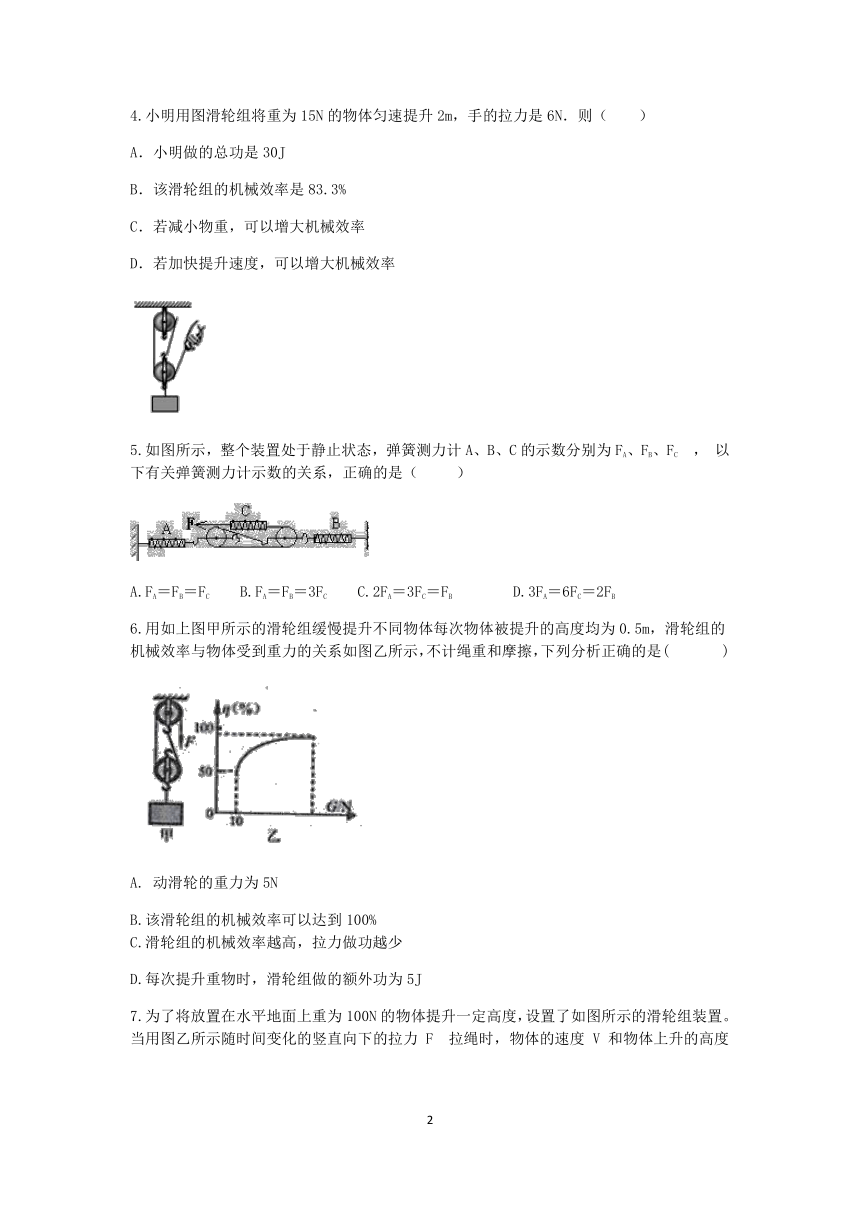
1.如图所示是两个斜面,这两个斜面的粗糙程度相同且等高,现在有 2 个相同的木块在斜面的最高点由静止释放(重心到水平桌面的距离相等),W 为木块重力做功,η 为木块做功的机械效率,下列判断正确的是( )
A. W左图=W右图 ,η左图<η右图 B. W左图=W右图 ,η左图>η右图
C. W左图>W右图 ,η左图=η右图 D. W左图>W右图 ,η左图<η右图
2.如图所示,张伟回学利用斜面,用平行于斜面F=200N的推力,将质量为30kg的物体在5s时间内匀速推到1m高的平台上。斜面长s=2m,g取10N/kg,则( )
A.张伟所做的有用功为400J B.张伟所做的总功为700J
C.张伟的做功功率为140W D.斜面的机械效率为75%
3.小科用如图所示的滑轮组提升G为600N的重物,在绳子自由端施加F为250N的拉力,使重物在4s内匀速上升1m,不计绳重和摩擦。下列说法正确的是( )
A.动滑轮重100N B.拉力做功的功率为150W
C.绳子自由端移动的距离为2m D.此过程滑轮组的机械效率为80%
4.小明用图滑轮组将重为15N的物体匀速提升2m,手的拉力是6N.则( )
A.小明做的总功是30J
B.该滑轮组的机械效率是83.3%
C.若减小物重,可以增大机械效率
D.若加快提升速度,可以增大机械效率
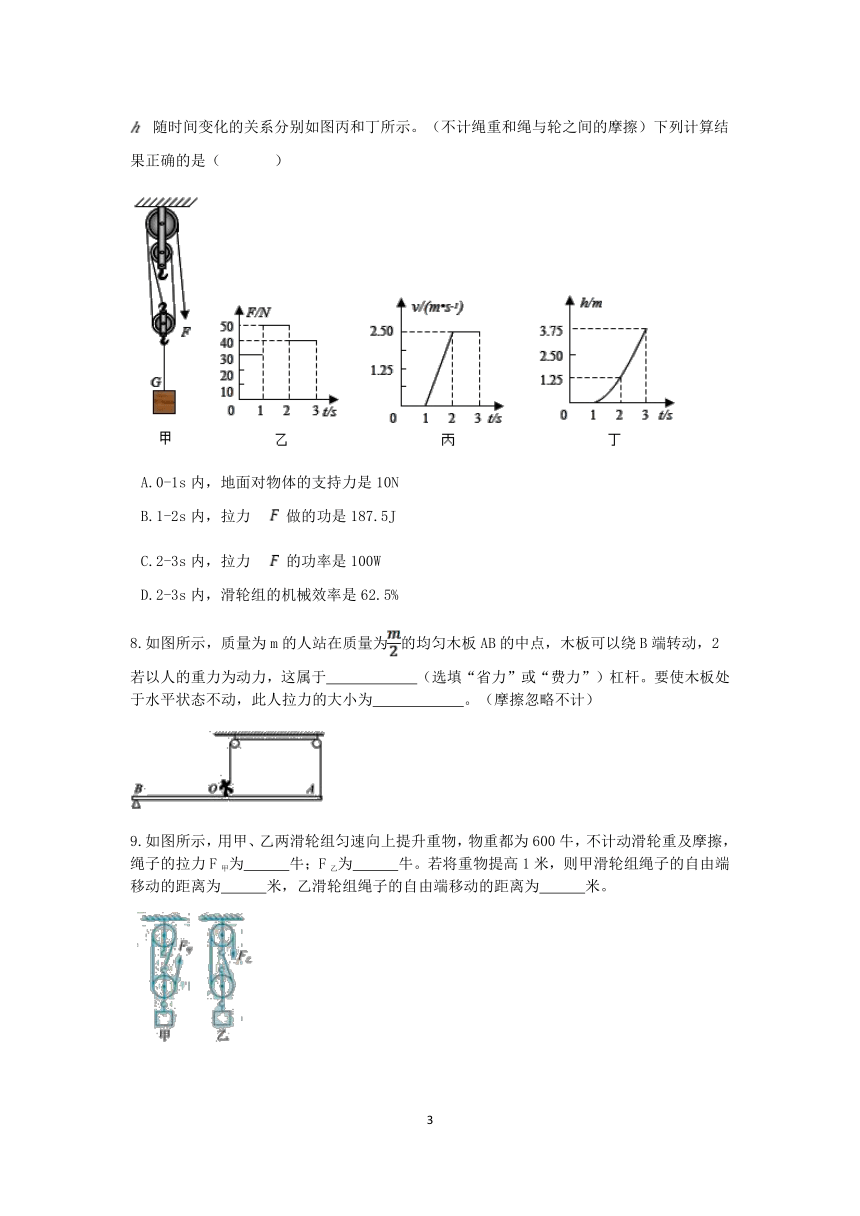
5.如图所示,整个装置处于静止状态,弹簧测力计A、B、C的示数分别为FA、FB、FC , 以下有关弹簧测力计示数的关系,正确的是( )
A.FA=FB=FC B.FA=FB=3FC C.2FA=3FC=FB D.3FA=6FC=2FB
6.用如上图甲所示的滑轮组缓慢提升不同物体每次物体被提升的高度均为0.5m,滑轮组的机械效率与物体受到重力的关系如图乙所示,不计绳重和摩擦,下列分析正确的是( )
动滑轮的重力为5N
B.该滑轮组的机械效率可以达到100%
C.滑轮组的机械效率越高,拉力做功越少
D.每次提升重物时,滑轮组做的额外功为5J
7.为了将放置在水平地面上重为100N的物体提升一定高度,设置了如图所示的滑轮组装置。当用图乙所示随时间变化的竖直向下的拉力 F 拉绳时,物体的速度 V 和物体上升的高度 随时间变化的关系分别如图丙和丁所示。(不计绳重和绳与轮之间的摩擦)下列计算结果正确的是( )
A.0-1s内,地面对物体的支持力是10N
B.1-2s内,拉力 做的功是187.5J
C.2-3s内,拉力 的功率是100W
D.2-3s内,滑轮组的机械效率是62.5%
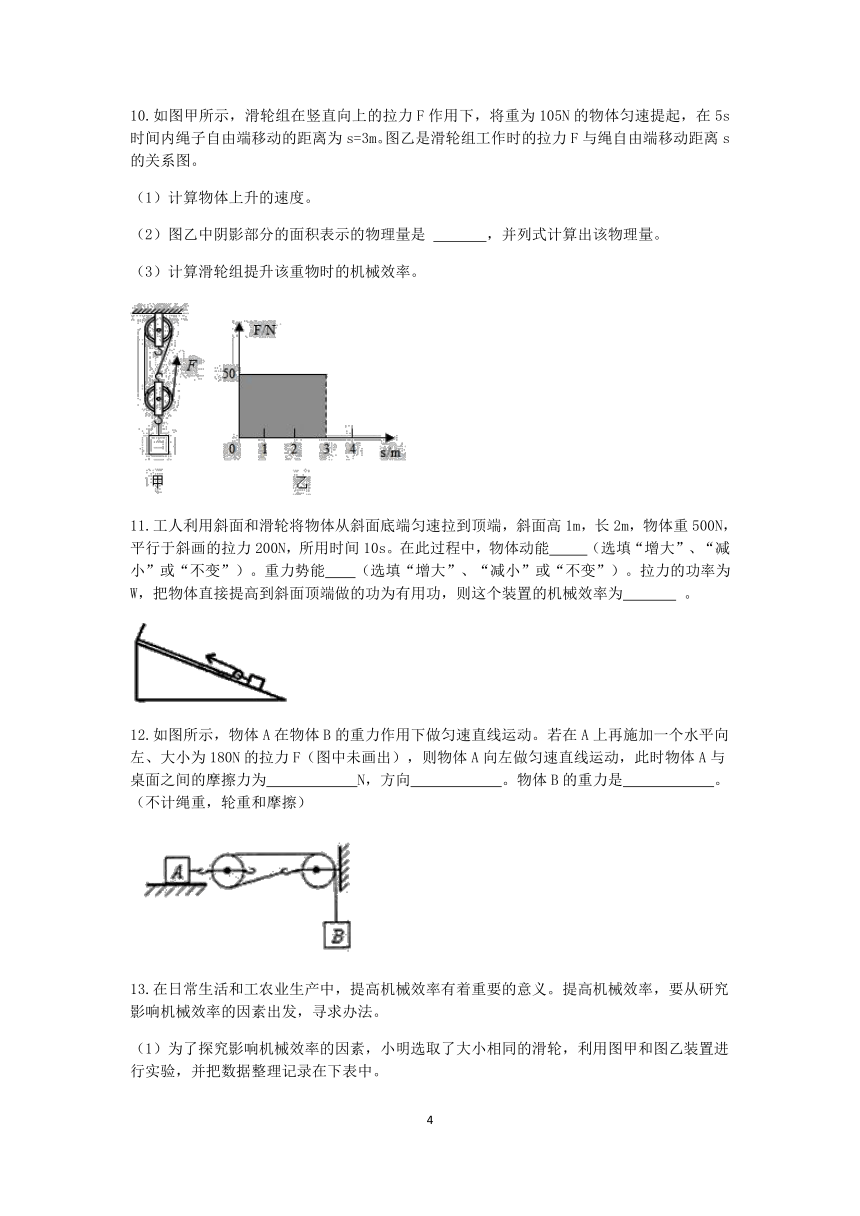
8.如图所示,质量为m的人站在质量为的均匀木板AB的中点,木板可以绕B端转动,2若以人的重力为动力,这属于 (选填“省力”或“费力”)杠杆。要使木板处于水平状态不动,此人拉力的大小为 。(摩擦忽略不计)
9.如图所示,用甲、乙两滑轮组匀速向上提升重物,物重都为600牛,不计动滑轮重及摩擦,绳子的拉力F甲为 牛;F乙为 牛。若将重物提高1米,则甲滑轮组绳子的自由端移动的距离为 米,乙滑轮组绳子的自由端移动的距离为 米。
10.如图甲所示,滑轮组在竖直向上的拉力F作用下,将重为105N的物体匀速提起,在5s时间内绳子自由端移动的距离为s=3m。图乙是滑轮组工作时的拉力F与绳自由端移动距离s的关系图。
(1)计算物体上升的速度。
(2)图乙中阴影部分的面积表示的物理量是 ,并列式计算出该物理量。
(3)计算滑轮组提升该重物时的机械效率。
11.工人利用斜面和滑轮将物体从斜面底端匀速拉到顶端,斜面高1m,长2m,物体重500N,平行于斜画的拉力200N,所用时间10s。在此过程中,物体动能 (选填“增大”、“减小”或“不变”)。重力势能 (选填“增大”、“减小”或“不变”)。拉力的功率为 W,把物体直接提高到斜面顶端做的功为有用功,则这个装置的机械效率为 。
12.如图所示,物体A在物体B的重力作用下做匀速直线运动。若在A上再施加一个水平向左、大小为180N的拉力F(图中未画出),则物体A向左做匀速直线运动,此时物体A与桌面之间的摩擦力为 N,方向 。物体B的重力是 。(不计绳重,轮重和摩擦)
13.在日常生活和工农业生产中,提高机械效率有着重要的意义。提高机械效率,要从研究影响机械效率的因素出发,寻求办法。
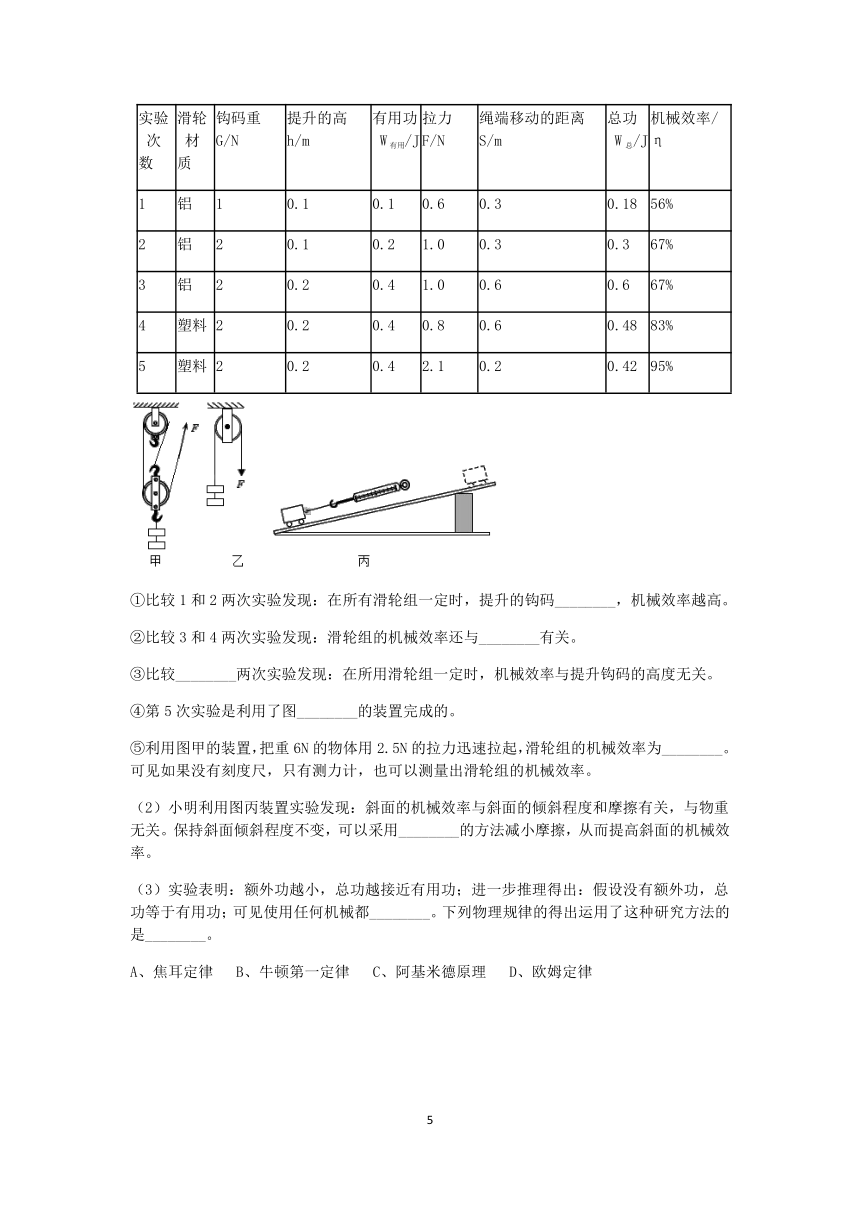
(1)为了探究影响机械效率的因素,小明选取了大小相同的滑轮,利用图甲和图乙装置进行实验,并把数据整理记录在下表中。
实验
次数 滑轮
材质 钩码重G/N 提升的高h/m 有用功
W有用/J 拉力F/N 绳端移动的距离S/m 总功
W总/J 机械效率/η
1 铝 1 0.1 0.1 0.6 0.3 0.18 56%
2 铝 2 0.1 0.2 1.0 0.3 0.3 67%
3 铝 2 0.2 0.4 1.0 0.6 0.6 67%
4 塑料 2 0.2 0.4 0.8 0.6 0.48 83%
5 塑料 2 0.2 0.4 2.1 0.2 0.42 95%
①比较1和2两次实验发现:在所有滑轮组一定时,提升的钩码________,机械效率越高。
②比较3和4两次实验发现:滑轮组的机械效率还与________有关。
③比较________两次实验发现:在所用滑轮组一定时,机械效率与提升钩码的高度无关。
④第5次实验是利用了图________的装置完成的。
⑤利用图甲的装置,把重6N的物体用2.5N的拉力迅速拉起,滑轮组的机械效率为________。可见如果没有刻度尺,只有测力计,也可以测量出滑轮组的机械效率。
(2)小明利用图丙装置实验发现:斜面的机械效率与斜面的倾斜程度和摩擦有关,与物重无关。保持斜面倾斜程度不变,可以采用________的方法减小摩擦,从而提高斜面的机械效率。
(3)实验表明:额外功越小,总功越接近有用功;进一步推理得出:假设没有额外功,总功等于有用功;可见使用任何机械都________。下列物理规律的得出运用了这种研究方法的是________。
A、焦耳定律 B、牛顿第一定律 C、阿基米德原理 D、欧姆定律
14.人们利用如图所示的滑轮组将浸没在河底的实心物体A打捞上来,物体A的密度为9.0×103kg/m3 , 体积为100dm3。在5000N的拉力F作用下,物体A在2s内匀速竖直上升2m(物体未露出水面),不计水的阻力,g取10N/kg,ρ水=1.0×103kg/m3。求:
(1).物体A受到的浮力。
(2).拉力F做功的功率。
(3).滑轮组的机械效率。
15.如图所示,是建筑工人从竖直深井中提取泥土时利用的滑轮组模型。如果某次操作中,工人用400N的拉力F在1分钟内将总重为900N的泥土匀速提升5m。在这段时间内拉力F移动的距离是15m。求:
(1)请根据情景在图中画出滑轮组的绕线方法。
(2)滑轮组的机械效率是多大?
(3)此时动滑轮的重量为多少N?(不考虑各种摩擦及绳重)
答案及解析
1.【答案】 A
【解答】木块的重力相等,斜面的高度相同,根据W有=Gh可知,木块克服重力做功相等,
即W左图=W右图。左图斜面的倾斜角度小于右图, 则木块对左边斜面的压力大于右图斜面,
那么左边斜面产生的摩擦力大于右图斜面;且左边斜面的长度大于右图斜面;
根据W额=fs可知,克服摩擦做的额外功W额左>W额右;
根据可知,左边的机械效率小于右边的机械效率; 即η左图<η右图。
2.【答案】D。
【解析】A、物体的重力:G=mg=30kg×10N/kg=300N,
张伟做的有用功:W有用=Gh=300N×1m=300J,故A错;
B、张伟做的总功:W总=Fs=200N×2m=400J,故B错;
C、张伟的做功功率:,故C错;
(4)斜面的机械效率:
3.【答案】D
【解析】A.根据公式得到:,解得:G动=150N,故A错误;
BC.拉力移动的距离s=nh=1m×3=3m,拉力的速度,拉力的功率P=Fv=250N×0.75m/s=187.5W,故B、C错误;
D.滑轮组的机械效率,故D正确。
4.【答案】B
【解析】A、由图可知n=3,拉力端移动的距离s=3h=3×2m=6m;
小明所做的总功:
W总=Fs=6N×6m=36J;故A错;
B、所做的有用功:W有用=Gh=15N×2m=30J;
滑轮组的机械效率:
C、若减小提升的物重,有用功减小、而额外功几乎不变,有用功与总功的比值减小,机械效率减小,故C错;
D、若加快提升速度,可以增大做功的功率,但有用功与总功的比值不变,不会增大机械效率,故D错。
5.【答案】 D
【解析】分别对左边的滑轮和右边的滑轮进行受力分析,根据二力平衡的知识计算出几个拉力之间的关系即可。
【解答】测力计C直接与绳子相连,则绳子上产生的拉力都是FC。
①以左边的滑轮为对象进行分析,它左边受到A测力计的拉力FA , 右边受到两根绳子的拉力,都是FC。根据二力平衡的知识得到:FA=2FC , 即3FA=6FC;
②以右边的滑轮为对象进行分析,它左边受到绳子的拉力三个,都是FC , 右边受到B测力计的拉力FB。根据二力平衡的知识得到:3FC=FB , 即6FC=2FB。
那么得到:3FA=6FC=2FB。
故选D。
6.【答案】D
【解析】(1)不计绳重和摩擦,根据滑轮组的机械效率,计算动滑轮的重力;
(2)使用滑轮组时,需要提升动滑轮做额外功,据此分析机械效率的数值范围;
(3)根据机械效率的定义分析判断;
(4)克服动滑轮的重力做额外功,即W额=G动h。
【解答】A.由图乙可知,提升物重G=10N时,滑轮组的机械效率η=50%,
不计绳重和摩擦,根据滑轮组的机械效率得到:;
解得:G动=10N,故A错误;
B.使用滑轮组时,需要提升动滑轮做额外功,使得有用功小于总功,滑轮组的机械效率总小于100%,故B错误;
C.滑轮组的机械效率越高,说明有用功与总功的比值越大,拉力做功不一定少,故C错误;
D.利用滑轮组每次物体被提升的高度均为0.5m,提升动滑轮上升的高度也都是0.5m,则每次提升重物时,滑轮组做的额外功都为:W额=G动h=10N×0.5m=5J,故D正确。
7.【答案】B
【解析】由滑轮组的结构可以看出,承担物重的绳子股数n=3,则拉力F移动的距离s=3h。
(1)将滑轮组和物体看做一个整体,根据二力平衡的知识列出平衡关系式,结合滑轮组的工作特点计算出地面对物体的支持力;
(2)根据图像确定2~3s内拉力F的数值和物体运动的速度,结合滑轮组的特点计算出自由端移动的速度,最后根据P=Fv计算出拉力做功的功率;
(3)使用滑轮组提升重物时,根据公式计算出机械效率;
(4)由F-t图象得出在1~2s内的拉力F,由h-t图象得出重物上升的高度,求出拉力F的作用点下降的距离,利用W=Fs求此时拉力做功。
根据图丙可知,0~1s内,物体运动的速度为0,即在地面上保持静止状态。
由图乙可知,在0~1s内,拉力F=30N.取动滑轮和重物为研究对象,受到向下的重力G和G动,向上的支持力F支,及三根绳子向上的拉力F′作用,根据二力平衡的知识得到,
地面对重物的支持力F支=G+G动-3F拉=100N+G动-3×30N=G动+10N,故A错误;
由图丙可知,在2~3s内,重物做匀速运动,此时的速度v3=2.50m/s,拉力F3=40N,
拉力F的作用点下降的速度v3′=3v3=3×2.50m/s=7.5m/s,
拉力做功功率P总=F3V3′=40N×7.5m/s=300W,故C错误;
滑轮组的机械效率:,故D错误;
在1~2s内,拉力F2=50N,重物上升高度h2=1.25m
拉力F的作用点下降的距离s2=3h2=3×1.25m=3.75m,
拉力做的功:W=F2S2=50N×3.75m=187.5J,故B正确。故选B。
8.【答案】 费力;
【解析】(1)比较动力臂和阻力臂的大小,从而确定杠杆的分类;
(2)根据杠杆的平衡条件F1L1=F2L2计算即可。
【解答】(1)根据图片可知,如果将人的重力看做动力,则动力臂为;绳子的拉力看做阻力,阻力臂为AB。此时动力臂小于阻力臂,为费力杠杆。
(2)根据图片可知,B点为支点,阻力为绳子上的拉力FA ,
而动力F1=G人+G木板-FA==mg-FA;
根据杠杆的平衡条件F1L1=F2L2得到:(mg-FA)×=FA×AB;
则此人的拉力FA=。
9.【答案】200;300;3;2
【解析】(1)根据甲图可知,承担重力的绳子段数n=3,则自由端的拉力。根据乙图可知,承担重力的绳子段数n=2,则自由端的拉力;
(2)甲滑轮组绳子自由端移动的距离s甲=n甲h=3×1m=3m;乙滑轮组绳子自由端移动的距离s乙=n乙h=2×1m=2m。
10.【答案】(1)物体上升的速度0.2m/s。
(2)图乙中阴影部分的面积表示的物理量是功,功的大小为150J。
(3)滑轮组提升该重物时的机械效率为70%。
【解析】(1)滑轮组由三段绳子承担总重,s=3h,,
物体上升的速度
纵坐标表示力的大小为50N,大小不变,横坐标表示距离,大小为3m,
所以阴影部分表示力所做的功W=Fs=50N×3m=150J;
(3)滑轮组的机械效率
11.【答案】不变;增大;80;62.5%。
【解析】(1)将物体从斜面底端匀速拉到顶端,质量不变,速度不变,则物体的动能不变。
(2)物体沿斜面升高,质量不变,高度变大,所以其重力势能增大。
(3)图中滑轮是动滑轮,则绳端通过的距离为:s=2L=2×2m=4m;
拉力做功为:W总=Fs=200N×4m=800J;
拉力的功率为:
(4)此过程的有用功为:W有=Gh=500N×1m=500J;
这个装置的机械效率为:62.5%
12.【答案】 90;水平向右;45N
【解析】(1)物体A在物体B的重力作用下向右做匀速直线运动,这时A受到的摩擦力等于动滑轮的拉力,即f=F动;当物体A向左做匀速直线运动时,分析A的受力情况,列出受力平衡式,进而求出A受到的摩擦力和动滑轮上受到的拉力F动。
(2)动滑轮上有2段绳子承担拉力,那么动滑轮上受到的拉力和物体B的重力的关系为:F动=2GB , 据此物体B的重力。
【解答】(1)物体A在物体B的重力作用下向右做匀速直线运动时,
则A受到的摩擦力等于动滑轮对A的拉力,即f=F动;
当物体A向左做匀速直线运动时,受到向左的拉力F、向右的摩擦力f和F动 ,
即;F=f+F动 ,
因f=F动 ,所以F=2f,即180N=2f,
解得:f=F动=90N,且此时摩擦力方向水平向右。
(2)动滑轮上有2段绳子承担拉力,滑轮与绳间摩擦、绳重和滑轮重均不计
那么动滑轮上受到的拉力和物体B的重力的关系为:F动=2GB;
则。
13.【答案】 (1)重力越大;动滑轮的重力;2和3;乙;80%
(2)减小接触面的粗糙程度(3)不能省功;B
【解答】(1)①比较实验1和2可知,在所有滑轮组一定时,提升的钩码重力越大,机械效率越高。
②比较实验3和4可知,二者动滑轮的重力不同,因此滑轮组的机械效率还与动滑轮的重力有关;
③探究滑轮组机械效率与提升钩码的高度无关是,必须控制其它因素相同而改变高度,故选2和3;
④在第5次实验中,钩码上升的高度h=0.2m,绳端移动的距离也是s=0.2m。根据s=nh可知,承担绳子的段数n=1,应该是乙图;
⑤利用图甲的装置,把重6N的物体用2.5N的拉力迅速拉起,
滑轮组的机械效率;
(2)小明利用图丙装置实验发现:斜面的机械效率与斜面的倾斜程度和摩擦有关,与物重无关。保持斜面倾斜程度不变,可以采用减小接触面的粗糙程度的方法减小摩擦,从而提高斜面的机械效率。
(3)验表明:额外功越小,总功越接近有用功;进一步推理得出:假设没有额外功,总功等于有用功;可见使用任何机械都不能省功。
这里使用的研究方法为实验+科学推理。
焦耳定律、阿基米德原理和欧姆定律,主要使用控制变量法,而只有牛顿第一定律使用实验+科学推理的方法,故选B。
14.【答案】 (1)解:物体A受到的浮力F浮为:F=ρgV=1.0×103kg/m3×10N/kg×100×10-3m3=1.0×103N
(2)解:拉力F移动的距离s=2h=2×2m=4m,
拉力F所做的总功W总=Fs=5000N×4m=2.0×104J,
则拉力F做功的功率:
(3)解:物体 A 的重力为G=mg=ρgV=9.0×103kg/m3×10N/kg×100×10-3m3=9.0×103N
滑轮组的机械效率为: =
【解析】(1)当物体完全浸没在水中时,它排开水的体积等于自身体积,此时根据阿基米德原理F浮=ρ液gV排计算它受到的浮力。
(2)首先根据s=nh计算出拉力移动的距离,再根据 W总=Fs 计算拉力所做的功,最后根据 计算出拉力的功率。
(3)首先根据G=mg=ρVg计算出物体A的重力,再根据 计算出滑轮组的机械效率。
15.【解答】解:(1)当泥土升高5m时,拉力F端距离15m,则n3,说明动滑轮有三段绳子承担,绳子的段数是奇数,则绳子从动滑轮开始绕起,如图所示:
(2)拉力F做的总功:
W总=Fs=400N×15m=6000J,
拉力F做的有用功:
W有=Gh=900N×5m=4500J,
滑轮组的机械效率:
η100%100%=75%;
(3)因为不计绳重及摩擦时F(G+G动),所以动滑轮的重力:
G动=nF﹣G=3×400N﹣900N=300N。
答:(1)如图所示;
(2)滑轮组的机械效率是75%;
(3)此时动滑轮的重量为300N。
3.4简单的机械(3)
A. W左图=W右图 ,η左图<η右图 B. W左图=W右图 ,η左图>η右图
C. W左图>W右图 ,η左图=η右图 D. W左图>W右图 ,η左图<η右图
2.如图所示,张伟回学利用斜面,用平行于斜面F=200N的推力,将质量为30kg的物体在5s时间内匀速推到1m高的平台上。斜面长s=2m,g取10N/kg,则( )
A.张伟所做的有用功为400J B.张伟所做的总功为700J
C.张伟的做功功率为140W D.斜面的机械效率为75%
3.小科用如图所示的滑轮组提升G为600N的重物,在绳子自由端施加F为250N的拉力,使重物在4s内匀速上升1m,不计绳重和摩擦。下列说法正确的是( )
A.动滑轮重100N B.拉力做功的功率为150W
C.绳子自由端移动的距离为2m D.此过程滑轮组的机械效率为80%
4.小明用图滑轮组将重为15N的物体匀速提升2m,手的拉力是6N.则( )
A.小明做的总功是30J
B.该滑轮组的机械效率是83.3%
C.若减小物重,可以增大机械效率
D.若加快提升速度,可以增大机械效率
5.如图所示,整个装置处于静止状态,弹簧测力计A、B、C的示数分别为FA、FB、FC , 以下有关弹簧测力计示数的关系,正确的是( )
A.FA=FB=FC B.FA=FB=3FC C.2FA=3FC=FB D.3FA=6FC=2FB
6.用如上图甲所示的滑轮组缓慢提升不同物体每次物体被提升的高度均为0.5m,滑轮组的机械效率与物体受到重力的关系如图乙所示,不计绳重和摩擦,下列分析正确的是( )
动滑轮的重力为5N
B.该滑轮组的机械效率可以达到100%
C.滑轮组的机械效率越高,拉力做功越少
D.每次提升重物时,滑轮组做的额外功为5J
7.为了将放置在水平地面上重为100N的物体提升一定高度,设置了如图所示的滑轮组装置。当用图乙所示随时间变化的竖直向下的拉力 F 拉绳时,物体的速度 V 和物体上升的高度 随时间变化的关系分别如图丙和丁所示。(不计绳重和绳与轮之间的摩擦)下列计算结果正确的是( )
A.0-1s内,地面对物体的支持力是10N
B.1-2s内,拉力 做的功是187.5J
C.2-3s内,拉力 的功率是100W
D.2-3s内,滑轮组的机械效率是62.5%
8.如图所示,质量为m的人站在质量为的均匀木板AB的中点,木板可以绕B端转动,2若以人的重力为动力,这属于 (选填“省力”或“费力”)杠杆。要使木板处于水平状态不动,此人拉力的大小为 。(摩擦忽略不计)
9.如图所示,用甲、乙两滑轮组匀速向上提升重物,物重都为600牛,不计动滑轮重及摩擦,绳子的拉力F甲为 牛;F乙为 牛。若将重物提高1米,则甲滑轮组绳子的自由端移动的距离为 米,乙滑轮组绳子的自由端移动的距离为 米。
10.如图甲所示,滑轮组在竖直向上的拉力F作用下,将重为105N的物体匀速提起,在5s时间内绳子自由端移动的距离为s=3m。图乙是滑轮组工作时的拉力F与绳自由端移动距离s的关系图。
(1)计算物体上升的速度。
(2)图乙中阴影部分的面积表示的物理量是 ,并列式计算出该物理量。
(3)计算滑轮组提升该重物时的机械效率。
11.工人利用斜面和滑轮将物体从斜面底端匀速拉到顶端,斜面高1m,长2m,物体重500N,平行于斜画的拉力200N,所用时间10s。在此过程中,物体动能 (选填“增大”、“减小”或“不变”)。重力势能 (选填“增大”、“减小”或“不变”)。拉力的功率为 W,把物体直接提高到斜面顶端做的功为有用功,则这个装置的机械效率为 。
12.如图所示,物体A在物体B的重力作用下做匀速直线运动。若在A上再施加一个水平向左、大小为180N的拉力F(图中未画出),则物体A向左做匀速直线运动,此时物体A与桌面之间的摩擦力为 N,方向 。物体B的重力是 。(不计绳重,轮重和摩擦)
13.在日常生活和工农业生产中,提高机械效率有着重要的意义。提高机械效率,要从研究影响机械效率的因素出发,寻求办法。
(1)为了探究影响机械效率的因素,小明选取了大小相同的滑轮,利用图甲和图乙装置进行实验,并把数据整理记录在下表中。
实验
次数 滑轮
材质 钩码重G/N 提升的高h/m 有用功
W有用/J 拉力F/N 绳端移动的距离S/m 总功
W总/J 机械效率/η
1 铝 1 0.1 0.1 0.6 0.3 0.18 56%
2 铝 2 0.1 0.2 1.0 0.3 0.3 67%
3 铝 2 0.2 0.4 1.0 0.6 0.6 67%
4 塑料 2 0.2 0.4 0.8 0.6 0.48 83%
5 塑料 2 0.2 0.4 2.1 0.2 0.42 95%
①比较1和2两次实验发现:在所有滑轮组一定时,提升的钩码________,机械效率越高。
②比较3和4两次实验发现:滑轮组的机械效率还与________有关。
③比较________两次实验发现:在所用滑轮组一定时,机械效率与提升钩码的高度无关。
④第5次实验是利用了图________的装置完成的。
⑤利用图甲的装置,把重6N的物体用2.5N的拉力迅速拉起,滑轮组的机械效率为________。可见如果没有刻度尺,只有测力计,也可以测量出滑轮组的机械效率。
(2)小明利用图丙装置实验发现:斜面的机械效率与斜面的倾斜程度和摩擦有关,与物重无关。保持斜面倾斜程度不变,可以采用________的方法减小摩擦,从而提高斜面的机械效率。
(3)实验表明:额外功越小,总功越接近有用功;进一步推理得出:假设没有额外功,总功等于有用功;可见使用任何机械都________。下列物理规律的得出运用了这种研究方法的是________。
A、焦耳定律 B、牛顿第一定律 C、阿基米德原理 D、欧姆定律
14.人们利用如图所示的滑轮组将浸没在河底的实心物体A打捞上来,物体A的密度为9.0×103kg/m3 , 体积为100dm3。在5000N的拉力F作用下,物体A在2s内匀速竖直上升2m(物体未露出水面),不计水的阻力,g取10N/kg,ρ水=1.0×103kg/m3。求:
(1).物体A受到的浮力。
(2).拉力F做功的功率。
(3).滑轮组的机械效率。
15.如图所示,是建筑工人从竖直深井中提取泥土时利用的滑轮组模型。如果某次操作中,工人用400N的拉力F在1分钟内将总重为900N的泥土匀速提升5m。在这段时间内拉力F移动的距离是15m。求:
(1)请根据情景在图中画出滑轮组的绕线方法。
(2)滑轮组的机械效率是多大?
(3)此时动滑轮的重量为多少N?(不考虑各种摩擦及绳重)
答案及解析
1.【答案】 A
【解答】木块的重力相等,斜面的高度相同,根据W有=Gh可知,木块克服重力做功相等,
即W左图=W右图。左图斜面的倾斜角度小于右图, 则木块对左边斜面的压力大于右图斜面,
那么左边斜面产生的摩擦力大于右图斜面;且左边斜面的长度大于右图斜面;
根据W额=fs可知,克服摩擦做的额外功W额左>W额右;
根据可知,左边的机械效率小于右边的机械效率; 即η左图<η右图。
2.【答案】D。
【解析】A、物体的重力:G=mg=30kg×10N/kg=300N,
张伟做的有用功:W有用=Gh=300N×1m=300J,故A错;
B、张伟做的总功:W总=Fs=200N×2m=400J,故B错;
C、张伟的做功功率:,故C错;
(4)斜面的机械效率:
3.【答案】D
【解析】A.根据公式得到:,解得:G动=150N,故A错误;
BC.拉力移动的距离s=nh=1m×3=3m,拉力的速度,拉力的功率P=Fv=250N×0.75m/s=187.5W,故B、C错误;
D.滑轮组的机械效率,故D正确。
4.【答案】B
【解析】A、由图可知n=3,拉力端移动的距离s=3h=3×2m=6m;
小明所做的总功:
W总=Fs=6N×6m=36J;故A错;
B、所做的有用功:W有用=Gh=15N×2m=30J;
滑轮组的机械效率:
C、若减小提升的物重,有用功减小、而额外功几乎不变,有用功与总功的比值减小,机械效率减小,故C错;
D、若加快提升速度,可以增大做功的功率,但有用功与总功的比值不变,不会增大机械效率,故D错。
5.【答案】 D
【解析】分别对左边的滑轮和右边的滑轮进行受力分析,根据二力平衡的知识计算出几个拉力之间的关系即可。
【解答】测力计C直接与绳子相连,则绳子上产生的拉力都是FC。
①以左边的滑轮为对象进行分析,它左边受到A测力计的拉力FA , 右边受到两根绳子的拉力,都是FC。根据二力平衡的知识得到:FA=2FC , 即3FA=6FC;
②以右边的滑轮为对象进行分析,它左边受到绳子的拉力三个,都是FC , 右边受到B测力计的拉力FB。根据二力平衡的知识得到:3FC=FB , 即6FC=2FB。
那么得到:3FA=6FC=2FB。
故选D。
6.【答案】D
【解析】(1)不计绳重和摩擦,根据滑轮组的机械效率,计算动滑轮的重力;
(2)使用滑轮组时,需要提升动滑轮做额外功,据此分析机械效率的数值范围;
(3)根据机械效率的定义分析判断;
(4)克服动滑轮的重力做额外功,即W额=G动h。
【解答】A.由图乙可知,提升物重G=10N时,滑轮组的机械效率η=50%,
不计绳重和摩擦,根据滑轮组的机械效率得到:;
解得:G动=10N,故A错误;
B.使用滑轮组时,需要提升动滑轮做额外功,使得有用功小于总功,滑轮组的机械效率总小于100%,故B错误;
C.滑轮组的机械效率越高,说明有用功与总功的比值越大,拉力做功不一定少,故C错误;
D.利用滑轮组每次物体被提升的高度均为0.5m,提升动滑轮上升的高度也都是0.5m,则每次提升重物时,滑轮组做的额外功都为:W额=G动h=10N×0.5m=5J,故D正确。
7.【答案】B
【解析】由滑轮组的结构可以看出,承担物重的绳子股数n=3,则拉力F移动的距离s=3h。
(1)将滑轮组和物体看做一个整体,根据二力平衡的知识列出平衡关系式,结合滑轮组的工作特点计算出地面对物体的支持力;
(2)根据图像确定2~3s内拉力F的数值和物体运动的速度,结合滑轮组的特点计算出自由端移动的速度,最后根据P=Fv计算出拉力做功的功率;
(3)使用滑轮组提升重物时,根据公式计算出机械效率;
(4)由F-t图象得出在1~2s内的拉力F,由h-t图象得出重物上升的高度,求出拉力F的作用点下降的距离,利用W=Fs求此时拉力做功。
根据图丙可知,0~1s内,物体运动的速度为0,即在地面上保持静止状态。
由图乙可知,在0~1s内,拉力F=30N.取动滑轮和重物为研究对象,受到向下的重力G和G动,向上的支持力F支,及三根绳子向上的拉力F′作用,根据二力平衡的知识得到,
地面对重物的支持力F支=G+G动-3F拉=100N+G动-3×30N=G动+10N,故A错误;
由图丙可知,在2~3s内,重物做匀速运动,此时的速度v3=2.50m/s,拉力F3=40N,
拉力F的作用点下降的速度v3′=3v3=3×2.50m/s=7.5m/s,
拉力做功功率P总=F3V3′=40N×7.5m/s=300W,故C错误;
滑轮组的机械效率:,故D错误;
在1~2s内,拉力F2=50N,重物上升高度h2=1.25m
拉力F的作用点下降的距离s2=3h2=3×1.25m=3.75m,
拉力做的功:W=F2S2=50N×3.75m=187.5J,故B正确。故选B。
8.【答案】 费力;
【解析】(1)比较动力臂和阻力臂的大小,从而确定杠杆的分类;
(2)根据杠杆的平衡条件F1L1=F2L2计算即可。
【解答】(1)根据图片可知,如果将人的重力看做动力,则动力臂为;绳子的拉力看做阻力,阻力臂为AB。此时动力臂小于阻力臂,为费力杠杆。
(2)根据图片可知,B点为支点,阻力为绳子上的拉力FA ,
而动力F1=G人+G木板-FA==mg-FA;
根据杠杆的平衡条件F1L1=F2L2得到:(mg-FA)×=FA×AB;
则此人的拉力FA=。
9.【答案】200;300;3;2
【解析】(1)根据甲图可知,承担重力的绳子段数n=3,则自由端的拉力。根据乙图可知,承担重力的绳子段数n=2,则自由端的拉力;
(2)甲滑轮组绳子自由端移动的距离s甲=n甲h=3×1m=3m;乙滑轮组绳子自由端移动的距离s乙=n乙h=2×1m=2m。
10.【答案】(1)物体上升的速度0.2m/s。
(2)图乙中阴影部分的面积表示的物理量是功,功的大小为150J。
(3)滑轮组提升该重物时的机械效率为70%。
【解析】(1)滑轮组由三段绳子承担总重,s=3h,,
物体上升的速度
纵坐标表示力的大小为50N,大小不变,横坐标表示距离,大小为3m,
所以阴影部分表示力所做的功W=Fs=50N×3m=150J;
(3)滑轮组的机械效率
11.【答案】不变;增大;80;62.5%。
【解析】(1)将物体从斜面底端匀速拉到顶端,质量不变,速度不变,则物体的动能不变。
(2)物体沿斜面升高,质量不变,高度变大,所以其重力势能增大。
(3)图中滑轮是动滑轮,则绳端通过的距离为:s=2L=2×2m=4m;
拉力做功为:W总=Fs=200N×4m=800J;
拉力的功率为:
(4)此过程的有用功为:W有=Gh=500N×1m=500J;
这个装置的机械效率为:62.5%
12.【答案】 90;水平向右;45N
【解析】(1)物体A在物体B的重力作用下向右做匀速直线运动,这时A受到的摩擦力等于动滑轮的拉力,即f=F动;当物体A向左做匀速直线运动时,分析A的受力情况,列出受力平衡式,进而求出A受到的摩擦力和动滑轮上受到的拉力F动。
(2)动滑轮上有2段绳子承担拉力,那么动滑轮上受到的拉力和物体B的重力的关系为:F动=2GB , 据此物体B的重力。
【解答】(1)物体A在物体B的重力作用下向右做匀速直线运动时,
则A受到的摩擦力等于动滑轮对A的拉力,即f=F动;
当物体A向左做匀速直线运动时,受到向左的拉力F、向右的摩擦力f和F动 ,
即;F=f+F动 ,
因f=F动 ,所以F=2f,即180N=2f,
解得:f=F动=90N,且此时摩擦力方向水平向右。
(2)动滑轮上有2段绳子承担拉力,滑轮与绳间摩擦、绳重和滑轮重均不计
那么动滑轮上受到的拉力和物体B的重力的关系为:F动=2GB;
则。
13.【答案】 (1)重力越大;动滑轮的重力;2和3;乙;80%
(2)减小接触面的粗糙程度(3)不能省功;B
【解答】(1)①比较实验1和2可知,在所有滑轮组一定时,提升的钩码重力越大,机械效率越高。
②比较实验3和4可知,二者动滑轮的重力不同,因此滑轮组的机械效率还与动滑轮的重力有关;
③探究滑轮组机械效率与提升钩码的高度无关是,必须控制其它因素相同而改变高度,故选2和3;
④在第5次实验中,钩码上升的高度h=0.2m,绳端移动的距离也是s=0.2m。根据s=nh可知,承担绳子的段数n=1,应该是乙图;
⑤利用图甲的装置,把重6N的物体用2.5N的拉力迅速拉起,
滑轮组的机械效率;
(2)小明利用图丙装置实验发现:斜面的机械效率与斜面的倾斜程度和摩擦有关,与物重无关。保持斜面倾斜程度不变,可以采用减小接触面的粗糙程度的方法减小摩擦,从而提高斜面的机械效率。
(3)验表明:额外功越小,总功越接近有用功;进一步推理得出:假设没有额外功,总功等于有用功;可见使用任何机械都不能省功。
这里使用的研究方法为实验+科学推理。
焦耳定律、阿基米德原理和欧姆定律,主要使用控制变量法,而只有牛顿第一定律使用实验+科学推理的方法,故选B。
14.【答案】 (1)解:物体A受到的浮力F浮为:F=ρgV=1.0×103kg/m3×10N/kg×100×10-3m3=1.0×103N
(2)解:拉力F移动的距离s=2h=2×2m=4m,
拉力F所做的总功W总=Fs=5000N×4m=2.0×104J,
则拉力F做功的功率:
(3)解:物体 A 的重力为G=mg=ρgV=9.0×103kg/m3×10N/kg×100×10-3m3=9.0×103N
滑轮组的机械效率为: =
【解析】(1)当物体完全浸没在水中时,它排开水的体积等于自身体积,此时根据阿基米德原理F浮=ρ液gV排计算它受到的浮力。
(2)首先根据s=nh计算出拉力移动的距离,再根据 W总=Fs 计算拉力所做的功,最后根据 计算出拉力的功率。
(3)首先根据G=mg=ρVg计算出物体A的重力,再根据 计算出滑轮组的机械效率。
15.【解答】解:(1)当泥土升高5m时,拉力F端距离15m,则n3,说明动滑轮有三段绳子承担,绳子的段数是奇数,则绳子从动滑轮开始绕起,如图所示:
(2)拉力F做的总功:
W总=Fs=400N×15m=6000J,
拉力F做的有用功:
W有=Gh=900N×5m=4500J,
滑轮组的机械效率:
η100%100%=75%;
(3)因为不计绳重及摩擦时F(G+G动),所以动滑轮的重力:
G动=nF﹣G=3×400N﹣900N=300N。
答:(1)如图所示;
(2)滑轮组的机械效率是75%;
(3)此时动滑轮的重量为300N。
3.4简单的机械(3)
同课章节目录
- 第1章 物质及其变化
- 第1节 物质的变化
- 第2节 物质的酸碱性
- 第3节 常见的酸
- 第4节 常见的碱
- 第5节 酸和碱之间发生的反应
- 第6节 几种重要的盐
- 第2章 物质转化与材料利用
- 第1节 金属材料
- 第2节 金属的化学性质
- 第3节 有机物和有机合成材料
- 第4节 物质的分类
- 第5节 物质的转化
- 第6节 材料的利用与发展
- 第3章 能量的转化与守恒
- 第1节 能量及其形式
- 第2节 机械能
- 第3节 能量转化的量度
- 第4节 简单机械
- 第5节 物体的内能
- 第6节 电能
- 第7节 核能
- 第8节 能量的转化与守恒
- 第4章 代谢与平衡
- 第1节 食物与营养
- 第2节 食物的消化与吸收
- 第3节 体内物质的运输
- 第4节 能量的获得
- 第5节 体内物质的动态平衡
- 研究性学习课题
- 一 当地酸雨情况以及对农作物和建筑物的影响
- 二 金属对社会发展的作用
- 三 寻找自行车中的杠杆
- 四 怎样防治龋齿
