沪科版数学七年级上册 4.3线段的长短比较(2)课件(共27张PPT)
文档属性
| 名称 | 沪科版数学七年级上册 4.3线段的长短比较(2)课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 417.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-09 00:00:00 | ||
图片预览




文档简介
(共27张PPT)
4.3 线段的长短比较(2)
(1)重(叠)合法—从“形”的角度比较
(2)度量法—从“数值”的角度比较
1.比较线段
长短的方法
2、用直尺和圆规作一条线段,使它等于已知线段、两条已知线段的和差。
3、若线段c的长度是线段a,b的长度的和(差),我们就说线段c是线段a,b的和(差)
4、要将一根小木条钉在墙壁上至少需要2个钉子,他的数学原理是:
知识回顾
5、如图,AB=CD,则AC与BD的大小关系是( )
A、AC>BD B、ACA
B
C
D
6、已知AB=6cm,AD=4cm,BC=5cm,则CD= 。
A
C
D
B
7、已知线段a,做线段AB,使得AB的长度等于2a
B
C
A
D
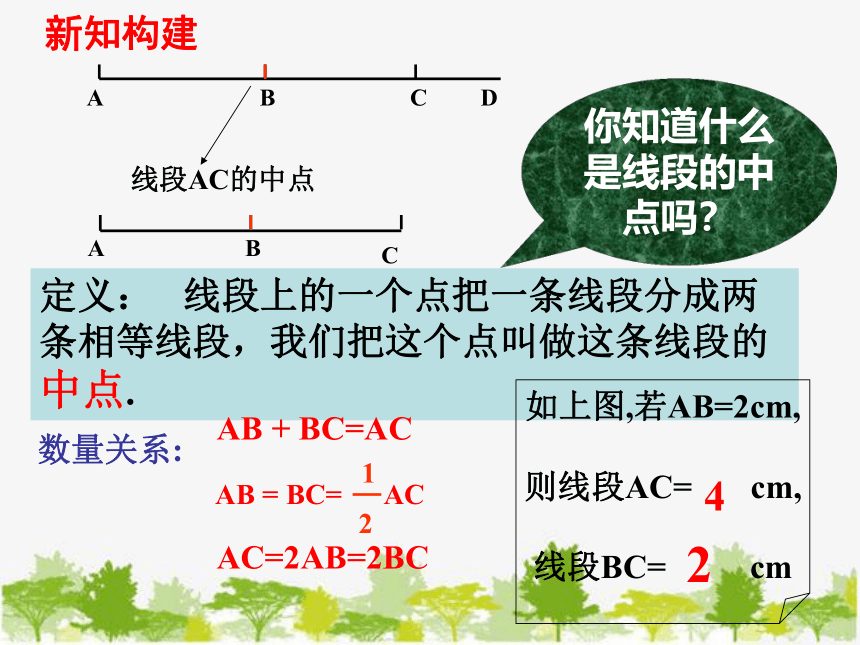
线段AC的中点
B
C
A
定义: 线段上的一个点把一条线段分成两条相等线段,我们把这个点叫做这条线段的中点.
数量关系:
AB + BC=AC
AB = BC= AC
1
2
你知道什么是线段的中点吗?
如上图,若AB=2cm,
则线段AC= cm,
线段BC= cm
4
2
AC=2AB=2BC
新知构建
随堂练习
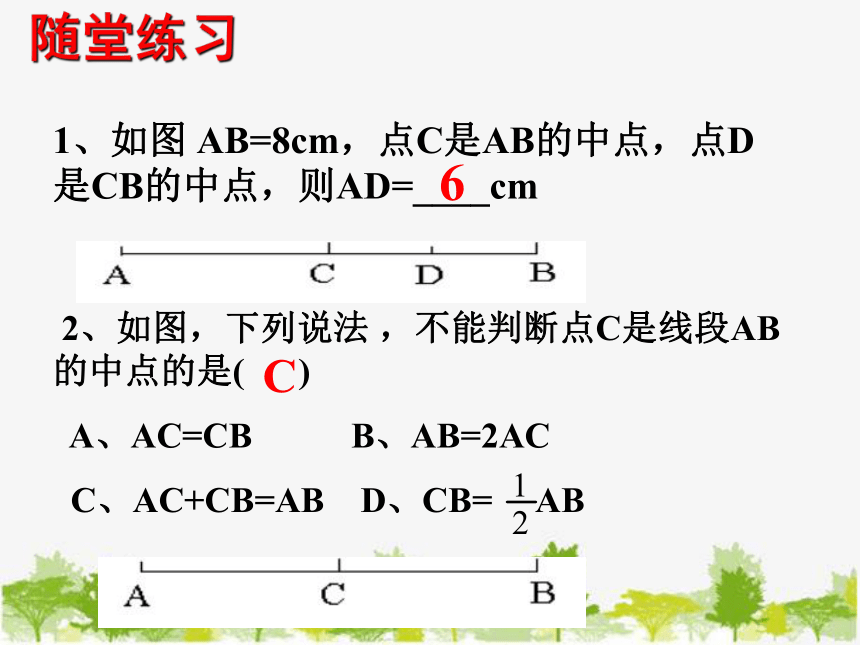
2、如图,下列说法 ,不能判断点C是线段AB的中点的是( )
A、AC=CB B、AB=2AC
C、AC+CB=AB D、CB= AB
C
1、如图 AB=8cm,点C是AB的中点,点D是CB的中点,则AD=____cm
6
B
A
D
C
6
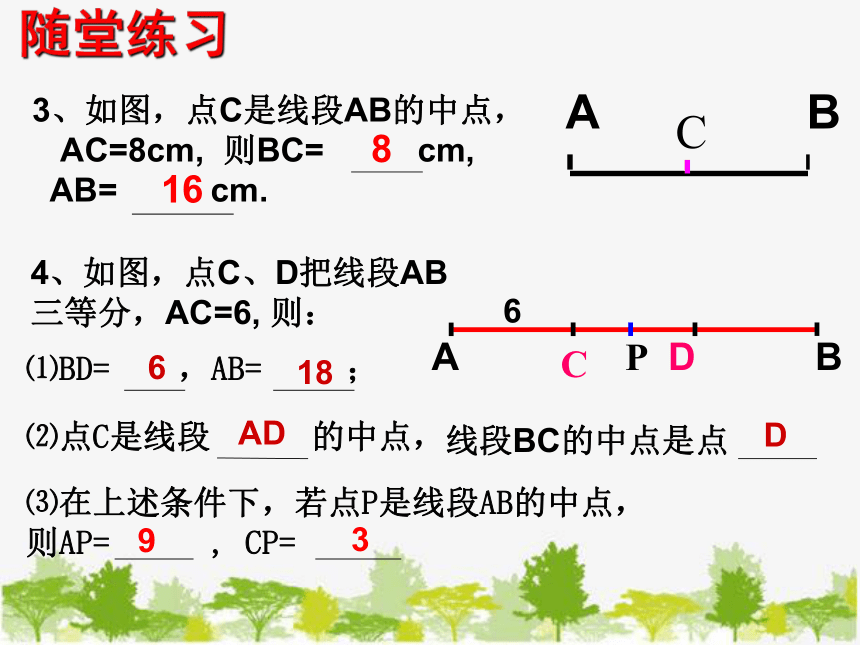
3、如图,点C是线段AB的中点,
AC=8cm, 则BC= cm,
AB= cm.
A
B
C
4、如图,点C、D把线段AB
三等分,AC=6, 则:
⑴BD= ,AB= ;
⑵点C是线段 的中点,
线段BC的中点是点 。
8
16
6
18
AD
D
⑶在上述条件下,若点P是线段AB的中点,
则AP= , CP=
P
9
3
随堂练习
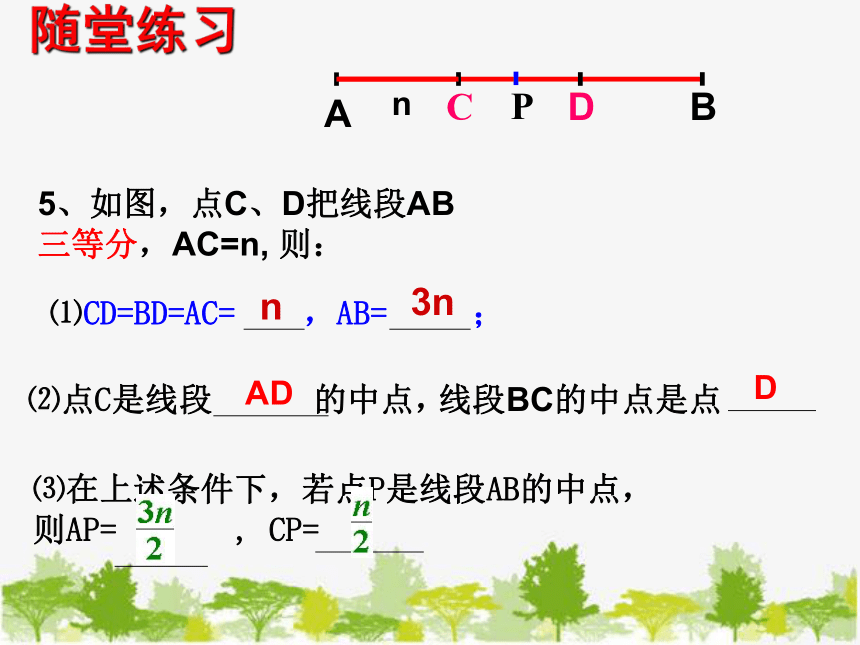
5、如图,点C、D把线段AB
三等分,AC=n, 则:
A
D
C
B
⑴CD=BD=AC= ,AB= ;
⑵点C是线段 的中点,
线段BC的中点是点 。
n
3n
AD
D
⑶在上述条件下,若点P是线段AB的中点,
则AP= , CP=
P
n
随堂练习
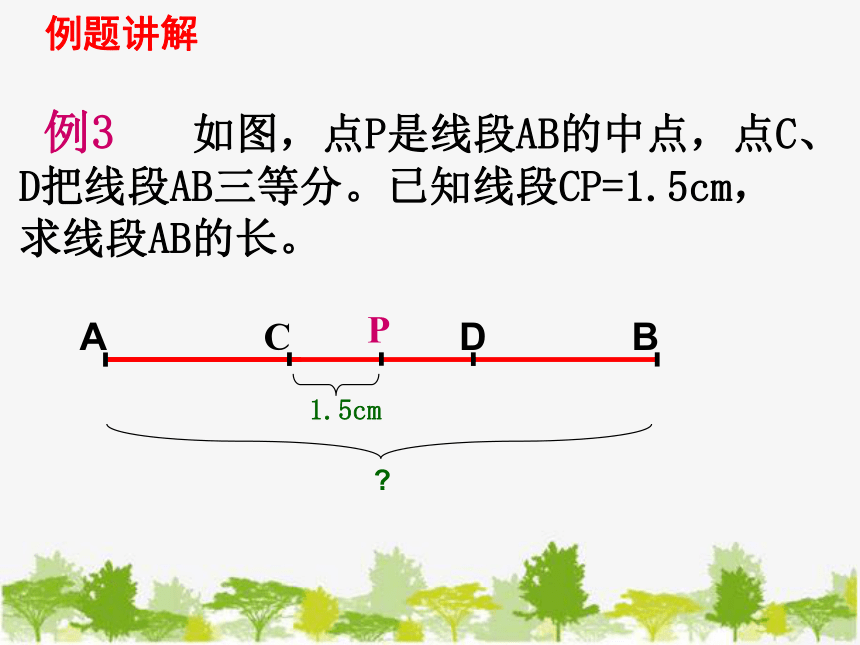
例3 如图,点P是线段AB的中点,点C、D把线段AB三等分。已知线段CP=1.5cm,
求线段AB的长。
B
A
D
C
P
1.5cm
例题讲解
∵ 点P是线段AB的中点,
∵ 点 C、D把线 段AB三等分,
∵ CP=AP -AC
即 AB的长是9cm
∴ AB=6PC
AB=6×1.5
解:
1.已知线段AB的长度为a, 延长线段AB至
点C(如图),使BC= , 问线段AC
的长为多少?
A
B
C
a
1.5a
随堂练习
A
B
C
O
2.已知B是线段AC上一点,AB=4cm,BC=3cm. 如果O是线段AC的中点, 求线段OB的长。
3.已知线段AB=6cm,延长线段AB至点C(如图),
使BC= AB,
问: ⑴线段AC的长为多少?
⑵若点D为线段AC的中点,
①求线段CD的长。
②求BD的长。
A
B
C
D
0.5cm
9cm
4.5cm
1.5cm
4. 在一条直线上顺次取A、B、C三点,使AB=5cm,
BC=2cm,并且取线段AC的中点O,求线段OB的长。
A
B
C
O
解:
AC=AB+BC=5+2=7cm
AO=OC= AC=3.5cm
1
2
OB=AB-AO=5-3.5=1.5cm
(或OB=OC-BC=3.5-2=1.5cm)
答:线段OB的长等于1.5cm.
如图,从小明家到学校共有三条路,小明为了尽快到学校,应选择第 条路。为什么?
学校
小明家
(1)
(2)
(3)
⑵
能否再建一条更短的路
新知构建
A
B
线段的性质:
实践出真知:
在所有连结两点的线中,线段最短。简单地说,两点之间线段最短。
大家看图,如果量一量车站与码头相距多远,是怎样量的?如果从你家到学校走了三公里,能否认为学校与你家的距离为3公里?
两点之间线段的长度, 叫做这两点之间的距离。
码头
车站
距离的含义是线段的长度。
下列说法正确的是( )
A.过A、B两点的直线长是A、B两点间的距离
B.线段AB就是A、B两点间的距离
C.乘火车从杭州到上海要走210千米,这就是说
杭州站与上海站间的距离为210千米
D. 连结A、B两点的所有线中,其中最短的线的长度
就是A、B两点间的距离
D
例题讲解
(1)如图:这是A、B两地之间的公路,在公路工
程改造计划时,为使A、B两地行程最短,应如何
设计线路?在图中画出。你的理由是
_______________________
两点之间线段最短
随堂练习
村庄A
村庄B
大桥P
河流
(2)如图,村庄A, B之间有一条河流,要在河流上建造一座大桥P, 为了使村庄A, B之间的距离最短,请问:这座大桥P应建造在哪里。为什么?请画出图形。
两点之间线段最短
(3)如图,A、B、C、D表示4个居民小区。现要建一个牛奶供应站,使它到4个小区的距离之和最小,你认为牛奶供应站应建在何处?标出牛奶供应站的位置,并说明理由。
A
C
B
D
P
∴点P就是所求的位置。
A
B
(4)在铁丝框的A处有一只蚂蚁,在B处有一粒蜜糖,蚂蚁想吃到蜜糖,所走的最短路程是多少cm?
4cm
A
B
4cm
A
B
4cm
A
B
C
其余条件不变,把B处的蜜糖改成C处,又该如何?
4cm
A
B
C
那将“立方体的铁丝框”改成“立方体的纸盒”,上述两题结论又该如何呢?
4cm
那将“立方体的铁丝框”改成“立方体的纸盒”,上述两题结论又该如何呢?
C”(C)
A
C
B
C’(C)
4cm
这节课你学会了什么?
1.线段的基本性质:两点之间线段最短。
2.两点之间的距离:两点之间线段的长度。
3.线段的中点的概念及表示方法。
课堂小结
4.3 线段的长短比较(2)
(1)重(叠)合法—从“形”的角度比较
(2)度量法—从“数值”的角度比较
1.比较线段
长短的方法
2、用直尺和圆规作一条线段,使它等于已知线段、两条已知线段的和差。
3、若线段c的长度是线段a,b的长度的和(差),我们就说线段c是线段a,b的和(差)
4、要将一根小木条钉在墙壁上至少需要2个钉子,他的数学原理是:
知识回顾
5、如图,AB=CD,则AC与BD的大小关系是( )
A、AC>BD B、AC
B
C
D
6、已知AB=6cm,AD=4cm,BC=5cm,则CD= 。
A
C
D
B
7、已知线段a,做线段AB,使得AB的长度等于2a
B
C
A
D
线段AC的中点
B
C
A
定义: 线段上的一个点把一条线段分成两条相等线段,我们把这个点叫做这条线段的中点.
数量关系:
AB + BC=AC
AB = BC= AC
1
2
你知道什么是线段的中点吗?
如上图,若AB=2cm,
则线段AC= cm,
线段BC= cm
4
2
AC=2AB=2BC
新知构建
随堂练习
2、如图,下列说法 ,不能判断点C是线段AB的中点的是( )
A、AC=CB B、AB=2AC
C、AC+CB=AB D、CB= AB
C
1、如图 AB=8cm,点C是AB的中点,点D是CB的中点,则AD=____cm
6
B
A
D
C
6
3、如图,点C是线段AB的中点,
AC=8cm, 则BC= cm,
AB= cm.
A
B
C
4、如图,点C、D把线段AB
三等分,AC=6, 则:
⑴BD= ,AB= ;
⑵点C是线段 的中点,
线段BC的中点是点 。
8
16
6
18
AD
D
⑶在上述条件下,若点P是线段AB的中点,
则AP= , CP=
P
9
3
随堂练习
5、如图,点C、D把线段AB
三等分,AC=n, 则:
A
D
C
B
⑴CD=BD=AC= ,AB= ;
⑵点C是线段 的中点,
线段BC的中点是点 。
n
3n
AD
D
⑶在上述条件下,若点P是线段AB的中点,
则AP= , CP=
P
n
随堂练习
例3 如图,点P是线段AB的中点,点C、D把线段AB三等分。已知线段CP=1.5cm,
求线段AB的长。
B
A
D
C
P
1.5cm
例题讲解
∵ 点P是线段AB的中点,
∵ 点 C、D把线 段AB三等分,
∵ CP=AP -AC
即 AB的长是9cm
∴ AB=6PC
AB=6×1.5
解:
1.已知线段AB的长度为a, 延长线段AB至
点C(如图),使BC= , 问线段AC
的长为多少?
A
B
C
a
1.5a
随堂练习
A
B
C
O
2.已知B是线段AC上一点,AB=4cm,BC=3cm. 如果O是线段AC的中点, 求线段OB的长。
3.已知线段AB=6cm,延长线段AB至点C(如图),
使BC= AB,
问: ⑴线段AC的长为多少?
⑵若点D为线段AC的中点,
①求线段CD的长。
②求BD的长。
A
B
C
D
0.5cm
9cm
4.5cm
1.5cm
4. 在一条直线上顺次取A、B、C三点,使AB=5cm,
BC=2cm,并且取线段AC的中点O,求线段OB的长。
A
B
C
O
解:
AC=AB+BC=5+2=7cm
AO=OC= AC=3.5cm
1
2
OB=AB-AO=5-3.5=1.5cm
(或OB=OC-BC=3.5-2=1.5cm)
答:线段OB的长等于1.5cm.
如图,从小明家到学校共有三条路,小明为了尽快到学校,应选择第 条路。为什么?
学校
小明家
(1)
(2)
(3)
⑵
能否再建一条更短的路
新知构建
A
B
线段的性质:
实践出真知:
在所有连结两点的线中,线段最短。简单地说,两点之间线段最短。
大家看图,如果量一量车站与码头相距多远,是怎样量的?如果从你家到学校走了三公里,能否认为学校与你家的距离为3公里?
两点之间线段的长度, 叫做这两点之间的距离。
码头
车站
距离的含义是线段的长度。
下列说法正确的是( )
A.过A、B两点的直线长是A、B两点间的距离
B.线段AB就是A、B两点间的距离
C.乘火车从杭州到上海要走210千米,这就是说
杭州站与上海站间的距离为210千米
D. 连结A、B两点的所有线中,其中最短的线的长度
就是A、B两点间的距离
D
例题讲解
(1)如图:这是A、B两地之间的公路,在公路工
程改造计划时,为使A、B两地行程最短,应如何
设计线路?在图中画出。你的理由是
_______________________
两点之间线段最短
随堂练习
村庄A
村庄B
大桥P
河流
(2)如图,村庄A, B之间有一条河流,要在河流上建造一座大桥P, 为了使村庄A, B之间的距离最短,请问:这座大桥P应建造在哪里。为什么?请画出图形。
两点之间线段最短
(3)如图,A、B、C、D表示4个居民小区。现要建一个牛奶供应站,使它到4个小区的距离之和最小,你认为牛奶供应站应建在何处?标出牛奶供应站的位置,并说明理由。
A
C
B
D
P
∴点P就是所求的位置。
A
B
(4)在铁丝框的A处有一只蚂蚁,在B处有一粒蜜糖,蚂蚁想吃到蜜糖,所走的最短路程是多少cm?
4cm
A
B
4cm
A
B
4cm
A
B
C
其余条件不变,把B处的蜜糖改成C处,又该如何?
4cm
A
B
C
那将“立方体的铁丝框”改成“立方体的纸盒”,上述两题结论又该如何呢?
4cm
那将“立方体的铁丝框”改成“立方体的纸盒”,上述两题结论又该如何呢?
C”(C)
A
C
B
C’(C)
4cm
这节课你学会了什么?
1.线段的基本性质:两点之间线段最短。
2.两点之间的距离:两点之间线段的长度。
3.线段的中点的概念及表示方法。
课堂小结
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
