2022-2023学年人教版数学八年级上册13.1.2 线段的垂直平分线的性质 课时练习 (word版含答案)
文档属性
| 名称 | 2022-2023学年人教版数学八年级上册13.1.2 线段的垂直平分线的性质 课时练习 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 184.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-09 11:56:03 | ||
图片预览



文档简介
2022-2023年人教版数学八年级上册13.1.2
《线段的垂直平分线的性质》课时练习
一 、选择题
1.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC,AC于点D和E,∠B=60°,∠C=25°,则∠BAD为( )
A.50° B.70° C.75° D.80°
2.到三角形三个顶点的距离都相等的点是这个三角形的( )
A.三条高的交点 B.三条角平分线的交点
C.三条中线的交点 D.三条边的垂直平分线的交点
3.如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是( )
A.10cm B.12cm C.15cm D.17cm
4.如图,MN是线段AB的垂直平分线,C在MN外,且与A点在MN的同一侧,BC交MN于P点,则( )
A.BC>PC+AP B.BC<PC+AP C.BC=PC+AP D.BC≥PC+AP
5.如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
6.数学活动课上,四位同学围绕作图问题:“如图,已知直线l和l外一点P,用直尺和圆规作直线PQ,使PQ⊥l于点Q.”分别作出了下列四个图形.其中作法错误的是( )
7.如图,A,B,C表示三个居民小区,为丰富居民们的文化生活,现准备建一个文化广场,使它到三个小区的距离相等,则文化广场应建在( )
A.AC,BC两边高线的交点处
B.AC,BC两边中线的交点处
C.AC,BC两边垂直平分线的交点处
D.∠A,∠B两内角平分线的交点处
8.在锐角△ABC内的一点P满足PA=PB=PC,则点P是△ABC( ).
A.三条角平分线的交点 B.三边垂直平分线的交点
C.三条高的交点 D.三条中线的交点
9.如图,将三角形纸片ABC沿直线DE折叠后,使得点B与点A重合,折痕分别交BC,AB于点D,E.如果AC=5cm,△ADC的周长为17cm,那么BC的长为( )
A.7cm B.10cm C.12cm D.22cm
10.如图,在△ABC中,AB=AC,D是BC的中点,AC的垂直平分线交AC,AD,AB于点E,O,F,则图中全等三角形的对数是( )
A.1对 B.2对 C.3对 D.4对
11.如图,已知线段AB,分别以点A、点B为圆心,以大于AB的长为半径画弧,两弧交于点C和点D,作直线CD,在CD上取两点F、E,连接FA、FB、EA、EB,则下列结论一定正确的是( )
A.PA=MA B.MA=PE C.PE=BE D.PA=PB
12.如图,在已知的△ABC中,按以下步骤作图:
①分别以B,C为圆心,以大于BC的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
A.90° B.95° C.100° D.105°
二 、填空题
13.如图,在△ABC中,AB=AC,∠A=50°,AB的垂直平分线分别交AC和AB于点D和E,那么∠DBC= .
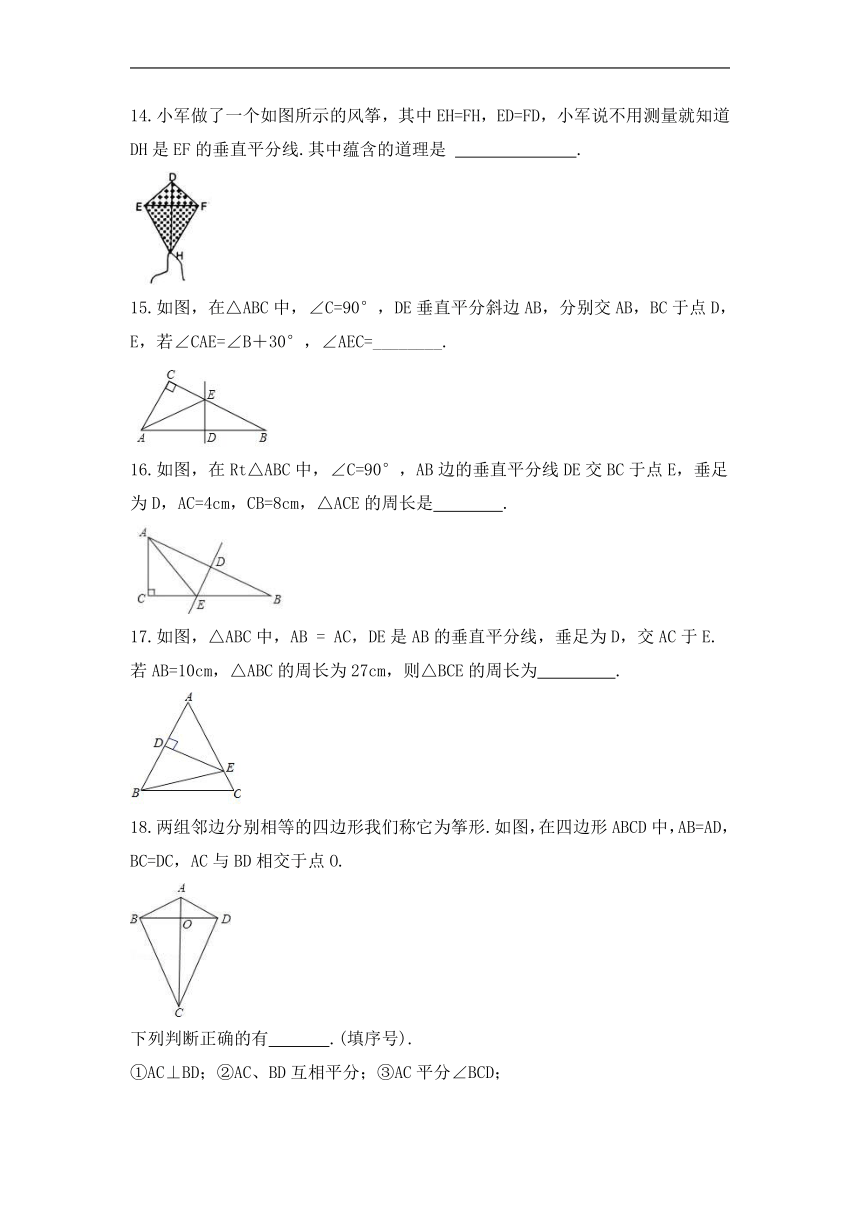
14.小军做了一个如图所示的风筝,其中EH=FH,ED=FD,小军说不用测量就知道DH是EF的垂直平分线.其中蕴含的道理是 .
15.如图,在△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB,BC于点D,E,若∠CAE=∠B+30°,∠AEC=________.
16.如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点E,垂足为D,AC=4cm,CB=8cm,△ACE的周长是 .
17.如图,△ABC中,AB = AC,DE是AB的垂直平分线,垂足为D,交AC于E.若AB=10cm,△ABC的周长为27cm,则△BCE的周长为 .
18.两组邻边分别相等的四边形我们称它为筝形.如图,在四边形ABCD中,AB=AD,BC=DC,AC与BD相交于点O.
下列判断正确的有 .(填序号).
① AC⊥BD;②AC、BD互相平分;③AC平分∠BCD;
④∠ABC=∠ADC=90°;⑤筝形ABCD的面积为AC×BD.
三 、作图题
19.某地有两所大学和两条相交叉的公路,如图、所示(点M,N表示大学,AO,BO表示公路).现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.
(1)你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案;
(2)阐述你设计的理由.
四 、解答题
20.如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
求证:直线AD是线段CE的垂直平分线.
21.如图,在△ABC中,∠BAC的平分线AD交BC于点D,DE垂直平分AC,垂足为点E,∠BAD=29°,求∠B的度数.
22.如图,在Rt△ABC中,∠ACB=90°
(1)用尺规作AB的垂直平分线MN交BC于点P(不写作法,保留作图痕迹).
(2)连接AP,如果AP平分∠CAB,求∠B的度数.
23.如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M.
(1)若∠B=70°,则∠NMA的度数是________.
(2)连接MB,若AB=8cm,△MBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在点P,使由P,B,C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.
参考答案
1.B.
2.D
3.C
4.C.
5.D.
6.A.
7.C
8.B.
9.C.
10.D.
11.D.
12.D
13.答案为:15°.
14.答案为:与线段两个端点距离相等的点在这条线段的垂直平分线线上.
15.答案为:40°
16.答案为:12cm.
17.答案为:17
18.答案为:①③⑤.
19.解:如图所示:
(1)连接MN,分别以M、N为圆心,以大于1/2AB为半径画圆,两圆相交于DE,连接DE,则DE即为线段MN的垂直平分线;
(2)以O为圆心,以任意长为半径画圆,分别交OA、OB于G、H,再分别以G、H为圆心,以大于1/2GH为半径画圆,两圆相交于F,连接OF,则OF即为∠AOB的平分线;
(3)DE与OF相交于点P,则点P即为所求。
20.证明:∵DE⊥AB,
∴∠AED=90°=∠ACB,
又∵AD平分∠BAC,
∴∠DAE=∠DAC,
∵AD=AD,
∴△AED≌△ACD,
∴AE=AC,
∵AD平分∠BAC,
∴AD⊥CE,
即直线AD是线段CE的垂直平分线.
21.解:∵AD平分∠BAC
∴∠BAD=∠DAE,
∵∠BAD=29°,
∴∠DAE=29°,
∴∠BAC=58°,
∵DE垂直平分AC,
∴AD=DC,
∴∠DAE=∠DCA=29°,
∵∠BAC+∠DCA+∠B=180°,
∴∠B=93°.
22.解:(1)如图,点P为所作;
(2)∵点P在AB的垂直平分线MN上
∴PA=PB,
∴∠B=∠PAB,
∵AP平分∠CAB,
∴∠PAB=∠CAB,
∴∠CAB=2∠B,
∵∠CAB+∠B=90°,
即2∠B+∠B=90°,
∴∠B=30°.
23.解:(1)50°
(2)猜想的结论为:∠NMA=2∠B﹣90°.
理由:∵AB=AC,
∴∠B=∠C,
∴∠A=180°﹣2∠B,
又∵MN垂直平分AB,
∴∠NMA=90°﹣∠A=90°﹣(180°﹣2∠B)=2∠B﹣90°.
如图:
①∵MN垂直平分AB.∴MB=MA,
又∵△MBC的周长是14cm,
∴AC+BC=14cm,∴BC=6cm.
②当点P与点M重合时,PB+CP的值最小,最小值是8cm.
《线段的垂直平分线的性质》课时练习
一 、选择题
1.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC,AC于点D和E,∠B=60°,∠C=25°,则∠BAD为( )
A.50° B.70° C.75° D.80°
2.到三角形三个顶点的距离都相等的点是这个三角形的( )
A.三条高的交点 B.三条角平分线的交点
C.三条中线的交点 D.三条边的垂直平分线的交点
3.如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是( )
A.10cm B.12cm C.15cm D.17cm
4.如图,MN是线段AB的垂直平分线,C在MN外,且与A点在MN的同一侧,BC交MN于P点,则( )
A.BC>PC+AP B.BC<PC+AP C.BC=PC+AP D.BC≥PC+AP
5.如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
6.数学活动课上,四位同学围绕作图问题:“如图,已知直线l和l外一点P,用直尺和圆规作直线PQ,使PQ⊥l于点Q.”分别作出了下列四个图形.其中作法错误的是( )
7.如图,A,B,C表示三个居民小区,为丰富居民们的文化生活,现准备建一个文化广场,使它到三个小区的距离相等,则文化广场应建在( )
A.AC,BC两边高线的交点处
B.AC,BC两边中线的交点处
C.AC,BC两边垂直平分线的交点处
D.∠A,∠B两内角平分线的交点处
8.在锐角△ABC内的一点P满足PA=PB=PC,则点P是△ABC( ).
A.三条角平分线的交点 B.三边垂直平分线的交点
C.三条高的交点 D.三条中线的交点
9.如图,将三角形纸片ABC沿直线DE折叠后,使得点B与点A重合,折痕分别交BC,AB于点D,E.如果AC=5cm,△ADC的周长为17cm,那么BC的长为( )
A.7cm B.10cm C.12cm D.22cm
10.如图,在△ABC中,AB=AC,D是BC的中点,AC的垂直平分线交AC,AD,AB于点E,O,F,则图中全等三角形的对数是( )
A.1对 B.2对 C.3对 D.4对
11.如图,已知线段AB,分别以点A、点B为圆心,以大于AB的长为半径画弧,两弧交于点C和点D,作直线CD,在CD上取两点F、E,连接FA、FB、EA、EB,则下列结论一定正确的是( )
A.PA=MA B.MA=PE C.PE=BE D.PA=PB
12.如图,在已知的△ABC中,按以下步骤作图:
①分别以B,C为圆心,以大于BC的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
A.90° B.95° C.100° D.105°
二 、填空题
13.如图,在△ABC中,AB=AC,∠A=50°,AB的垂直平分线分别交AC和AB于点D和E,那么∠DBC= .
14.小军做了一个如图所示的风筝,其中EH=FH,ED=FD,小军说不用测量就知道DH是EF的垂直平分线.其中蕴含的道理是 .
15.如图,在△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB,BC于点D,E,若∠CAE=∠B+30°,∠AEC=________.
16.如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点E,垂足为D,AC=4cm,CB=8cm,△ACE的周长是 .
17.如图,△ABC中,AB = AC,DE是AB的垂直平分线,垂足为D,交AC于E.若AB=10cm,△ABC的周长为27cm,则△BCE的周长为 .
18.两组邻边分别相等的四边形我们称它为筝形.如图,在四边形ABCD中,AB=AD,BC=DC,AC与BD相交于点O.
下列判断正确的有 .(填序号).
① AC⊥BD;②AC、BD互相平分;③AC平分∠BCD;
④∠ABC=∠ADC=90°;⑤筝形ABCD的面积为AC×BD.
三 、作图题
19.某地有两所大学和两条相交叉的公路,如图、所示(点M,N表示大学,AO,BO表示公路).现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.
(1)你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案;
(2)阐述你设计的理由.
四 、解答题
20.如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
求证:直线AD是线段CE的垂直平分线.
21.如图,在△ABC中,∠BAC的平分线AD交BC于点D,DE垂直平分AC,垂足为点E,∠BAD=29°,求∠B的度数.
22.如图,在Rt△ABC中,∠ACB=90°
(1)用尺规作AB的垂直平分线MN交BC于点P(不写作法,保留作图痕迹).
(2)连接AP,如果AP平分∠CAB,求∠B的度数.
23.如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M.
(1)若∠B=70°,则∠NMA的度数是________.
(2)连接MB,若AB=8cm,△MBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在点P,使由P,B,C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.
参考答案
1.B.
2.D
3.C
4.C.
5.D.
6.A.
7.C
8.B.
9.C.
10.D.
11.D.
12.D
13.答案为:15°.
14.答案为:与线段两个端点距离相等的点在这条线段的垂直平分线线上.
15.答案为:40°
16.答案为:12cm.
17.答案为:17
18.答案为:①③⑤.
19.解:如图所示:
(1)连接MN,分别以M、N为圆心,以大于1/2AB为半径画圆,两圆相交于DE,连接DE,则DE即为线段MN的垂直平分线;
(2)以O为圆心,以任意长为半径画圆,分别交OA、OB于G、H,再分别以G、H为圆心,以大于1/2GH为半径画圆,两圆相交于F,连接OF,则OF即为∠AOB的平分线;
(3)DE与OF相交于点P,则点P即为所求。
20.证明:∵DE⊥AB,
∴∠AED=90°=∠ACB,
又∵AD平分∠BAC,
∴∠DAE=∠DAC,
∵AD=AD,
∴△AED≌△ACD,
∴AE=AC,
∵AD平分∠BAC,
∴AD⊥CE,
即直线AD是线段CE的垂直平分线.
21.解:∵AD平分∠BAC
∴∠BAD=∠DAE,
∵∠BAD=29°,
∴∠DAE=29°,
∴∠BAC=58°,
∵DE垂直平分AC,
∴AD=DC,
∴∠DAE=∠DCA=29°,
∵∠BAC+∠DCA+∠B=180°,
∴∠B=93°.
22.解:(1)如图,点P为所作;
(2)∵点P在AB的垂直平分线MN上
∴PA=PB,
∴∠B=∠PAB,
∵AP平分∠CAB,
∴∠PAB=∠CAB,
∴∠CAB=2∠B,
∵∠CAB+∠B=90°,
即2∠B+∠B=90°,
∴∠B=30°.
23.解:(1)50°
(2)猜想的结论为:∠NMA=2∠B﹣90°.
理由:∵AB=AC,
∴∠B=∠C,
∴∠A=180°﹣2∠B,
又∵MN垂直平分AB,
∴∠NMA=90°﹣∠A=90°﹣(180°﹣2∠B)=2∠B﹣90°.
如图:
①∵MN垂直平分AB.∴MB=MA,
又∵△MBC的周长是14cm,
∴AC+BC=14cm,∴BC=6cm.
②当点P与点M重合时,PB+CP的值最小,最小值是8cm.
