2022-2023学年鲁教版(五四学制)七年级数学上册第1章三角形 单元练习题(word版含答案)
文档属性
| 名称 | 2022-2023学年鲁教版(五四学制)七年级数学上册第1章三角形 单元练习题(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 271.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-09 17:57:04 | ||
图片预览




文档简介
2022-2023学年鲁教版(五四学制)七年级数学上册《第1章三角形》同步练习题(附答案)
一.选择题
1.已知三角形的三边长分别是3,8,x;若x的值为偶数,则x的值有( )
A.6个 B.5个 C.4个 D.3个
2.王老师的一块三角形教学用玻璃不小心打破了(如图),他想再到玻璃店划一块,为了方便他只要带哪一块就可以了( )
A.① B.② C.③ D.④
3.下列说法中:①三角形的角平分线、中线、高线都是线段;②直角三角形只有一条高线;③三角形的中线可能在三角形的外部;④三角形的高线可能在三角形的内部,也可能在三角形的外部,其中说法正确的有( )个.
A.1 B.2 C.3 D.4
4.以圆周上6点中的任意3点为顶点连三角形,一共可以连成多少个不同的三角形( )
A.216 B.120 C.40 D.20
5.如图所示,已知直线AB∥CD,∠C=125°,∠A=45°,则∠E的度数为( )
A.70° B.80° C.90° D.100°
6.三角形三条中线的交点叫做三角形的( )
A.内心 B.外心 C.中心 D.重心
7.如图,已知AB=DC,需添加下列( )条件后,就一定能判定△ABC≌△DCB.
A.AO=BO B.∠ACB=∠DBC C.AC=DB D.BO=CO
8.如图,点D为边BC的中点,AE为△ABD的中线,设△ABC的面积为S,△ABE的面积为S1,则下列结论正确的是( )
A.S=3S1 B.S=4S1 C.S=5S1 D.S=6S1
9.如图,点D在AB上,点E在AC上,AB=AC.下列条件中不能判断△ABE≌△ACD的是( )
A.BD=CE B.BE=CD C.AD=AE D.∠B=∠C
10.直角三角形的两个锐角( )
A.互补 B.相等 C.不等 D.互余
11.下列长度的三条线段,能组成三角形的是( )
A.2,3,4 B.3,4,8 C.4,4,8 D.5,5,11
12.关于三角形的三条高,下列说法正确的是( )
A.三条高都在三角形的内部 B.三条高都在三角形的外部
C.至多有一条在三角形的内部 D.至少有一条在三角形的内部
13.如图,在△ABC中,∠A=50°,∠C=72°,BD是△ABC的一条角平分线,则∠ABD的度数为( )
A.29° B.58° C.36° D.25°
14.在下列每组图形中,是全等形的是( )
A. B.
C. D.
15.伸缩门可自由伸缩,开关方便,随处可见,它凸显了四边形的( )
A.稳定性 B.不稳定性 C.对称性 D.美观性
二.填空题
16.如图,要测量河两岸相对两点A、B间的距离,先在过点B的AB的垂线上取两点C、D,使CD=BC,再在过点D的垂线上取点E,使A、C、E三点在一条直线上,可证明△EDC≌△ABC,所以测得ED的长就是A、B两点间的距离,这里判定△EDC≌△ABC的理由是 .
17.如图,在新修的小区中,有一条“Z”字形绿色长廊ABCD,其中AB∥CD,在AB,BC,CD三段绿色长廊上各修一小亭E,M,F,且BE=CF,点M是BC的中点,在凉亭M与F之间有一池塘,不能直接到达,要想知道M与F的距离,只需要测出线段 的长度.理由是依据 可以证明 ,从而由全等三角形对应边相等得出.
18.如图,在△ABD和△CDB中,AD=CB,AB、CD相交于点O,请你补充一个条件,使得△ABD≌△CDB.你补充的条件是 .
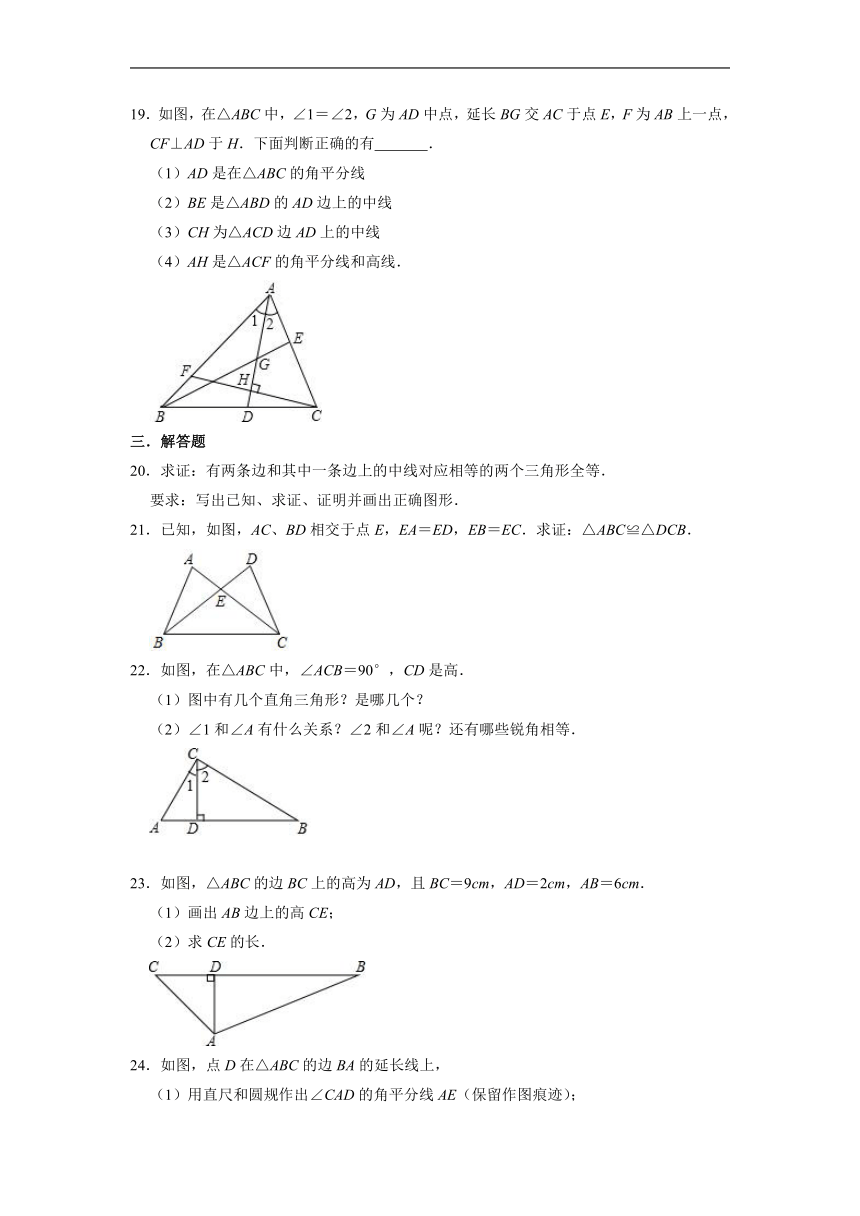
19.如图,在△ABC中,∠1=∠2,G为AD中点,延长BG交AC于点E,F为AB上一点,CF⊥AD于H.下面判断正确的有 .
(1)AD是在△ABC的角平分线
(2)BE是△ABD的AD边上的中线
(3)CH为△ACD边AD上的中线
(4)AH是△ACF的角平分线和高线.
三.解答题
20.求证:有两条边和其中一条边上的中线对应相等的两个三角形全等.
要求:写出已知、求证、证明并画出正确图形.
21.已知,如图,AC、BD相交于点E,EA=ED,EB=EC.求证:△ABC≌△DCB.
22.如图,在△ABC中,∠ACB=90°,CD是高.
(1)图中有几个直角三角形?是哪几个?
(2)∠1和∠A有什么关系?∠2和∠A呢?还有哪些锐角相等.
23.如图,△ABC的边BC上的高为AD,且BC=9cm,AD=2cm,AB=6cm.
(1)画出AB边上的高CE;
(2)求CE的长.
24.如图,点D在△ABC的边BA的延长线上,
(1)用直尺和圆规作出∠CAD的角平分线AE(保留作图痕迹);
(2)若∠B=∠C,求证:AE∥BC.
25.如图,在等腰△ABC中,AB=AC,△ADE是等边三角形,且DE∥BC,AD,AE分别交BC于点M,N.求证:BM=CN.
参考答案
一.选择题
1.解:根据题意得:5<x<11.
∵x是偶数,
∴可以取6,8,10这三个数.
故选:D.
2.解:②块,因为它只是其中不规则的一块,如果仅凭这一块不能配到与原来一样大小的三角形玻璃;
③、④块,它只保留了原来的一个角,那么这样去配也有很大的难度;
①块,因为它不但有两个角还有一个边,这正好符合全等三角形的判定中的ASA.
所以应该带第①块去.
故选:A.
3.解:①三角形的角平分线、中线、高都是线段,故本小题正确;
②直角三角形有三条高,故本小题错误;
③三角形的中线一定在三角形的内部,一定不在三角形外部,故本小题错误;
④锐角三角形的高都在三角形内部,钝角三角形有两条在三角形的外部,故本小题正确.
说法正确的有2个.
故选:B.
4.解:根据题意得:C63=20.
故选:D.
5.解:∵AB∥CD,∠C=125°,∴∠BFE=125°.∴∠E=∠BFE﹣∠A=125°﹣45°=80°.
故选:B.
6.解:三角形的重心是三角形三条中线的交点.
故选:D.
7.解:A、添加AO=BO不能判定△ABC≌△DCB,故此选项不合题意;
B、添加∠ACB=∠DBC不能判定△ABC≌△DCB,故此选项不合题意;
C、添加AC=DB可利用SSS判定△ABC≌△DCB,故此选项符合题意;
D、添加BO=CO不能判定△ABC≌△DCB,故此选项不合题意;
故选:C.
8.解:作AF⊥BC.
∵S△ADB=BD×AF×=,
S△ADC=CD×AF×=S,
又∵AD为△ABC中BC边上的中线,
∴BD=CD,
∴S△ADB=S△ADC,
同理,
∴S△ABE=S△ABC,
即S1=S,
∴S=4S1,
故选:B.
9.解:若BD=CE,则依据AB=AC,可得AD=AE,
由AB=AC,∠A=∠A,AE=AD,可得△ABE≌△ACD(SAS),
故A选项能判断△ABE≌△ACD;
若BE=CD,则不能得到△ABE≌△ACD,
故B选项不能判断△ABE≌△ACD;
若AD=AE,则可得△ABE≌△ACD(SAS),
故C选项能判断△ABE≌△ACD;
若∠B=∠C,则由∠B=∠C,AB=AC,∠A=∠A,可得△ABE≌△ACD(ASA),
故D选项能判断△ABE≌△ACD;
故选:B.
10.解:∵∠A+∠B+∠C=180°,∠C=90°,
∴∠A+∠B=180°﹣∠C=90°,
∴∠A和∠B互余.
故选:D.
11.解:A.∵2+3>4,∴能构成三角形;
B.∵3+4<8,∴不能构成三角形;
C.∵4+4=8,∴不能构成三角形;
D.∵5+5<11,∴不能构成三角形.
故选:A.
12.解:锐角三角形有三条高,高都在三角形内部;
直角三角形有两条高即三角形的两条直角边,一条在内部;
钝角三角形有三条高,一条高在三角形内部,另外两条高在三角形外部,
所以A、B、C都错误,
只有D是正确的.
故选:D.
13.解:∵在△ABC中,∠A=50°,∠C=72°,
∴∠ABC=180°﹣50°﹣72°=58°,
∵BD是△ABC的一条角平分线,
∴∠ABD=29°,
故选:A.
14.解:A、不是全等形,故此选项错误;
B、不是全等形,故此选项错误;
C、是全等形,故此选项正确;
D、不是全等形,故此选项错误;
故选:C.
15.解:伸缩门可自由伸缩,开关方便,随处可见,它凸显了四边形的不稳定性.
故选:B.
二.填空题
16.解:∵AB⊥BD,ED⊥BD,
∴∠ABD=∠EDC=90°,
在△EDC和△ABC中,
,
∴△EDC≌△ABC(ASA).
故答案为:ASA.
17.解:要想知道M与F的距离,只需要测出线段EM的长度.
理由是依据SAS可以证明△BEM≌△CFM,从而由全等三角形对应边相等得出.
证明:连接EF
∵AB∥CD,(已知)
∴∠B=∠C(两线平行内错角相等).
∵M是BC中点
∴BM=CM,
∵在△BEM和△CFM中,
∴△BEM≌△CFM(SAS).
∴CF=BE(对应边相等).
故答案为:EM,SAS,△BEM≌△CFM.
18.解:补充的条件是AB=CD,
理由是:在△ABD和△CDB中,
,
∴△ABD≌△CDB(SSS),
故答案为:AB=CD(答案不唯一).
19.解:(1)根据三角形的角平分线的概念,知AD是△ABC的角平分线,故此说法正确;
(2)根据三角形的中线的概念,知BG是△ABD的边AD上的中线,故此说法不正确;
(3)根据三角形的高的概念,知CH为△ACD的边AD上的高,故此说法不正确;
(4)根据三角形的角平分线和高的概念,知AH是△ACF的角平分线和高线,故此说法正确.
故答案为(1)(4).
三.解答题
20.已知:AD和A′D′分别为△ABC和△A′B′C′中线,且AD=A′D′,AB=A′B′,BC=B′C′,如图,
求证:△ABC≌△A′B′C′.
证明:∵AD和A′D′分别为△ABC和△A′B′C′中线,
∴BD=BC,B′D′=B′C′,
而BC=B′C′,
∴BD=B′D′,
在△ABD和△A′B′D′中
,
∴△ABD≌△A′B′D′(SSS),
∴∠B=∠B′,
在△ABC和△A′B′C′中
,
∴△ABC≌△A′B′C′(SAS),
即有两条边和其中一条边上的中线对应相等的两个三角形全等.
21.证明:在△AEB和△DEC中
,
∴△AEB≌△DEC(SAS),
∴∠BAE=∠CDE,AB=CD,
∵EA=ED,EB=EC,
∴AC=BD,
在△ABC和△DCB中
∴△ABC≌△DCB(SAS).
22.解:(1)∠ACB=90°,∠ADC=90°,
∴图中有3个直角三角形,分别是△ACD,△BCD,△ABC.
(2)∵∠ADC=90°,
∴∠1+∠A=90°,
∵∠1+∠2=90°,
∴∠2=∠A,∠1=∠B.
23.解:(1)如图所示:
(2) BC AD= AB CE,
×9×2=×6 CE,
解得:CE=3.
24.解:(1)如图所示,AE即为所求:
(2)∵AE平分∠CAD,
∴∠DAE=∠EAC,
∵∠B=∠C,∠DAC=∠B+∠C,
∴∠DAE=∠B=∠C=∠EAC,
∴AE∥BC.
25.解:∵△ADE是等边三角形,
∴∠D=∠E=60°,
∵DE∥BC,
∴∠AMN=∠D,∠ANM=∠E,
∴∠AMN=∠ANM=60°,
∴∠AMB=∠ANC=120°,
∵AB=AC,
∴∠B=∠C,
在△ABM和△ACN中,
∴△ABM≌△ACN,
∴BM=CN.
一.选择题
1.已知三角形的三边长分别是3,8,x;若x的值为偶数,则x的值有( )
A.6个 B.5个 C.4个 D.3个
2.王老师的一块三角形教学用玻璃不小心打破了(如图),他想再到玻璃店划一块,为了方便他只要带哪一块就可以了( )
A.① B.② C.③ D.④
3.下列说法中:①三角形的角平分线、中线、高线都是线段;②直角三角形只有一条高线;③三角形的中线可能在三角形的外部;④三角形的高线可能在三角形的内部,也可能在三角形的外部,其中说法正确的有( )个.
A.1 B.2 C.3 D.4
4.以圆周上6点中的任意3点为顶点连三角形,一共可以连成多少个不同的三角形( )
A.216 B.120 C.40 D.20
5.如图所示,已知直线AB∥CD,∠C=125°,∠A=45°,则∠E的度数为( )
A.70° B.80° C.90° D.100°
6.三角形三条中线的交点叫做三角形的( )
A.内心 B.外心 C.中心 D.重心
7.如图,已知AB=DC,需添加下列( )条件后,就一定能判定△ABC≌△DCB.
A.AO=BO B.∠ACB=∠DBC C.AC=DB D.BO=CO
8.如图,点D为边BC的中点,AE为△ABD的中线,设△ABC的面积为S,△ABE的面积为S1,则下列结论正确的是( )
A.S=3S1 B.S=4S1 C.S=5S1 D.S=6S1
9.如图,点D在AB上,点E在AC上,AB=AC.下列条件中不能判断△ABE≌△ACD的是( )
A.BD=CE B.BE=CD C.AD=AE D.∠B=∠C
10.直角三角形的两个锐角( )
A.互补 B.相等 C.不等 D.互余
11.下列长度的三条线段,能组成三角形的是( )
A.2,3,4 B.3,4,8 C.4,4,8 D.5,5,11
12.关于三角形的三条高,下列说法正确的是( )
A.三条高都在三角形的内部 B.三条高都在三角形的外部
C.至多有一条在三角形的内部 D.至少有一条在三角形的内部
13.如图,在△ABC中,∠A=50°,∠C=72°,BD是△ABC的一条角平分线,则∠ABD的度数为( )
A.29° B.58° C.36° D.25°
14.在下列每组图形中,是全等形的是( )
A. B.
C. D.
15.伸缩门可自由伸缩,开关方便,随处可见,它凸显了四边形的( )
A.稳定性 B.不稳定性 C.对称性 D.美观性
二.填空题
16.如图,要测量河两岸相对两点A、B间的距离,先在过点B的AB的垂线上取两点C、D,使CD=BC,再在过点D的垂线上取点E,使A、C、E三点在一条直线上,可证明△EDC≌△ABC,所以测得ED的长就是A、B两点间的距离,这里判定△EDC≌△ABC的理由是 .
17.如图,在新修的小区中,有一条“Z”字形绿色长廊ABCD,其中AB∥CD,在AB,BC,CD三段绿色长廊上各修一小亭E,M,F,且BE=CF,点M是BC的中点,在凉亭M与F之间有一池塘,不能直接到达,要想知道M与F的距离,只需要测出线段 的长度.理由是依据 可以证明 ,从而由全等三角形对应边相等得出.
18.如图,在△ABD和△CDB中,AD=CB,AB、CD相交于点O,请你补充一个条件,使得△ABD≌△CDB.你补充的条件是 .
19.如图,在△ABC中,∠1=∠2,G为AD中点,延长BG交AC于点E,F为AB上一点,CF⊥AD于H.下面判断正确的有 .
(1)AD是在△ABC的角平分线
(2)BE是△ABD的AD边上的中线
(3)CH为△ACD边AD上的中线
(4)AH是△ACF的角平分线和高线.
三.解答题
20.求证:有两条边和其中一条边上的中线对应相等的两个三角形全等.
要求:写出已知、求证、证明并画出正确图形.
21.已知,如图,AC、BD相交于点E,EA=ED,EB=EC.求证:△ABC≌△DCB.
22.如图,在△ABC中,∠ACB=90°,CD是高.
(1)图中有几个直角三角形?是哪几个?
(2)∠1和∠A有什么关系?∠2和∠A呢?还有哪些锐角相等.
23.如图,△ABC的边BC上的高为AD,且BC=9cm,AD=2cm,AB=6cm.
(1)画出AB边上的高CE;
(2)求CE的长.
24.如图,点D在△ABC的边BA的延长线上,
(1)用直尺和圆规作出∠CAD的角平分线AE(保留作图痕迹);
(2)若∠B=∠C,求证:AE∥BC.
25.如图,在等腰△ABC中,AB=AC,△ADE是等边三角形,且DE∥BC,AD,AE分别交BC于点M,N.求证:BM=CN.
参考答案
一.选择题
1.解:根据题意得:5<x<11.
∵x是偶数,
∴可以取6,8,10这三个数.
故选:D.
2.解:②块,因为它只是其中不规则的一块,如果仅凭这一块不能配到与原来一样大小的三角形玻璃;
③、④块,它只保留了原来的一个角,那么这样去配也有很大的难度;
①块,因为它不但有两个角还有一个边,这正好符合全等三角形的判定中的ASA.
所以应该带第①块去.
故选:A.
3.解:①三角形的角平分线、中线、高都是线段,故本小题正确;
②直角三角形有三条高,故本小题错误;
③三角形的中线一定在三角形的内部,一定不在三角形外部,故本小题错误;
④锐角三角形的高都在三角形内部,钝角三角形有两条在三角形的外部,故本小题正确.
说法正确的有2个.
故选:B.
4.解:根据题意得:C63=20.
故选:D.
5.解:∵AB∥CD,∠C=125°,∴∠BFE=125°.∴∠E=∠BFE﹣∠A=125°﹣45°=80°.
故选:B.
6.解:三角形的重心是三角形三条中线的交点.
故选:D.
7.解:A、添加AO=BO不能判定△ABC≌△DCB,故此选项不合题意;
B、添加∠ACB=∠DBC不能判定△ABC≌△DCB,故此选项不合题意;
C、添加AC=DB可利用SSS判定△ABC≌△DCB,故此选项符合题意;
D、添加BO=CO不能判定△ABC≌△DCB,故此选项不合题意;
故选:C.
8.解:作AF⊥BC.
∵S△ADB=BD×AF×=,
S△ADC=CD×AF×=S,
又∵AD为△ABC中BC边上的中线,
∴BD=CD,
∴S△ADB=S△ADC,
同理,
∴S△ABE=S△ABC,
即S1=S,
∴S=4S1,
故选:B.
9.解:若BD=CE,则依据AB=AC,可得AD=AE,
由AB=AC,∠A=∠A,AE=AD,可得△ABE≌△ACD(SAS),
故A选项能判断△ABE≌△ACD;
若BE=CD,则不能得到△ABE≌△ACD,
故B选项不能判断△ABE≌△ACD;
若AD=AE,则可得△ABE≌△ACD(SAS),
故C选项能判断△ABE≌△ACD;
若∠B=∠C,则由∠B=∠C,AB=AC,∠A=∠A,可得△ABE≌△ACD(ASA),
故D选项能判断△ABE≌△ACD;
故选:B.
10.解:∵∠A+∠B+∠C=180°,∠C=90°,
∴∠A+∠B=180°﹣∠C=90°,
∴∠A和∠B互余.
故选:D.
11.解:A.∵2+3>4,∴能构成三角形;
B.∵3+4<8,∴不能构成三角形;
C.∵4+4=8,∴不能构成三角形;
D.∵5+5<11,∴不能构成三角形.
故选:A.
12.解:锐角三角形有三条高,高都在三角形内部;
直角三角形有两条高即三角形的两条直角边,一条在内部;
钝角三角形有三条高,一条高在三角形内部,另外两条高在三角形外部,
所以A、B、C都错误,
只有D是正确的.
故选:D.
13.解:∵在△ABC中,∠A=50°,∠C=72°,
∴∠ABC=180°﹣50°﹣72°=58°,
∵BD是△ABC的一条角平分线,
∴∠ABD=29°,
故选:A.
14.解:A、不是全等形,故此选项错误;
B、不是全等形,故此选项错误;
C、是全等形,故此选项正确;
D、不是全等形,故此选项错误;
故选:C.
15.解:伸缩门可自由伸缩,开关方便,随处可见,它凸显了四边形的不稳定性.
故选:B.
二.填空题
16.解:∵AB⊥BD,ED⊥BD,
∴∠ABD=∠EDC=90°,
在△EDC和△ABC中,
,
∴△EDC≌△ABC(ASA).
故答案为:ASA.
17.解:要想知道M与F的距离,只需要测出线段EM的长度.
理由是依据SAS可以证明△BEM≌△CFM,从而由全等三角形对应边相等得出.
证明:连接EF
∵AB∥CD,(已知)
∴∠B=∠C(两线平行内错角相等).
∵M是BC中点
∴BM=CM,
∵在△BEM和△CFM中,
∴△BEM≌△CFM(SAS).
∴CF=BE(对应边相等).
故答案为:EM,SAS,△BEM≌△CFM.
18.解:补充的条件是AB=CD,
理由是:在△ABD和△CDB中,
,
∴△ABD≌△CDB(SSS),
故答案为:AB=CD(答案不唯一).
19.解:(1)根据三角形的角平分线的概念,知AD是△ABC的角平分线,故此说法正确;
(2)根据三角形的中线的概念,知BG是△ABD的边AD上的中线,故此说法不正确;
(3)根据三角形的高的概念,知CH为△ACD的边AD上的高,故此说法不正确;
(4)根据三角形的角平分线和高的概念,知AH是△ACF的角平分线和高线,故此说法正确.
故答案为(1)(4).
三.解答题
20.已知:AD和A′D′分别为△ABC和△A′B′C′中线,且AD=A′D′,AB=A′B′,BC=B′C′,如图,
求证:△ABC≌△A′B′C′.
证明:∵AD和A′D′分别为△ABC和△A′B′C′中线,
∴BD=BC,B′D′=B′C′,
而BC=B′C′,
∴BD=B′D′,
在△ABD和△A′B′D′中
,
∴△ABD≌△A′B′D′(SSS),
∴∠B=∠B′,
在△ABC和△A′B′C′中
,
∴△ABC≌△A′B′C′(SAS),
即有两条边和其中一条边上的中线对应相等的两个三角形全等.
21.证明:在△AEB和△DEC中
,
∴△AEB≌△DEC(SAS),
∴∠BAE=∠CDE,AB=CD,
∵EA=ED,EB=EC,
∴AC=BD,
在△ABC和△DCB中
∴△ABC≌△DCB(SAS).
22.解:(1)∠ACB=90°,∠ADC=90°,
∴图中有3个直角三角形,分别是△ACD,△BCD,△ABC.
(2)∵∠ADC=90°,
∴∠1+∠A=90°,
∵∠1+∠2=90°,
∴∠2=∠A,∠1=∠B.
23.解:(1)如图所示:
(2) BC AD= AB CE,
×9×2=×6 CE,
解得:CE=3.
24.解:(1)如图所示,AE即为所求:
(2)∵AE平分∠CAD,
∴∠DAE=∠EAC,
∵∠B=∠C,∠DAC=∠B+∠C,
∴∠DAE=∠B=∠C=∠EAC,
∴AE∥BC.
25.解:∵△ADE是等边三角形,
∴∠D=∠E=60°,
∵DE∥BC,
∴∠AMN=∠D,∠ANM=∠E,
∴∠AMN=∠ANM=60°,
∴∠AMB=∠ANC=120°,
∵AB=AC,
∴∠B=∠C,
在△ABM和△ACN中,
∴△ABM≌△ACN,
∴BM=CN.
