基本不等式(1)[上学期]
图片预览

文档简介
§3.4基本不等式
滕州七中 刘海洋
2005.10
§3.4基本不等式
教学目标:
1、 探索并了解基本不等式的证明过程;
2、 会用基本不等式解决简单的判断代数式的大小关系。
教学重点:
应用数形结合的思想理解基本不等式,并从不同角度探索基本不等式。
教学难点:
用基本不等式判断代数式的大小关系。
教学过程:
1、 引入:
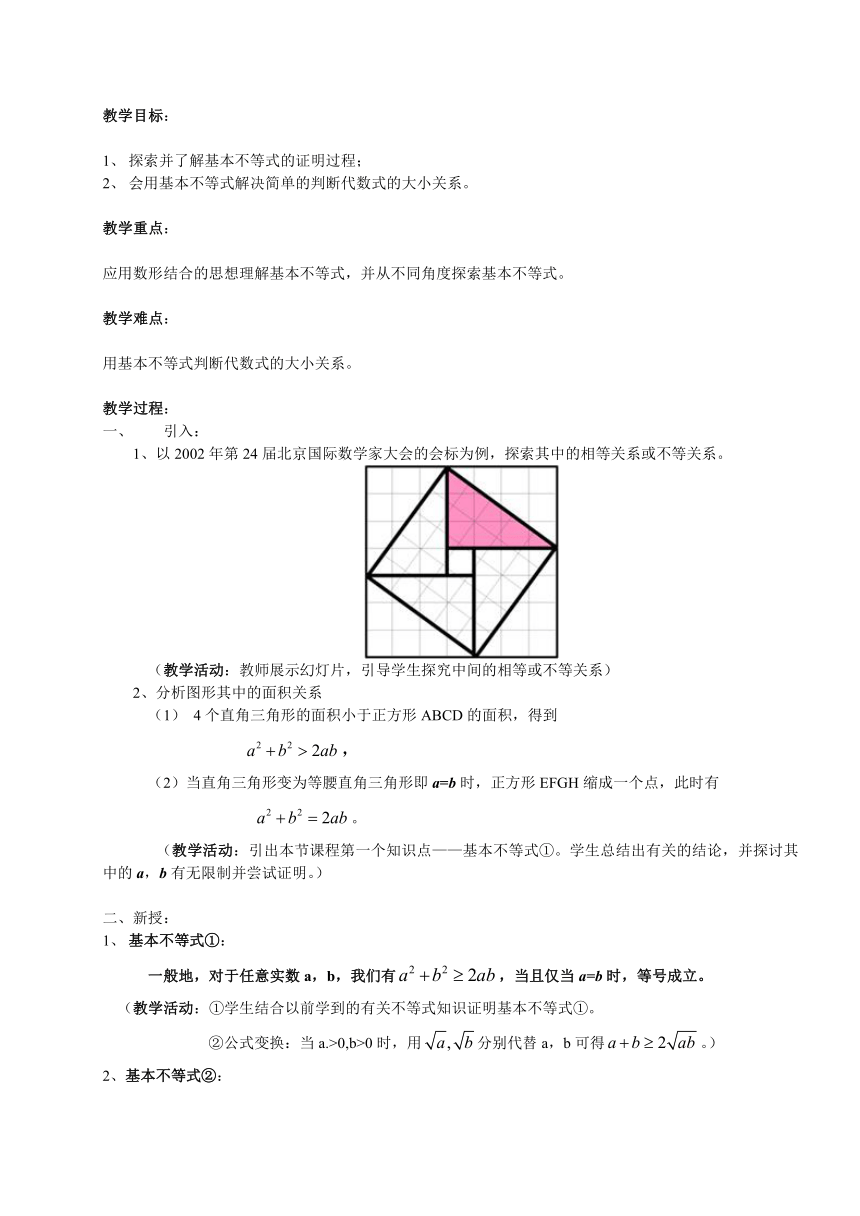
1、以2002年第24届北京国际数学家大会的会标为例,探索其中的相等关系或不等关系。
(教学活动:教师展示幻灯片,引导学生探究中间的相等或不等关系)
2、分析图形其中的面积关系
(1) 4个直角三角形的面积小于正方形ABCD的面积,得到
,
(2)当直角三角形变为等腰直角三角形即a=b时,正方形EFGH缩成一个点,此时有
。
(教学活动:引出本节课程第一个知识点——基本不等式①。学生总结出有关的结论,并探讨其中的a,b有无限制并尝试证明。)
二、新授:
1、 基本不等式①:
一般地,对于任意实数a,b,我们有,当且仅当a=b时,等号成立。
(教学活动:①学生结合以前学到的有关不等式知识证明基本不等式①。
②公式变换:当a.>0,b>0时,用分别代替a,b可得。)
2、基本不等式②:
,当且仅当a=b时,等号成立。
(教学活动:①学生体会基本不等式②及其形式;②尝试证明,通过证明体会分析法的思想。)
(1)法一:证明: 要证 ①
只要证 ②
要证②,只要证 ③
要证③,只要证 ④
显然,④是成立的。当且仅当a=b时,④中的等号成立。
法二:(作差比较法)
(2)两个正数的算术平均数和几何平均数
称为正数a,b的算术平均数;则为它们的几何平均数。
3、 探究基本不等式②的几何解释
由ΔACD∽ΔBCD,可得;由于CD(半弦)小于或等于圆的半径,用不等式表示为。
(教学活动:学生分析上图,得到有关的几何解释。)
4、 比较两个基本不等式的有关限制条件来认识两个基本不等式应用范围。
三、例题讲解:
应用一:利用基本不等式判断代数式的大小关系
例1、设a>0,b>0,给出下列不等式
其中恒成立的 (1)(2)(3) 。
练习:(2000全)若,则( B )
A、R应用二:解决最大(小)值问题
例2、(1)用篱笆围一个面积为100m2的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短。最短篱笆是多少?
(2)一段长为36m的篱笆围成一矩形菜园,问这个矩形的长、宽各为多少时,菜园的面积最大。最大面积是多少?
解:(1)设矩形菜园的长为x m,宽为y m,则x y =100,篱笆的长为2(x+y)m。
由
可得
。
等号当且仅当 x = y时成立,此时x = y =10。因此,这个矩形的长、宽都为10m时,所用篱笆最短,最短篱笆为40m。
(2)设矩形菜园的长为x m,宽为y m,则2(x+y)=36,x+y=18,矩形菜园的面积为xym2。
由 ,
可得 x y≤81,
当且仅当 x = y,即 x = y =10时,等号成立。
因此,这个矩形的长、宽都为9m时,菜园的面积最大,最大面积是81m2。
(教学活动:学生回顾题目,得出结论。)
结论:
(1)两个正数和为定值,积有最大值。
(2)两个正数积为定值,和有最小值。
注意:
“一正,二定,三相等”。
练习: 1、当x>0时,的最小值是 2 ,此时x= 1 。
2、(04重庆)当x>0时,,则x y的最小值是 6 。
思考:上面练习1中的x>0换成x<0则表达式是何种情况?
四、小结
1、 两个基本不等式
2、 两种简单应用(一正,二定,三相等)
五、作业
教材P113A组第1题
A
D
B
E
C
b
a
学标练课
教案
滕州七中 刘海洋
2005.10
§3.4基本不等式
教学目标:
1、 探索并了解基本不等式的证明过程;
2、 会用基本不等式解决简单的判断代数式的大小关系。
教学重点:
应用数形结合的思想理解基本不等式,并从不同角度探索基本不等式。
教学难点:
用基本不等式判断代数式的大小关系。
教学过程:
1、 引入:
1、以2002年第24届北京国际数学家大会的会标为例,探索其中的相等关系或不等关系。
(教学活动:教师展示幻灯片,引导学生探究中间的相等或不等关系)
2、分析图形其中的面积关系
(1) 4个直角三角形的面积小于正方形ABCD的面积,得到
,
(2)当直角三角形变为等腰直角三角形即a=b时,正方形EFGH缩成一个点,此时有
。
(教学活动:引出本节课程第一个知识点——基本不等式①。学生总结出有关的结论,并探讨其中的a,b有无限制并尝试证明。)
二、新授:
1、 基本不等式①:
一般地,对于任意实数a,b,我们有,当且仅当a=b时,等号成立。
(教学活动:①学生结合以前学到的有关不等式知识证明基本不等式①。
②公式变换:当a.>0,b>0时,用分别代替a,b可得。)
2、基本不等式②:
,当且仅当a=b时,等号成立。
(教学活动:①学生体会基本不等式②及其形式;②尝试证明,通过证明体会分析法的思想。)
(1)法一:证明: 要证 ①
只要证 ②
要证②,只要证 ③
要证③,只要证 ④
显然,④是成立的。当且仅当a=b时,④中的等号成立。
法二:(作差比较法)
(2)两个正数的算术平均数和几何平均数
称为正数a,b的算术平均数;则为它们的几何平均数。
3、 探究基本不等式②的几何解释
由ΔACD∽ΔBCD,可得;由于CD(半弦)小于或等于圆的半径,用不等式表示为。
(教学活动:学生分析上图,得到有关的几何解释。)
4、 比较两个基本不等式的有关限制条件来认识两个基本不等式应用范围。
三、例题讲解:
应用一:利用基本不等式判断代数式的大小关系
例1、设a>0,b>0,给出下列不等式
其中恒成立的 (1)(2)(3) 。
练习:(2000全)若,则( B )
A、R
例2、(1)用篱笆围一个面积为100m2的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短。最短篱笆是多少?
(2)一段长为36m的篱笆围成一矩形菜园,问这个矩形的长、宽各为多少时,菜园的面积最大。最大面积是多少?
解:(1)设矩形菜园的长为x m,宽为y m,则x y =100,篱笆的长为2(x+y)m。
由
可得
。
等号当且仅当 x = y时成立,此时x = y =10。因此,这个矩形的长、宽都为10m时,所用篱笆最短,最短篱笆为40m。
(2)设矩形菜园的长为x m,宽为y m,则2(x+y)=36,x+y=18,矩形菜园的面积为xym2。
由 ,
可得 x y≤81,
当且仅当 x = y,即 x = y =10时,等号成立。
因此,这个矩形的长、宽都为9m时,菜园的面积最大,最大面积是81m2。
(教学活动:学生回顾题目,得出结论。)
结论:
(1)两个正数和为定值,积有最大值。
(2)两个正数积为定值,和有最小值。
注意:
“一正,二定,三相等”。
练习: 1、当x>0时,的最小值是 2 ,此时x= 1 。
2、(04重庆)当x>0时,,则x y的最小值是 6 。
思考:上面练习1中的x>0换成x<0则表达式是何种情况?
四、小结
1、 两个基本不等式
2、 两种简单应用(一正,二定,三相等)
五、作业
教材P113A组第1题
A
D
B
E
C
b
a
学标练课
教案
