基本不等式求最值[下学期]
图片预览





文档简介
课件13张PPT。应用基本不等式求最值顺德伦教中学:王新骇课前练习:典型例题:例1:求证:
(1)在所有周长相同的矩形中,
正方形的面积最大;
(2)在所有面积相同的矩形中,
正方形的周长最短。分析:设矩形的长为 ,宽为 ,那么该矩形的周长
为 ,面积为 ,这样问题就转化为:
(1)如果 (从而 )为定值,那么
正数 有什么关系时, 最大。
(2)如果 为定值,那么正数 有什么关系时,
(从而 )最小。小结:对于两个正实数 ,
如果它们的和S是定值,则当且仅当 时,
它们的积P取得最大值。如果它们的积P是定值,则当且仅当 时,
它们的和S取得最小值。(定和求大积)(定积求小和)1)若x>0,f(x)= 的最小值为_______;此时x=_______.
若x<0,f(x)= 的最大值为_______;
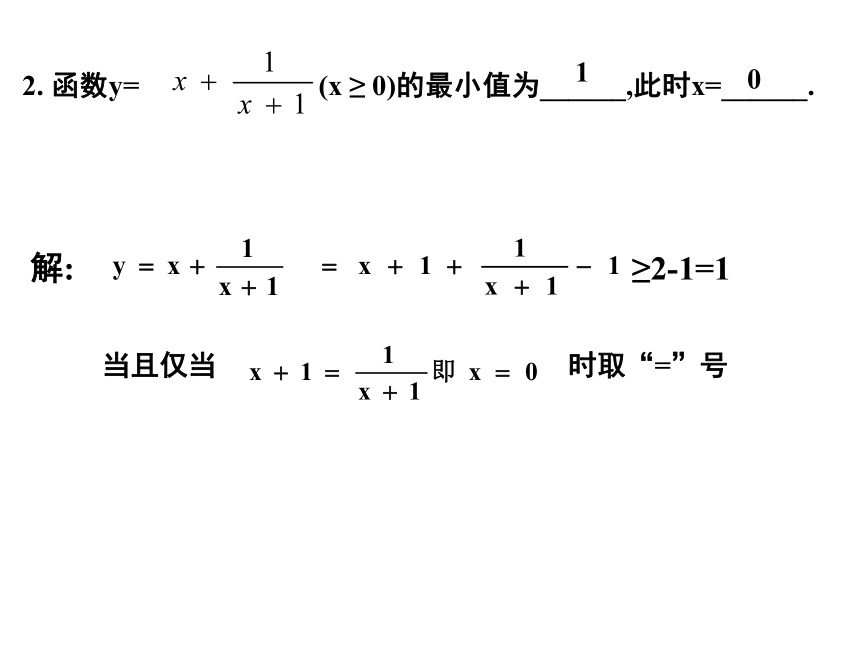
此时x=_______.122-12-2练习:2. 函数y= (x ≥ 0)的最小值为______,此时x=______.解:≥2-1=1当且仅当 时取“=”号013.求函数 的最小值.当且仅当 时取等号错解:一正,二定,三相等③必须有自变量值能使函数取到 = 号.①各项必须为正;②含变数的各项和或积必须为定值;小结:利用均值不等式求函数最值应注意:3.求函数 的最小值.利用函数 (t>0)的单调性.单调递减单调递增依据:正解:阅读下题的各种解法,指出有错误的地方例2:还有其它方法吗?例3:已知 且 , 求:x+y的最小值?还有其他方法吗?当且仅当 时取“=”号2.求函数 的最小值.即当 时,函数的最小值为解:1:求函数 的最大值,
并求出相应x的值.巩固练习:
(1)在所有周长相同的矩形中,
正方形的面积最大;
(2)在所有面积相同的矩形中,
正方形的周长最短。分析:设矩形的长为 ,宽为 ,那么该矩形的周长
为 ,面积为 ,这样问题就转化为:
(1)如果 (从而 )为定值,那么
正数 有什么关系时, 最大。
(2)如果 为定值,那么正数 有什么关系时,
(从而 )最小。小结:对于两个正实数 ,
如果它们的和S是定值,则当且仅当 时,
它们的积P取得最大值。如果它们的积P是定值,则当且仅当 时,
它们的和S取得最小值。(定和求大积)(定积求小和)1)若x>0,f(x)= 的最小值为_______;此时x=_______.
若x<0,f(x)= 的最大值为_______;
此时x=_______.122-12-2练习:2. 函数y= (x ≥ 0)的最小值为______,此时x=______.解:≥2-1=1当且仅当 时取“=”号013.求函数 的最小值.当且仅当 时取等号错解:一正,二定,三相等③必须有自变量值能使函数取到 = 号.①各项必须为正;②含变数的各项和或积必须为定值;小结:利用均值不等式求函数最值应注意:3.求函数 的最小值.利用函数 (t>0)的单调性.单调递减单调递增依据:正解:阅读下题的各种解法,指出有错误的地方例2:还有其它方法吗?例3:已知 且 , 求:x+y的最小值?还有其他方法吗?当且仅当 时取“=”号2.求函数 的最小值.即当 时,函数的最小值为解:1:求函数 的最大值,
并求出相应x的值.巩固练习:
