山东省菏泽市单县第五高级中学校2022-2023学年高二上学期9月开学考试数学试题(PDF版含答案)
文档属性
| 名称 | 山东省菏泽市单县第五高级中学校2022-2023学年高二上学期9月开学考试数学试题(PDF版含答案) |  | |
| 格式 | |||
| 文件大小 | 569.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-09 17:21:50 | ||
图片预览


文档简介
高二年级秋季开学考试
数学试题
一、单项选择题:本题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.若复数 z满足 z·(1-2i)=i(i 是虚数),则复数 z在复平面内对应的点在( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.如果你正在筹划一次聚会,想知道该准备多少瓶饮料,你最希望得到所有客人需要
饮料数量的( ).
A.四分位数 B.中位数 C.众数 D.均值
3.《张丘建算经》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有方锥
下广二丈,高三丈,欲斩末为方亭;令上方六尺;问斩高几何?”其意思为:已知方锥(即
正四棱锥)下底边长为 20 尺,高为 30 尺;现欲从方锥上面截去一段,使之成为方亭(即正四
棱台),且使方亭上底边长为 8 尺(如图所示),则截去小方锥的高为( ).
A.24 尺 B.18 尺 C.12 尺 D.6 尺
4.已知 10 个产品中有 3 个次品,现从其中抽出若干
个产品,要使这 3 个次品全部被抽出的概率不小
于 0.6,则至少应抽出的产品数为( ).
A.7 B.8 C.9 D.10
5..打靶时,甲命中目标的概率为 0.8,乙命不中目标的概率为 0.3.若两人同时射击,
则他们同时命中目标的概率为( ).
14 12 12 3
A. B. C. D.
25 25 50 5
6.已知向量 a=(2,1),a·b=10,│a+b│= 5 2 ,则│b│=( ).
A. 5 B.10 C. 5 D. 10
7.若平面α过正方体 ABCD-A1B1C1D1 的顶点 A,平面α∥平面 A1BD,平面α 平面 ABCD
=l,则直线 l与直线 CD1所成的角为( ).
A.30° B.45° C.60° D.90°
8.如图,在棱长为 1 的正方体 ABCD-A1B1C1D1中,点 E,F分别是棱 BC,CC1 的中点,
P是底面 ABCD(含边界)上一动点,满足 A1P⊥EF,则线段 A1P长度的取值范围是( ).
A 1 5 5
3
.[ , ] B.[ , ] C.[1,
2 3
] D.[ 2 , 3 ]
2 2
二、多项选择题:本题共 4 小题,每小题 5 分,共 20 分.
在每小题给出的四个选项中,有多项符合题目要求.全部选对
的得 5 分,部分选对的得 3 分,有选错的得 0 分.
9.下列命题中正确的是( ).
知不足者好学 1 耻下问者自满
A.如果一个平面内有两条直线都平行于另一个平面,那么这两个平面平行
B.如果一个平面内的任何一条直线都平行于另一个平面,那么这两个平面平行
C.分别在两个平行平面内的两条直线互相平行
D.过平面外一点有且仅有一个平面与已知平面平行
10.下列命题中正确的是( ).
A.对任意复数 z,都有 z2≥0 B.对任意复数 z1,z2,都有∣z1+z2∣=∣z1∣+∣z2∣
1
C.若复数 z满足 z R,则 z R D.若复数 z满足 R,则 z Rz
11.已知 A(2,1),B(5,2),C(4,4),D(1,3),下述四个结论中正确的是( ).
uuur uuur
A. AB AC B.四边形 ABCD为平行四边形
uuur uuur 3 uuur uuurC. AC与 BD夹角的余弦值为 D. | AB AC |= 416
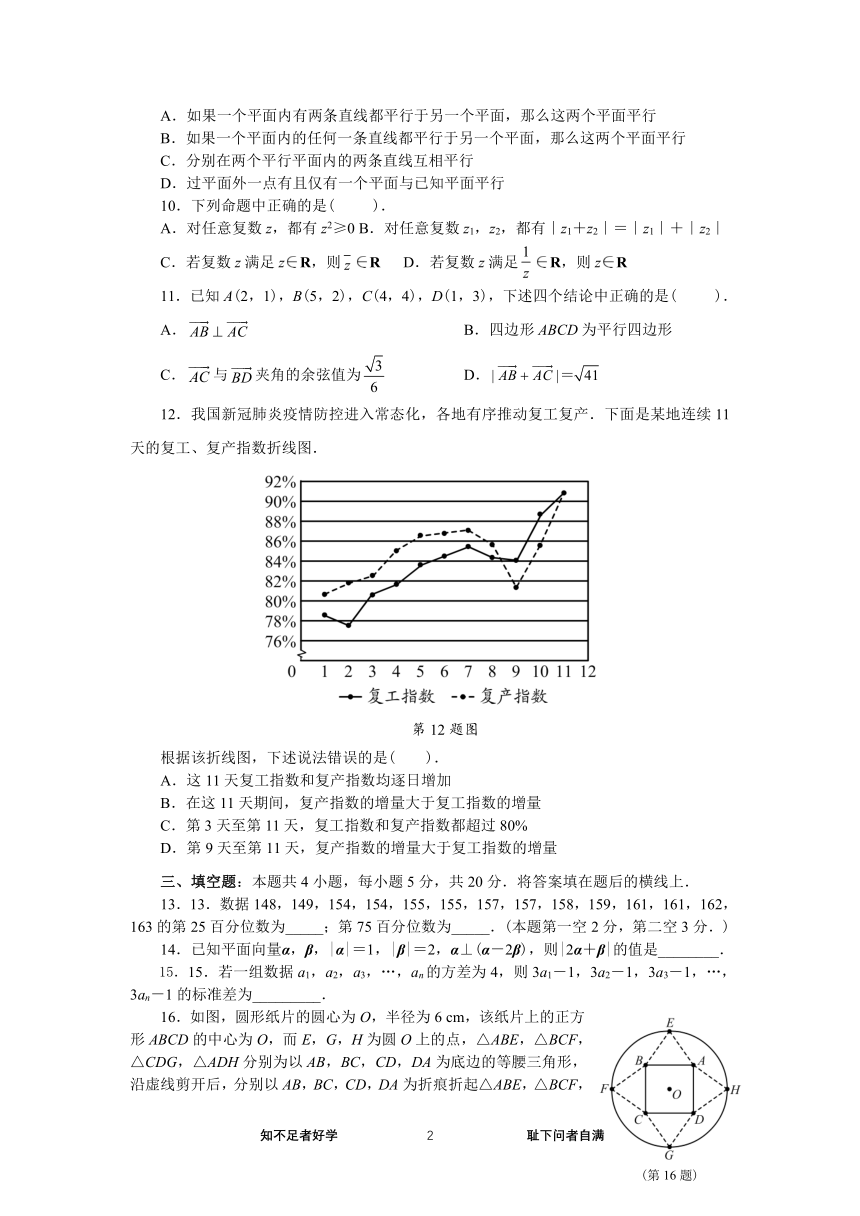
12.我国新冠肺炎疫情防控进入常态化,各地有序推动复工复产.下面是某地连续 11
天的复工、复产指数折线图.
第 12 题图
根据该折线图,下述说法错误的是( ).
A.这 11 天复工指数和复产指数均逐日增加
B.在这 11 天期间,复产指数的增量大于复工指数的增量
C.第 3 天至第 11 天,复工指数和复产指数都超过 80%
D.第 9 天至第 11 天,复产指数的增量大于复工指数的增量
三、填空题:本题共 4 小题,每小题 5 分,共 20 分.将答案填在题后的横线上.
13.13.数据 148,149,154,154,155,155,157,157,158,159,161,161,162,
163 的第 25 百分位数为_____;第 75 百分位数为_____.(本题第一空 2 分,第二空 3 分.)
14.已知平面向量α,β,|α|=1,|β|=2,α⊥(α-2β),则|2α+β|的值是________.
15.15.若一组数据 a1,a2,a3,…,an的方差为 4,则 3a1-1,3a2-1,3a3-1,…,
3an-1 的标准差为_________.
16.如图,圆形纸片的圆心为 O,半径为 6 cm,该纸片上的正方
形 ABCD的中心为 O,而 E,G,H为圆 O上的点,△ABE,△BCF,
△CDG,△ADH分别为以 AB,BC,CD,DA为底边的等腰三角形,
沿虚线剪开后,分别以 AB,BC,CD,DA为折痕折起△ABE,△BCF,
知不足者好学 2 耻下问者自满
(第 16 题)
△CDG,△ADH,使得 E,F,G,H重合,得到一个四棱锥.当该四棱锥的侧面积是底面
积的 2 倍时,四棱锥的外接球的体积为_______.
四、解答题:本题共 6 小题,共 70 分.解答应写出文字说明、证明过程或演算步骤.
17.(10 分)已知 a,b,c 是同一平面内的三个向量,其中 a=(1,2).
(1)若 c=(3 +1, -3),且 c∥a,求 的值;
(2)若 b=(1,m)(m<0),且 a+2b 与 a-2b 垂直,求 a 与 b 的夹角θ.
18.(12 分)某校在高三年级学生一次数学考试后,对 90 分以上(含 90 分)的成绩进行统
计,其频率分布直方图如图所示,若 130~140 分数段的人数为 2 人.
(1)请估计一下这组数据的平均数 M;
(2)现根据考试成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、
第五组)中任意选出两人,形成“帮扶学习小组”.若选出的两人成绩之差大于 20,则称这
两人为“黄金搭档组”,试求选出的两人为“黄金搭档组”的概率.
19.(12 分)如图,在四棱锥 A-BCDE中,BE∥CD,BE⊥BC,AB=AC,平面 BCDE⊥平
面 ABC,M为 BC的中点.
(1)若 N是线段 AE的中点,求证:MN∥平面 ACD;
(2)若 BE=1,BC=2,CD=3,求证:DE⊥平面 AME.
(第 18 题)
知不足者好学 3 耻下问者自满
20.(12 分)△ABC的内角 A,B,C的对边分别为 a,b,c,cos A+ 3 sin A=0,a= 2 7 ,
b= 2 3 .
(1)求 c;
(2)设 D为 BC边上一点,且 AD⊥AC,求△ABD的面积.
21.(12 分)乒乓球比赛规则规定:一局比赛,双方比分在 10 平前,一方连续发球 2 次
后,对方再连续发球 2 次,依次轮换.每次发球,胜方得 1 分,负方得 0 分.设在甲、乙的
比赛中,每次发球,发球方得 1 分的概率为 0.6,各次发球的胜负结果相互独立.甲、乙的
一局比赛中,甲先发球.
(1)求开始第 4 次发球时,甲、乙的比分为 1 比 2 的概率;
(2)求开始第 5 次发球时,甲得分领先的概率.
22.(12 分)如图,在直三棱柱 ABC-A1B1C1 中,AB⊥BC,AA1=AC=2,BC=1,E,F
分别为 A1 C1,BC的中点.
(1)求证:平面 ABE⊥平面 B1BCC1;
(2)求证:在棱 AC上存在一点 M,使得平面 C1FM∥平面 ABE;
(3)求三棱锥 E-ABC的体积.
(第 21 题
知不足者好学 4 耻下问者自满
高二年级秋季开学数学试题
参考答案
一、单项选择题 1.B.2.D.3.C.4.C.5.A.6.A.7.C.8.D.
二、多项选择题 9.BD. 10.CD.11.BCD.12.AB.
三、填空题
13 14 15 16 500 3π.154. . 10 . .6; . cm3 .
27
提示:如图,连接 OE,交 AB于点 I,设 E,F,G,H重合于点 P,正方形的边长为
x x
x(x>0),则 OI= ,IE=6- .
2 2
(第 16 题)
∵ 该四棱锥的侧面积是底面积的 2 倍,
x x
∴ 4× (6- )=2x2,解得 x=4.
2 2
设该四棱锥的外接球的球心为 Q,半径为 R,则 OC= 2 2 ,OP= 2 3 ,R2=( 2 3 -
5
R 2 500 3π) +( 2 2 )2,解得 R= .∴ 外接球的体积 V= cm3.3 27
四、解答题
17.解:(1)因为 c=(3 +1, -3),且 c∥a,所以(3 +1)×2-( -3)×1=0,
解得 =-1;--------------------------4 分
a+2b=(3, 2+2m),
(2) 由题意,可知 a 2b 1 2 2m -----------------------------6 分 - =(-, - ).
因为 a+2b 与 a-2b 垂直,
1 1
所以(a+2b)·(a-2b)=0,解得 m=- ,则 b=(1,- ),--------------9 分
2 2
知不足者好学 5 耻下问者自满
π
所以 a·b=0,于是θ= .-----------------------------------------10 分
2
18.解:(1)M=95×0.01×10+105×0.025×10+115×0.045×10+125×0.015×10+
135×0.005×10=113(分).-------------------------------3 分
(2)设 90~140 分之间的人数是 n,由 130~140 分数段的人数为 2 人,可知 0.005×10×n
=2,解得 n=40.---------------------------5 分
依题意,第一组共有 40×0.01×10=4(人),记作 A1,A2,A3,A4;第五组共有 2 人,
记作 B1,B2.从第一组和第五组中任意选出两人,样本空间为{(A1,A2),(A1,A3),(A1,
A4),(A1,B1),(A1,B2),(A2,A1),(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,
A1),(A3,A2),(A3,A4),(A3,B1),(A3,B2),(A4,A1),(A4,A2),(A4,A3),(A4,
B1),(A4,B2),(B1,A1),(B1,A2),(B1,A3),(B1,A4),(B1,B2),(B2,A1),(B2,
A2),(B2,A3),(B2,A4),(B2,B1)},共有 30 个等可能的样本点.--------10 分
用事件 A表示“选出的两人为‘黄金搭档组’”.若两人成绩之差大于 20,则两人分
8
别来自于第一组和第五组,共有 16 个样本点,故 P(A)= .--------12 分
15
19.解:(1)取 AB的中点 H,连接 MH,NH.∵ N是 AE的中点,∴NH∥BE.
又 BE∥CD,∴NH∥CD.又∵NH 平面 ACD,∴NH∥平面 ACD.
同理可证,MH∥平面 ACD.而 MH NH=H,
∴ 平面 MNH∥平面 ACD,
∴ MN∥平面 ACD.--------------------------5 分
(2)连接 AM,DM,EM,由 AB=AC,M为 BC的中点,得 AM⊥BC.
又平面 BCDE⊥平面 ABC,平面 BCDE 平面 ABC=BC,AM 平面 ABC,∴AM⊥平
面 BCDE,∴AM⊥DE.
1
在 Rt△EBM中,BE=1,BM= BC=1,∴EM= .
2 2
1
在 Rt△DCM中,CD=3,CM= BC=1,∴DM= 10 .2
在直角梯形 BCDE中,可得 DE= (CD-BE)2+BC 2 = 2 2 ,
(第 18 题)
∴ EM 2+ DE 2 =DM 2 ,∴EM⊥DE.
又∵AM EM=M,∴ DE⊥平面 AME.-------------------12 分
5π
120 3.解:(1)由已知可得 tan A=- ,所以 A= .
3 6
知不足者好学 6 耻下问者自满
5π
在△ABC中,由余弦定理得 28=12+c2- 4 3 ccos ,即 c2+6c-16=0,6
解得 c=-8(舍去),c=2.--------6 分
π π
(2)由题设可得∠CAD= ,所以∠BAD=∠BAC-∠CAD= .
2 3
1
S ACgADVACD 2 1 5π
故 S = 1 π =2.又 S△ABC= ×2× 2 3 sin = 3 ,VABD ABgADgsin 2 6
2 3
3
所以 S△ABD= .-------------------------12 分3
21.解:用事件 Ai表示“第 1 次和第 2 次这两次发球,甲共得 i分”,i=0,1,2;Bi
表示“第 3 次和第 4 次这两次发球,甲共得 i分”,i=0,1,2;A表示“第 3 次发球,甲
得 1 分”;B表示“开始第 4 次发球时,甲、乙的比分为 1 比 2”;C=“开始第 5 次发球
时,甲得分领先”---------------------2 分.
(1)因为 P(A)=0.4,P(A0)=0.42=0.16,P(A1)=2×0.6×0.4=0.48,B=A0A+ A1A,
所以 P(B)=P(A0A+ A1A )=P(A0A)+P( A1A )=P(A0)P(A)+P(A1)P( A )=0.352.---6 分
(2)因为 P(B0)=0.62=0.36,P(B1)=2×0.4×0.6=0.48,P(B2)=0.42=0.16,
P(A2)=0.62=0.36.C=A1B2+A2B1+A2B2,
所以 P(C)=P(A1B2+A2B1+A2B2)=P(A1B2)+P(A2B1)+P(A2B2)
=P(A1)P(B2)+P(A2)P(B1)+P(A2)P(B2)=0.307 2.-----------------------12 分
22.解:(1)在直三棱柱 ABC-A1B1C1中,∵BB1⊥平面 ABC,
23.∴BB1⊥AB.
又∵AB⊥BC,BC BB1=B,
∴AB⊥平面 B1BCC1.
∴平面 ABE⊥平面 B1BCC1.--4 分
(3) 取 AC中点 M,连接 C1M,FM,
(4) ∵F为 BC的中点,∴FM∥AB.
∵AB 平面 ABE,FM 平面 ABE,∴ FM∥平面 ABE.
∵AM∥C1M,AM=C1M,
∴四边形 AMC1E为平行四边形.
∴C1M∥AE,C1M 平面 ABE.
(第 21 题)
知不足者好学 7 耻下问者自满
∴C1M∥平面 ABE.
∵C1M FM=M,
∴平面 C1FM∥平面 ABE,
即存在 AC的中点 M使得平面 C1FM∥平面 ABE.---------9 分
(3)点 E到底面的距离即为侧棱长 AA1=2.
∵在 Rt△ABC中,AC=2,BC=1,AB⊥BC,
S 1 3∴ AB= 3 , ABC= ABgBC= .2 2
V 3∴ E ABC= .-----------------------12 分3
知不足者好学 8 耻下问者自满
数学试题
一、单项选择题:本题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.若复数 z满足 z·(1-2i)=i(i 是虚数),则复数 z在复平面内对应的点在( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.如果你正在筹划一次聚会,想知道该准备多少瓶饮料,你最希望得到所有客人需要
饮料数量的( ).
A.四分位数 B.中位数 C.众数 D.均值
3.《张丘建算经》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有方锥
下广二丈,高三丈,欲斩末为方亭;令上方六尺;问斩高几何?”其意思为:已知方锥(即
正四棱锥)下底边长为 20 尺,高为 30 尺;现欲从方锥上面截去一段,使之成为方亭(即正四
棱台),且使方亭上底边长为 8 尺(如图所示),则截去小方锥的高为( ).
A.24 尺 B.18 尺 C.12 尺 D.6 尺
4.已知 10 个产品中有 3 个次品,现从其中抽出若干
个产品,要使这 3 个次品全部被抽出的概率不小
于 0.6,则至少应抽出的产品数为( ).
A.7 B.8 C.9 D.10
5..打靶时,甲命中目标的概率为 0.8,乙命不中目标的概率为 0.3.若两人同时射击,
则他们同时命中目标的概率为( ).
14 12 12 3
A. B. C. D.
25 25 50 5
6.已知向量 a=(2,1),a·b=10,│a+b│= 5 2 ,则│b│=( ).
A. 5 B.10 C. 5 D. 10
7.若平面α过正方体 ABCD-A1B1C1D1 的顶点 A,平面α∥平面 A1BD,平面α 平面 ABCD
=l,则直线 l与直线 CD1所成的角为( ).
A.30° B.45° C.60° D.90°
8.如图,在棱长为 1 的正方体 ABCD-A1B1C1D1中,点 E,F分别是棱 BC,CC1 的中点,
P是底面 ABCD(含边界)上一动点,满足 A1P⊥EF,则线段 A1P长度的取值范围是( ).
A 1 5 5
3
.[ , ] B.[ , ] C.[1,
2 3
] D.[ 2 , 3 ]
2 2
二、多项选择题:本题共 4 小题,每小题 5 分,共 20 分.
在每小题给出的四个选项中,有多项符合题目要求.全部选对
的得 5 分,部分选对的得 3 分,有选错的得 0 分.
9.下列命题中正确的是( ).
知不足者好学 1 耻下问者自满
A.如果一个平面内有两条直线都平行于另一个平面,那么这两个平面平行
B.如果一个平面内的任何一条直线都平行于另一个平面,那么这两个平面平行
C.分别在两个平行平面内的两条直线互相平行
D.过平面外一点有且仅有一个平面与已知平面平行
10.下列命题中正确的是( ).
A.对任意复数 z,都有 z2≥0 B.对任意复数 z1,z2,都有∣z1+z2∣=∣z1∣+∣z2∣
1
C.若复数 z满足 z R,则 z R D.若复数 z满足 R,则 z Rz
11.已知 A(2,1),B(5,2),C(4,4),D(1,3),下述四个结论中正确的是( ).
uuur uuur
A. AB AC B.四边形 ABCD为平行四边形
uuur uuur 3 uuur uuurC. AC与 BD夹角的余弦值为 D. | AB AC |= 416
12.我国新冠肺炎疫情防控进入常态化,各地有序推动复工复产.下面是某地连续 11
天的复工、复产指数折线图.
第 12 题图
根据该折线图,下述说法错误的是( ).
A.这 11 天复工指数和复产指数均逐日增加
B.在这 11 天期间,复产指数的增量大于复工指数的增量
C.第 3 天至第 11 天,复工指数和复产指数都超过 80%
D.第 9 天至第 11 天,复产指数的增量大于复工指数的增量
三、填空题:本题共 4 小题,每小题 5 分,共 20 分.将答案填在题后的横线上.
13.13.数据 148,149,154,154,155,155,157,157,158,159,161,161,162,
163 的第 25 百分位数为_____;第 75 百分位数为_____.(本题第一空 2 分,第二空 3 分.)
14.已知平面向量α,β,|α|=1,|β|=2,α⊥(α-2β),则|2α+β|的值是________.
15.15.若一组数据 a1,a2,a3,…,an的方差为 4,则 3a1-1,3a2-1,3a3-1,…,
3an-1 的标准差为_________.
16.如图,圆形纸片的圆心为 O,半径为 6 cm,该纸片上的正方
形 ABCD的中心为 O,而 E,G,H为圆 O上的点,△ABE,△BCF,
△CDG,△ADH分别为以 AB,BC,CD,DA为底边的等腰三角形,
沿虚线剪开后,分别以 AB,BC,CD,DA为折痕折起△ABE,△BCF,
知不足者好学 2 耻下问者自满
(第 16 题)
△CDG,△ADH,使得 E,F,G,H重合,得到一个四棱锥.当该四棱锥的侧面积是底面
积的 2 倍时,四棱锥的外接球的体积为_______.
四、解答题:本题共 6 小题,共 70 分.解答应写出文字说明、证明过程或演算步骤.
17.(10 分)已知 a,b,c 是同一平面内的三个向量,其中 a=(1,2).
(1)若 c=(3 +1, -3),且 c∥a,求 的值;
(2)若 b=(1,m)(m<0),且 a+2b 与 a-2b 垂直,求 a 与 b 的夹角θ.
18.(12 分)某校在高三年级学生一次数学考试后,对 90 分以上(含 90 分)的成绩进行统
计,其频率分布直方图如图所示,若 130~140 分数段的人数为 2 人.
(1)请估计一下这组数据的平均数 M;
(2)现根据考试成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、
第五组)中任意选出两人,形成“帮扶学习小组”.若选出的两人成绩之差大于 20,则称这
两人为“黄金搭档组”,试求选出的两人为“黄金搭档组”的概率.
19.(12 分)如图,在四棱锥 A-BCDE中,BE∥CD,BE⊥BC,AB=AC,平面 BCDE⊥平
面 ABC,M为 BC的中点.
(1)若 N是线段 AE的中点,求证:MN∥平面 ACD;
(2)若 BE=1,BC=2,CD=3,求证:DE⊥平面 AME.
(第 18 题)
知不足者好学 3 耻下问者自满
20.(12 分)△ABC的内角 A,B,C的对边分别为 a,b,c,cos A+ 3 sin A=0,a= 2 7 ,
b= 2 3 .
(1)求 c;
(2)设 D为 BC边上一点,且 AD⊥AC,求△ABD的面积.
21.(12 分)乒乓球比赛规则规定:一局比赛,双方比分在 10 平前,一方连续发球 2 次
后,对方再连续发球 2 次,依次轮换.每次发球,胜方得 1 分,负方得 0 分.设在甲、乙的
比赛中,每次发球,发球方得 1 分的概率为 0.6,各次发球的胜负结果相互独立.甲、乙的
一局比赛中,甲先发球.
(1)求开始第 4 次发球时,甲、乙的比分为 1 比 2 的概率;
(2)求开始第 5 次发球时,甲得分领先的概率.
22.(12 分)如图,在直三棱柱 ABC-A1B1C1 中,AB⊥BC,AA1=AC=2,BC=1,E,F
分别为 A1 C1,BC的中点.
(1)求证:平面 ABE⊥平面 B1BCC1;
(2)求证:在棱 AC上存在一点 M,使得平面 C1FM∥平面 ABE;
(3)求三棱锥 E-ABC的体积.
(第 21 题
知不足者好学 4 耻下问者自满
高二年级秋季开学数学试题
参考答案
一、单项选择题 1.B.2.D.3.C.4.C.5.A.6.A.7.C.8.D.
二、多项选择题 9.BD. 10.CD.11.BCD.12.AB.
三、填空题
13 14 15 16 500 3π.154. . 10 . .6; . cm3 .
27
提示:如图,连接 OE,交 AB于点 I,设 E,F,G,H重合于点 P,正方形的边长为
x x
x(x>0),则 OI= ,IE=6- .
2 2
(第 16 题)
∵ 该四棱锥的侧面积是底面积的 2 倍,
x x
∴ 4× (6- )=2x2,解得 x=4.
2 2
设该四棱锥的外接球的球心为 Q,半径为 R,则 OC= 2 2 ,OP= 2 3 ,R2=( 2 3 -
5
R 2 500 3π) +( 2 2 )2,解得 R= .∴ 外接球的体积 V= cm3.3 27
四、解答题
17.解:(1)因为 c=(3 +1, -3),且 c∥a,所以(3 +1)×2-( -3)×1=0,
解得 =-1;--------------------------4 分
a+2b=(3, 2+2m),
(2) 由题意,可知 a 2b 1 2 2m -----------------------------6 分 - =(-, - ).
因为 a+2b 与 a-2b 垂直,
1 1
所以(a+2b)·(a-2b)=0,解得 m=- ,则 b=(1,- ),--------------9 分
2 2
知不足者好学 5 耻下问者自满
π
所以 a·b=0,于是θ= .-----------------------------------------10 分
2
18.解:(1)M=95×0.01×10+105×0.025×10+115×0.045×10+125×0.015×10+
135×0.005×10=113(分).-------------------------------3 分
(2)设 90~140 分之间的人数是 n,由 130~140 分数段的人数为 2 人,可知 0.005×10×n
=2,解得 n=40.---------------------------5 分
依题意,第一组共有 40×0.01×10=4(人),记作 A1,A2,A3,A4;第五组共有 2 人,
记作 B1,B2.从第一组和第五组中任意选出两人,样本空间为{(A1,A2),(A1,A3),(A1,
A4),(A1,B1),(A1,B2),(A2,A1),(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,
A1),(A3,A2),(A3,A4),(A3,B1),(A3,B2),(A4,A1),(A4,A2),(A4,A3),(A4,
B1),(A4,B2),(B1,A1),(B1,A2),(B1,A3),(B1,A4),(B1,B2),(B2,A1),(B2,
A2),(B2,A3),(B2,A4),(B2,B1)},共有 30 个等可能的样本点.--------10 分
用事件 A表示“选出的两人为‘黄金搭档组’”.若两人成绩之差大于 20,则两人分
8
别来自于第一组和第五组,共有 16 个样本点,故 P(A)= .--------12 分
15
19.解:(1)取 AB的中点 H,连接 MH,NH.∵ N是 AE的中点,∴NH∥BE.
又 BE∥CD,∴NH∥CD.又∵NH 平面 ACD,∴NH∥平面 ACD.
同理可证,MH∥平面 ACD.而 MH NH=H,
∴ 平面 MNH∥平面 ACD,
∴ MN∥平面 ACD.--------------------------5 分
(2)连接 AM,DM,EM,由 AB=AC,M为 BC的中点,得 AM⊥BC.
又平面 BCDE⊥平面 ABC,平面 BCDE 平面 ABC=BC,AM 平面 ABC,∴AM⊥平
面 BCDE,∴AM⊥DE.
1
在 Rt△EBM中,BE=1,BM= BC=1,∴EM= .
2 2
1
在 Rt△DCM中,CD=3,CM= BC=1,∴DM= 10 .2
在直角梯形 BCDE中,可得 DE= (CD-BE)2+BC 2 = 2 2 ,
(第 18 题)
∴ EM 2+ DE 2 =DM 2 ,∴EM⊥DE.
又∵AM EM=M,∴ DE⊥平面 AME.-------------------12 分
5π
120 3.解:(1)由已知可得 tan A=- ,所以 A= .
3 6
知不足者好学 6 耻下问者自满
5π
在△ABC中,由余弦定理得 28=12+c2- 4 3 ccos ,即 c2+6c-16=0,6
解得 c=-8(舍去),c=2.--------6 分
π π
(2)由题设可得∠CAD= ,所以∠BAD=∠BAC-∠CAD= .
2 3
1
S ACgADVACD 2 1 5π
故 S = 1 π =2.又 S△ABC= ×2× 2 3 sin = 3 ,VABD ABgADgsin 2 6
2 3
3
所以 S△ABD= .-------------------------12 分3
21.解:用事件 Ai表示“第 1 次和第 2 次这两次发球,甲共得 i分”,i=0,1,2;Bi
表示“第 3 次和第 4 次这两次发球,甲共得 i分”,i=0,1,2;A表示“第 3 次发球,甲
得 1 分”;B表示“开始第 4 次发球时,甲、乙的比分为 1 比 2”;C=“开始第 5 次发球
时,甲得分领先”---------------------2 分.
(1)因为 P(A)=0.4,P(A0)=0.42=0.16,P(A1)=2×0.6×0.4=0.48,B=A0A+ A1A,
所以 P(B)=P(A0A+ A1A )=P(A0A)+P( A1A )=P(A0)P(A)+P(A1)P( A )=0.352.---6 分
(2)因为 P(B0)=0.62=0.36,P(B1)=2×0.4×0.6=0.48,P(B2)=0.42=0.16,
P(A2)=0.62=0.36.C=A1B2+A2B1+A2B2,
所以 P(C)=P(A1B2+A2B1+A2B2)=P(A1B2)+P(A2B1)+P(A2B2)
=P(A1)P(B2)+P(A2)P(B1)+P(A2)P(B2)=0.307 2.-----------------------12 分
22.解:(1)在直三棱柱 ABC-A1B1C1中,∵BB1⊥平面 ABC,
23.∴BB1⊥AB.
又∵AB⊥BC,BC BB1=B,
∴AB⊥平面 B1BCC1.
∴平面 ABE⊥平面 B1BCC1.--4 分
(3) 取 AC中点 M,连接 C1M,FM,
(4) ∵F为 BC的中点,∴FM∥AB.
∵AB 平面 ABE,FM 平面 ABE,∴ FM∥平面 ABE.
∵AM∥C1M,AM=C1M,
∴四边形 AMC1E为平行四边形.
∴C1M∥AE,C1M 平面 ABE.
(第 21 题)
知不足者好学 7 耻下问者自满
∴C1M∥平面 ABE.
∵C1M FM=M,
∴平面 C1FM∥平面 ABE,
即存在 AC的中点 M使得平面 C1FM∥平面 ABE.---------9 分
(3)点 E到底面的距离即为侧棱长 AA1=2.
∵在 Rt△ABC中,AC=2,BC=1,AB⊥BC,
S 1 3∴ AB= 3 , ABC= ABgBC= .2 2
V 3∴ E ABC= .-----------------------12 分3
知不足者好学 8 耻下问者自满
同课章节目录
