1.6 有理数的乘方(1) 课件(共27张PPT)
文档属性
| 名称 | 1.6 有理数的乘方(1) 课件(共27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-08 19:28:09 | ||
图片预览






文档简介
(共27张PPT)
沪科版 七年级上册
1.6 有理数的乘方(1)
教学目标
(1)正确理解乘方、幂、指数、底数等概念.通过对乘方意义的理解,培养学生观察、比较、分析、归纳、概括的能力,渗透转化思想.
(2)会进行有理数乘方的运算.
教学重点:幂底数指数的概念及其表示理解有理数乘法运算与乘方运算的联系.
教学难点:有理数的乘方的符号法则.
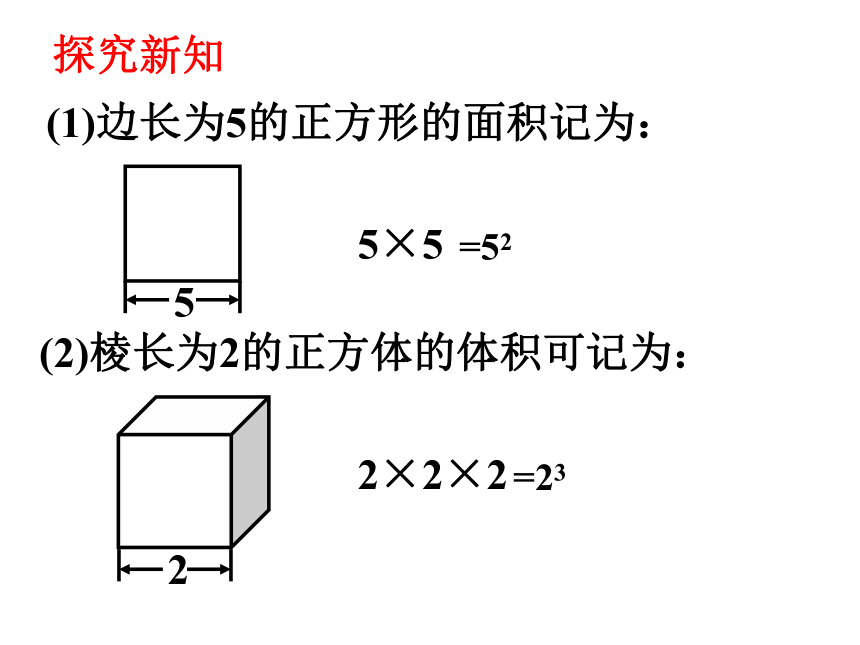
(1)边长为5的正方形的面积记为:
(2)棱长为2的正方体的体积可记为:
5×5
2×2×2
5
2
=52
=23
探究新知
5×5
=52
2×2×2
=23
那么4个 2 相乘可记为:
2个 5 相乘可记为:
3个 2 相乘可记为:
2×2×2×2=
24
那么n个 2 相乘可记为:
2×2×2
×······×2=
n个2
=2n
5×5记作52,
读作
(或5的二次方).
5的平方,
2×2×2
记作23,
读作
(或2的三次方).
2的立方,
2×2×2×2记作
24,
读作
2的4次方.
2×2×2
×······×2记作
n个2
2n,
读作
2的n次方.
记作25
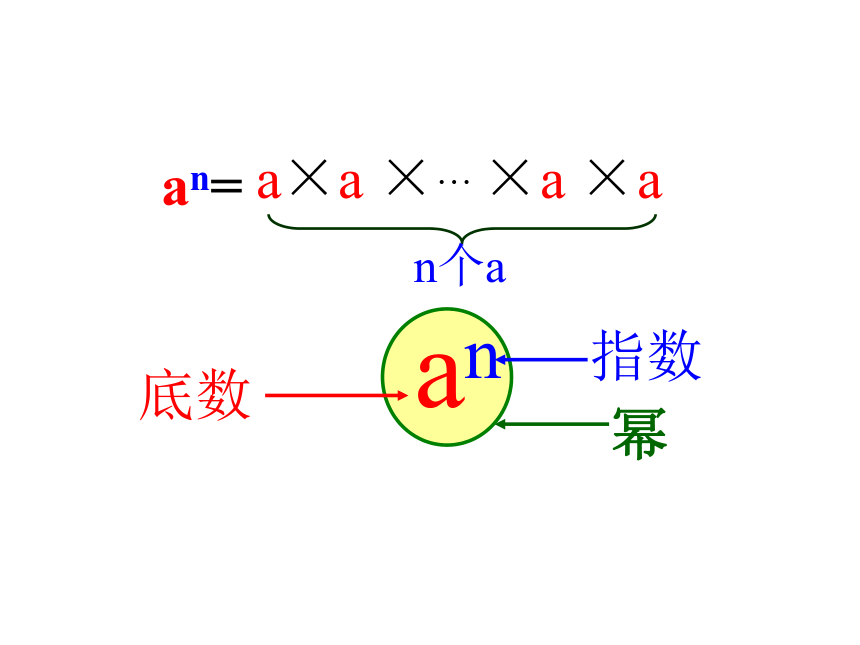
a×a ×… ×a ×a
n个a
求n个相同因数a的积的运算叫做乘方.
有理数的乘方
记作
an
2 ×2 ×2×2 ×2
5个2
an
底数
指数
幂
a×a ×… ×a ×a
n个a
an=
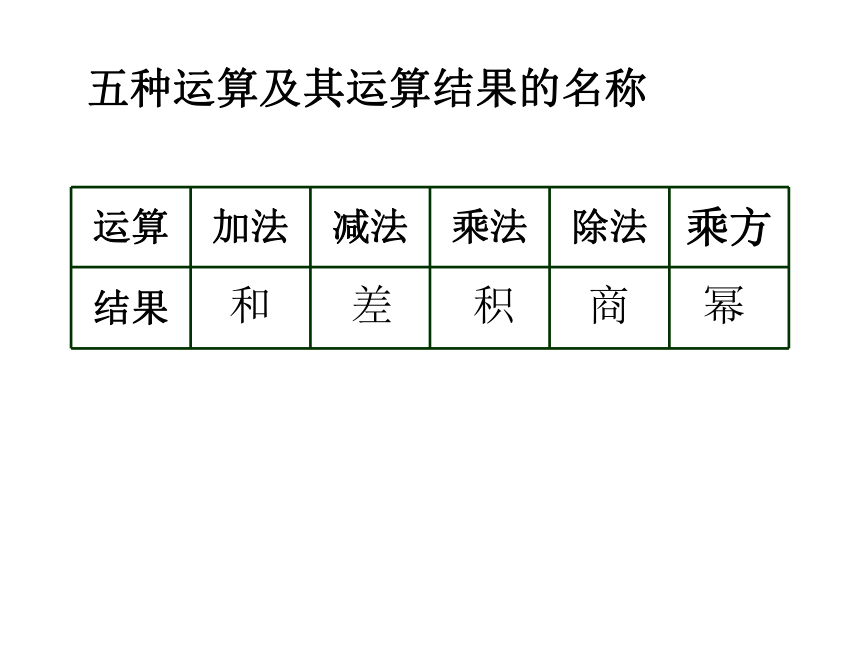
运算 加法 减法 乘法 除法 乘方
结果
幂
和
差
积
商
五种运算及其运算结果的名称
(1)在74中,底数是 ,指数是 ,
读作 ,或读作 ;
(2)在(-2)3中,底数是 ,指数是 ,
读作 ,或读作 .
7
4
7的4次方
7的4次幂
-2
3
-2的3次方
-2的3次幂
认识新知
(3)在 中,底数是 ,指数是 ,
读作 ,或读作 ;
(4)整数6可以看作底数是 指数是 的幂.
5
6
1
(- )5
1
2
-
1
2
的5次方
-
1
2
的5次幂
-
1
2
(1) 分数的乘方,在书写的时候一定要把整个分数用小括号括起来;
(2) 单独一个数可以看成是这个数本身的一次方,但是指数1我们通常省略不写.
例1 计算:
解:
(-4)×(-4)×(-4)
(-2)×(-2)×(-2)×(-2)
=-64
=16
(1)(-4)3 ;
(2)(-2)4 =
(1)(-4)3 =
(2)(-2)4 .
计算:
(1) (-1.5)2 ;
(2) 4× (-2)3;
(3) -(-2)4;
(4) (-2)3× (-2)2.
练习巩固
计算:
(1) (-1.5)2
(2) 4× (-2)3
(3) -(-2)4
(4) (-2)3× (-2)2
=(-1.5)×(-1.5)
=2.25
=4 ×(-2)×(-2)×(-2)
=4×(-8)
=-32
=-
16
=-8
×4
=-32
-34读作:
(1) -34与(-3)4的区别在哪里?
(-3)4读作:
34的相反数,
-3的四次方;
-81,
(-3)4=
81.
-34=
负数的乘方,在书写时一定要把整个负数(连同符号),用小括号括起来.这也是辨认底数的方法.
例2 计算:
(2) (- )×(- )2 +(- )÷[(- )3- ].
3
8
1
2
9
5
1
4
(1) -10+8÷ (-2)2-(-4)× (-2);
5
3
先算乘方,再算乘除,最后算加减;同级运算从左往右依次计算,如有括号,先算括号内的.
混合运算的顺序
例2 计算:
(2) (- )×(- )2 +(- )÷[(- )3- ].
3
8
1
2
9
5
1
4
(1) -10+8÷ (-2)2-(-4)× (-3);
5
3
解:
(1) -10+8÷ (-2)2-(-4)× (-3)
= -10+8÷4-(-4)× (-3)
= -10+
2
-
12
=-
20
例2 计算:
(2) (- )×(- )2 +(- )÷[(- )3- ].
3
8
1
2
9
5
1
4
(1) -10+8÷ (-2)2-(-4)× (-2);
5
3
解:
(2) (- )×(- )2 +(- )÷[(- )3- ]
3
8
1
2
9
5
1
4
5
3
=(- )× +(- )÷[- - ].
3
8
1
8
9
5
1
4
25
9
=-5
+
(- )÷(- )
3
8
3
8
=-5
+
1
=-4
例2 计算:
(2) (- )×(- )2 +(- )÷[(- )3- ].
3
8
1
2
9
5
1
4
(1) -10+8÷ (-2)2-(-4)× (-3);
5
3
解:
(1) 原式=
-10+8÷4-(-4)× (-3)
= -10+
2
-
12
=-
20
计算:
(1) -23-3× (-1)3 -(-1)4;
解:
(1) 原式=
-8
-3×(-1)
-1
=-8
-(-3)
-1
=-8
+
3
-1
=-6
练习巩固
计算:
(2) (-2)3 ÷ × (- )2 .
2
3
4
9
解:
(2) 原式=
-8
÷ ×
4
9
4
9
=-8
×
9
4
×
4
9
=-8
课堂小结
1.本节课我们学习了哪些内容?
2.你有什么收获 ?
3.你还有什么困惑?
1.(1)(-1)12底数是 ,指数是 .
(2)(-3)11表示 个 相乘.
(3)(-1)2022=__;
(-1)2023=__;
(-1)2n= __(n为正整数);
(-1)2n+1= (n为正整数).
(4)(+1)199 - (-1)200=___.
(5)-14+1=_____.
-1
12
11
-3
1
-1
1
-1
0
0
不计算下列各式的值,你能确定其符号吗?
你能得到什么规律吗?说出你的根据.
(1)(-1)51 ;(2)(-1)50; (3)150;
(4)151; (5)02 021 ; (6)12 022.
归纳:
(1)正数的任何次幂是正数;
(2)负数的偶次幂是正数;负数的奇次幂是负数;
(3)0的正整数次幂等于零;
(4)1的任何次幂等于1.
请同学们拿出准备好的纸:
进行对折、再对折……并作记录(两人合作)
问题:(1)对折一次有几层?
(2)对折二次有几层?
(3)对折三次有几层?
(4)对折四次有几层?
(5)一直对折下去,你会发现什么?
(若这张纸够大,可以折叠多少次)
学生自己操作,观察、发现、交流
猜想:对折二十次有几层?
对折n次有几层?
交流、探索
今天作业
课本P43习题1.6第1题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 七年级上册
1.6 有理数的乘方(1)
教学目标
(1)正确理解乘方、幂、指数、底数等概念.通过对乘方意义的理解,培养学生观察、比较、分析、归纳、概括的能力,渗透转化思想.
(2)会进行有理数乘方的运算.
教学重点:幂底数指数的概念及其表示理解有理数乘法运算与乘方运算的联系.
教学难点:有理数的乘方的符号法则.
(1)边长为5的正方形的面积记为:
(2)棱长为2的正方体的体积可记为:
5×5
2×2×2
5
2
=52
=23
探究新知
5×5
=52
2×2×2
=23
那么4个 2 相乘可记为:
2个 5 相乘可记为:
3个 2 相乘可记为:
2×2×2×2=
24
那么n个 2 相乘可记为:
2×2×2
×······×2=
n个2
=2n
5×5记作52,
读作
(或5的二次方).
5的平方,
2×2×2
记作23,
读作
(或2的三次方).
2的立方,
2×2×2×2记作
24,
读作
2的4次方.
2×2×2
×······×2记作
n个2
2n,
读作
2的n次方.
记作25
a×a ×… ×a ×a
n个a
求n个相同因数a的积的运算叫做乘方.
有理数的乘方
记作
an
2 ×2 ×2×2 ×2
5个2
an
底数
指数
幂
a×a ×… ×a ×a
n个a
an=
运算 加法 减法 乘法 除法 乘方
结果
幂
和
差
积
商
五种运算及其运算结果的名称
(1)在74中,底数是 ,指数是 ,
读作 ,或读作 ;
(2)在(-2)3中,底数是 ,指数是 ,
读作 ,或读作 .
7
4
7的4次方
7的4次幂
-2
3
-2的3次方
-2的3次幂
认识新知
(3)在 中,底数是 ,指数是 ,
读作 ,或读作 ;
(4)整数6可以看作底数是 指数是 的幂.
5
6
1
(- )5
1
2
-
1
2
的5次方
-
1
2
的5次幂
-
1
2
(1) 分数的乘方,在书写的时候一定要把整个分数用小括号括起来;
(2) 单独一个数可以看成是这个数本身的一次方,但是指数1我们通常省略不写.
例1 计算:
解:
(-4)×(-4)×(-4)
(-2)×(-2)×(-2)×(-2)
=-64
=16
(1)(-4)3 ;
(2)(-2)4 =
(1)(-4)3 =
(2)(-2)4 .
计算:
(1) (-1.5)2 ;
(2) 4× (-2)3;
(3) -(-2)4;
(4) (-2)3× (-2)2.
练习巩固
计算:
(1) (-1.5)2
(2) 4× (-2)3
(3) -(-2)4
(4) (-2)3× (-2)2
=(-1.5)×(-1.5)
=2.25
=4 ×(-2)×(-2)×(-2)
=4×(-8)
=-32
=-
16
=-8
×4
=-32
-34读作:
(1) -34与(-3)4的区别在哪里?
(-3)4读作:
34的相反数,
-3的四次方;
-81,
(-3)4=
81.
-34=
负数的乘方,在书写时一定要把整个负数(连同符号),用小括号括起来.这也是辨认底数的方法.
例2 计算:
(2) (- )×(- )2 +(- )÷[(- )3- ].
3
8
1
2
9
5
1
4
(1) -10+8÷ (-2)2-(-4)× (-2);
5
3
先算乘方,再算乘除,最后算加减;同级运算从左往右依次计算,如有括号,先算括号内的.
混合运算的顺序
例2 计算:
(2) (- )×(- )2 +(- )÷[(- )3- ].
3
8
1
2
9
5
1
4
(1) -10+8÷ (-2)2-(-4)× (-3);
5
3
解:
(1) -10+8÷ (-2)2-(-4)× (-3)
= -10+8÷4-(-4)× (-3)
= -10+
2
-
12
=-
20
例2 计算:
(2) (- )×(- )2 +(- )÷[(- )3- ].
3
8
1
2
9
5
1
4
(1) -10+8÷ (-2)2-(-4)× (-2);
5
3
解:
(2) (- )×(- )2 +(- )÷[(- )3- ]
3
8
1
2
9
5
1
4
5
3
=(- )× +(- )÷[- - ].
3
8
1
8
9
5
1
4
25
9
=-5
+
(- )÷(- )
3
8
3
8
=-5
+
1
=-4
例2 计算:
(2) (- )×(- )2 +(- )÷[(- )3- ].
3
8
1
2
9
5
1
4
(1) -10+8÷ (-2)2-(-4)× (-3);
5
3
解:
(1) 原式=
-10+8÷4-(-4)× (-3)
= -10+
2
-
12
=-
20
计算:
(1) -23-3× (-1)3 -(-1)4;
解:
(1) 原式=
-8
-3×(-1)
-1
=-8
-(-3)
-1
=-8
+
3
-1
=-6
练习巩固
计算:
(2) (-2)3 ÷ × (- )2 .
2
3
4
9
解:
(2) 原式=
-8
÷ ×
4
9
4
9
=-8
×
9
4
×
4
9
=-8
课堂小结
1.本节课我们学习了哪些内容?
2.你有什么收获 ?
3.你还有什么困惑?
1.(1)(-1)12底数是 ,指数是 .
(2)(-3)11表示 个 相乘.
(3)(-1)2022=__;
(-1)2023=__;
(-1)2n= __(n为正整数);
(-1)2n+1= (n为正整数).
(4)(+1)199 - (-1)200=___.
(5)-14+1=_____.
-1
12
11
-3
1
-1
1
-1
0
0
不计算下列各式的值,你能确定其符号吗?
你能得到什么规律吗?说出你的根据.
(1)(-1)51 ;(2)(-1)50; (3)150;
(4)151; (5)02 021 ; (6)12 022.
归纳:
(1)正数的任何次幂是正数;
(2)负数的偶次幂是正数;负数的奇次幂是负数;
(3)0的正整数次幂等于零;
(4)1的任何次幂等于1.
请同学们拿出准备好的纸:
进行对折、再对折……并作记录(两人合作)
问题:(1)对折一次有几层?
(2)对折二次有几层?
(3)对折三次有几层?
(4)对折四次有几层?
(5)一直对折下去,你会发现什么?
(若这张纸够大,可以折叠多少次)
学生自己操作,观察、发现、交流
猜想:对折二十次有几层?
对折n次有几层?
交流、探索
今天作业
课本P43习题1.6第1题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
