基本不等式[下学期]
图片预览


文档简介
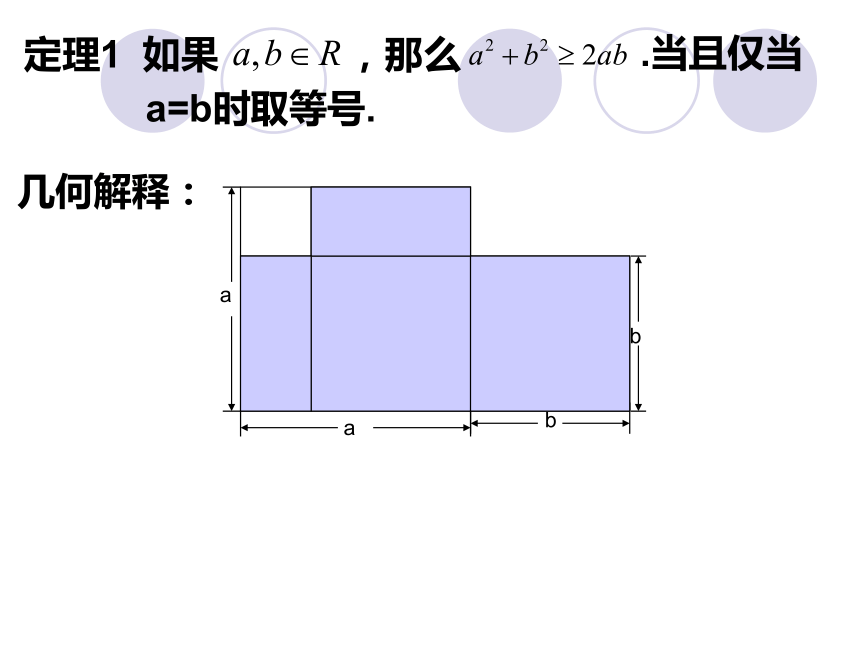
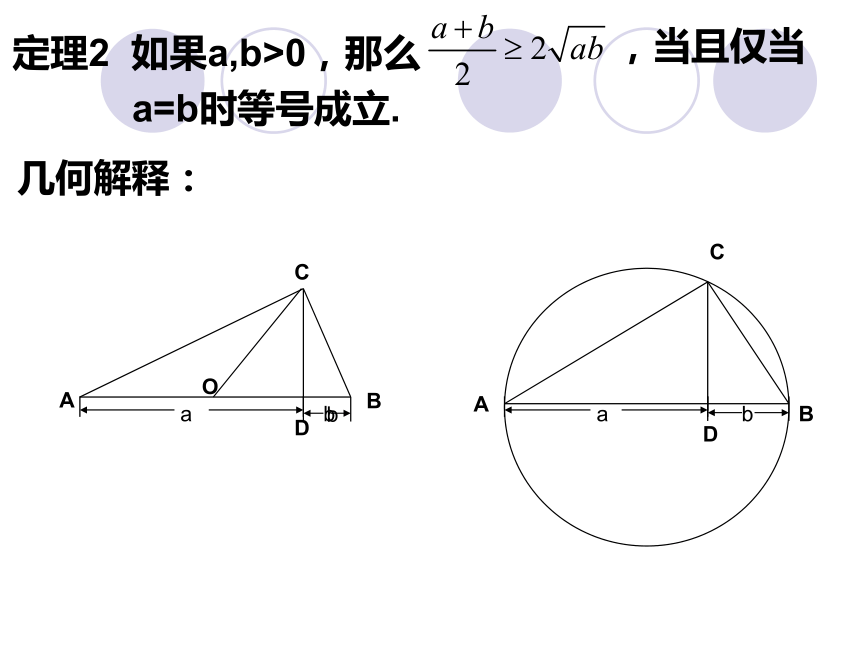
课件8张PPT。基本不等式定理1 如果 ,那么.当且仅当a=b时取等号.几何解释:定理2 如果a,b>0,那么,当且仅当a=b时等号成立.几何解释:例1 求证:
(1)所有周长相同的矩形中,正方形面积最大;
(2)在所有面积相同的矩形中,正方形周长最短.结论:设(1)若P时定值,当且仅当x=y时,S最小,为(2)若S为定值,当且仅当x=y时,P最大,为例2 已知x>1,y>1,且求的最值.引申:若条件改为呢?例3 求函数的最小值.变式:求函数的最小值.小结:用基本不等式需验证两个条件:(1)a,b是否满足都大于0(2)等号成立的条件.例3 设x>1,求函数的最小值.练习:设,求函数例4 设,且,求练习:已知且,a,b是常数,求x+y的最小值.例5 设且a+b+c=1,比较与8的大小.练习:设正数a,b,c,满足a+b+c=1,比较与5的大小.例4 某居民小区需要建一座八边形的休闲场所,它的主题造型平面图是由两个相同的矩形ABCD和EFGH构造成的面积为200平方米的十字型地域.计划在正方形MNPQ上建一座花坛,造价为每平方米4200元,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角上铺草坪,造价为每平方米80元.(1)设总造价为S元,AD长x元,试建立S关于x的函数关系式. (2)当x为何值时S最小,并求这个最小值.
(1)所有周长相同的矩形中,正方形面积最大;
(2)在所有面积相同的矩形中,正方形周长最短.结论:设(1)若P时定值,当且仅当x=y时,S最小,为(2)若S为定值,当且仅当x=y时,P最大,为例2 已知x>1,y>1,且求的最值.引申:若条件改为呢?例3 求函数的最小值.变式:求函数的最小值.小结:用基本不等式需验证两个条件:(1)a,b是否满足都大于0(2)等号成立的条件.例3 设x>1,求函数的最小值.练习:设,求函数例4 设,且,求练习:已知且,a,b是常数,求x+y的最小值.例5 设且a+b+c=1,比较与8的大小.练习:设正数a,b,c,满足a+b+c=1,比较与5的大小.例4 某居民小区需要建一座八边形的休闲场所,它的主题造型平面图是由两个相同的矩形ABCD和EFGH构造成的面积为200平方米的十字型地域.计划在正方形MNPQ上建一座花坛,造价为每平方米4200元,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角上铺草坪,造价为每平方米80元.(1)设总造价为S元,AD长x元,试建立S关于x的函数关系式. (2)当x为何值时S最小,并求这个最小值.
