基本不等式[上学期]
图片预览


文档简介
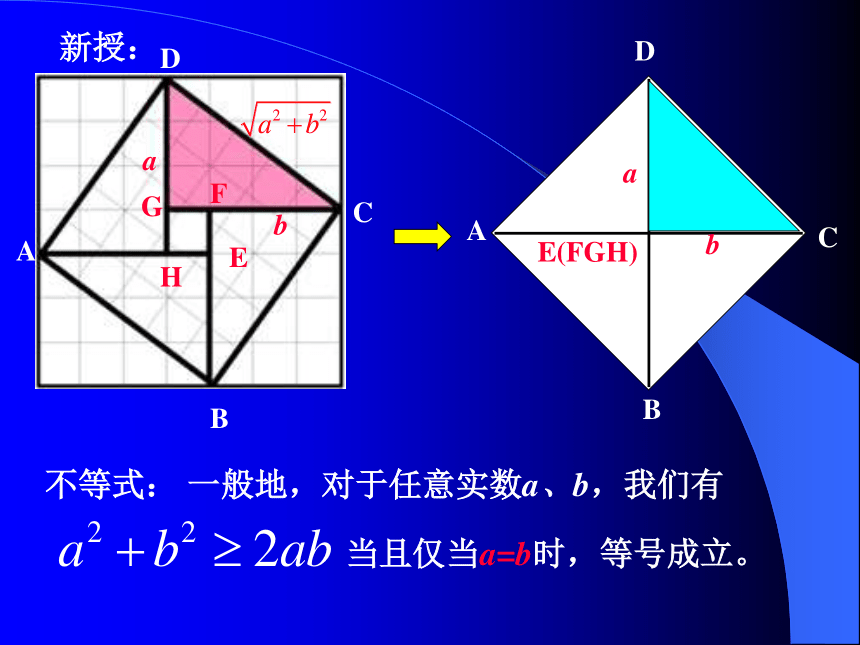
课件11张PPT。ICM2002会标新授:(1)(2)(3)B应用二:解决最大(小)值问题
例2、(1)用篱笆围一个面积为100m2的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短。最短篱笆是多少?
(2)一段长为36m的篱笆围成一矩形菜园,问这个矩形的长、宽各为多少时,菜园的面积最大。最大面积是多少?反思:由此题我们可以得到什么启示呢?定理:
(1)两个正数积为定值,和有最小值。
(2)两个正数和为定值,积有最大值。应用要点:
一正 二定 三相等21思考:当x<0时表达式又有何最值呢?小结: 1.两个正数的和为定值时,它们的积有最大值,即若a,b∈R+,且a+b=M,M为定值,
则ab≤ . 等号当且仅当a=b时成立. 2.两个正数的积为定值时,它们的和有最小值,即若a, b∈R+,且ab=P,P为定值,则 a+b≥2 , 等号当且仅当a=b时成立. 基本不等式的几何解释:半弦CD不大于半径小结:用均值不等式解决此类问题时,应按如下步骤进行:
(1)先理解题意,设变量,设变量时一般把要求最大值或最小值的变量定为函数;
(2)建立相应的函数关系式,把实际问题抽象为函数的最大值或最小值问题;
(3)在定义域内,求出函数的最大值或最小值;
(4)正确写出答案.
例2、(1)用篱笆围一个面积为100m2的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短。最短篱笆是多少?
(2)一段长为36m的篱笆围成一矩形菜园,问这个矩形的长、宽各为多少时,菜园的面积最大。最大面积是多少?反思:由此题我们可以得到什么启示呢?定理:
(1)两个正数积为定值,和有最小值。
(2)两个正数和为定值,积有最大值。应用要点:
一正 二定 三相等21思考:当x<0时表达式又有何最值呢?小结: 1.两个正数的和为定值时,它们的积有最大值,即若a,b∈R+,且a+b=M,M为定值,
则ab≤ . 等号当且仅当a=b时成立. 2.两个正数的积为定值时,它们的和有最小值,即若a, b∈R+,且ab=P,P为定值,则 a+b≥2 , 等号当且仅当a=b时成立. 基本不等式的几何解释:半弦CD不大于半径小结:用均值不等式解决此类问题时,应按如下步骤进行:
(1)先理解题意,设变量,设变量时一般把要求最大值或最小值的变量定为函数;
(2)建立相应的函数关系式,把实际问题抽象为函数的最大值或最小值问题;
(3)在定义域内,求出函数的最大值或最小值;
(4)正确写出答案.
