含绝对值不等式的解法高考题选讲[上学期]
文档属性
| 名称 | 含绝对值不等式的解法高考题选讲[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 126.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2005-09-26 00:00:00 | ||
图片预览




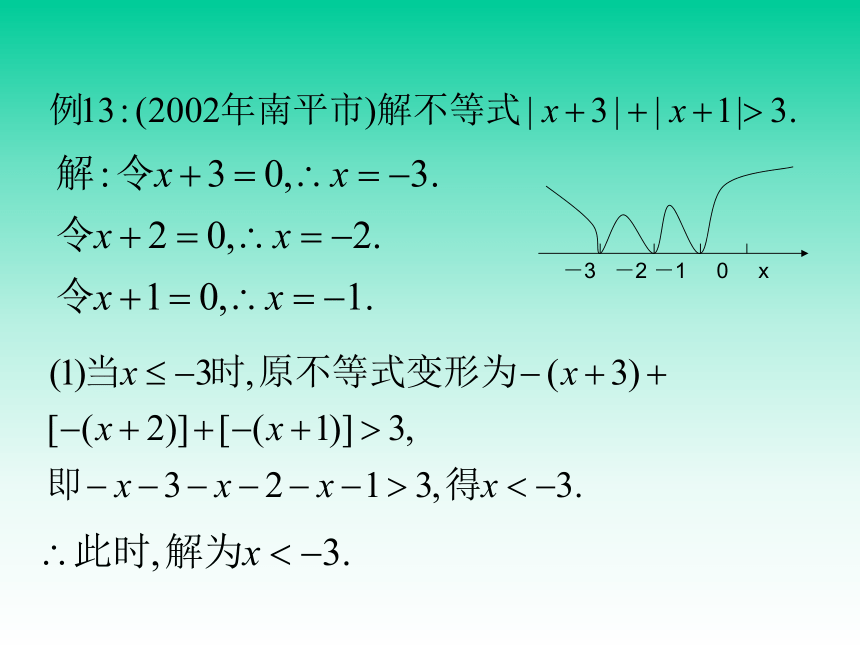




文档简介
课件28张PPT。绝对值不等式的解法授课教师: 谢大选四、含有多个绝对值(二个或二个以上)
等式问题.例12: (2000年武汉)解不等式|x -1| + |2 -x| >3 + x.解: 把原不等式变形为| X -1| + |X -2| > 3 + X.若| X -1| = 0,X = 1;若| X -2| = 0,X= 2.这样1,2把数轴分成了三部分,如图1-4-6所示.例14: 解下列不等式.历届高考试题解析与应注意的问题。( )知识联系与扩展例1:解不等式|ax+3|<2,a≠0.分析:本题属|ax+b|0)型不等式,可按此类不等式常规
方法来解,去掉绝对值符号后,还要注意到x的系数是参数a,
须对a分类讨论.解: 原不等式可化为-23.解:设y1=|2x-3|(y1≥0);y2 = 3.画其图象(如图所示),两图象的交点A和B的横坐标
(由方程|2x-3| = 3可以解得):x1 = 0,x2 = 3之外,即x<0,
或x>3,使不等式成立,故知原不等式的解集为{x|x<0,或
x>3} .例4: (2002年北京市·海淀区)若不等式|x + 1| + |x-1|的解集为非空数集,求实数m的取值范围.如图所示.令y2 = m,若y12.( )例6: (2000年杭州市)若不等式| x-4| + | 3-x|解集是空集,求a的取值范围.解法1: (1)当a≤0时,不等式|x-4| + |3-x|0时,先求不等式|x -4| + |3-x|值范围.①当x≥4时,x-4 + x-31.③当x≤3时,有4-x + 3-x1时,原不等式有解,从而当0原不等式解集为空集.
等式问题.例12: (2000年武汉)解不等式|x -1| + |2 -x| >3 + x.解: 把原不等式变形为| X -1| + |X -2| > 3 + X.若| X -1| = 0,X = 1;若| X -2| = 0,X= 2.这样1,2把数轴分成了三部分,如图1-4-6所示.例14: 解下列不等式.历届高考试题解析与应注意的问题。( )知识联系与扩展例1:解不等式|ax+3|<2,a≠0.分析:本题属|ax+b|
方法来解,去掉绝对值符号后,还要注意到x的系数是参数a,
须对a分类讨论.解: 原不等式可化为-2
(由方程|2x-3| = 3可以解得):x1 = 0,x2 = 3之外,即x<0,
或x>3,使不等式成立,故知原不等式的解集为{x|x<0,或
x>3} .例4: (2002年北京市·海淀区)若不等式|x + 1| + |x-1|
