选修4-4第四讲 柯西不等式(一)[下学期]
文档属性
| 名称 | 选修4-4第四讲 柯西不等式(一)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 63.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-28 00:00:00 | ||
图片预览








文档简介
课件21张PPT。第三讲
柯西不等式与排序不等式 二维形式的柯西不等式若a,b,c,d都是实数,则
(a2+b2)(c2+d2)≥(ac+bd)2
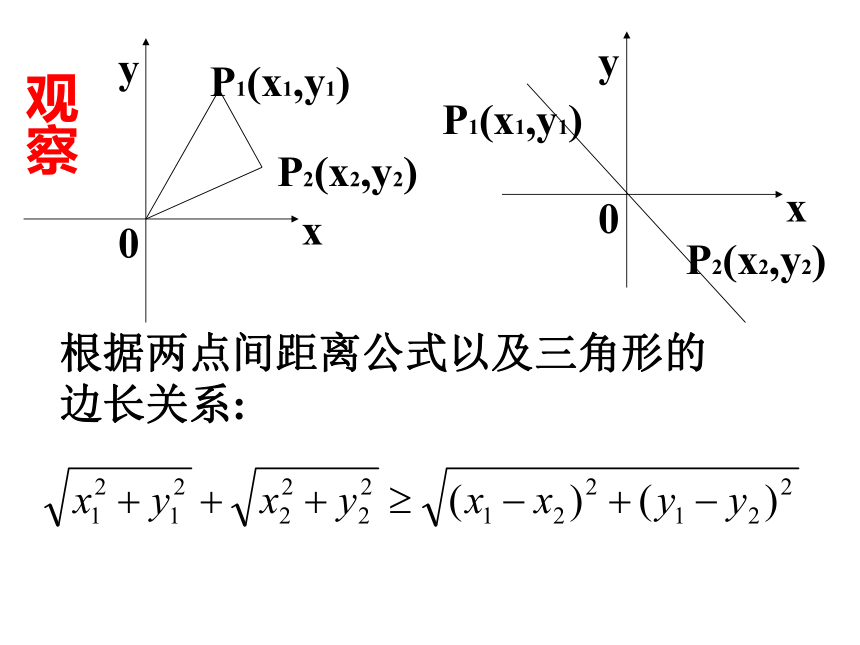
当且仅当ad=bc时,等号成立.定理1(二维形式的柯西不等式):你能证明吗?推论 向量形式:定理2: (柯西不等式的向量形式)根据两点间距离公式以及三角形的边长关系:观察定理3(二维形式的三角不等式)
设 ,那么 例题例1.已知a,b为实数,证明:
(a4+b4) (a2+b2)≥ (a3+b3)2例3.设a,b∈R+,a+b=1,求证
练习:作业第37页,第1,5,6题 一般形式的柯西不等式(a2+b2)(c2+d2)≥(ac+bd)2二维形式的柯西不等式):三维形式的柯西不等式):n维形式的柯西不等式):当且仅当 (i=1,2,…,n) 或 在一个 数k使得 (i=1,2,…,n) 时等号成立。
以上不等式称为一般形式的柯西不等式。一般形式的三角不等式例3 已知x+2y+3z=1,求
的最小值。 排序不等式
(a2+b2)(c2+d2)≥(ac+bd)2
当且仅当ad=bc时,等号成立.定理1(二维形式的柯西不等式):你能证明吗?推论 向量形式:定理2: (柯西不等式的向量形式)根据两点间距离公式以及三角形的边长关系:观察定理3(二维形式的三角不等式)
设 ,那么 例题例1.已知a,b为实数,证明:
(a4+b4) (a2+b2)≥ (a3+b3)2例3.设a,b∈R+,a+b=1,求证
练习:作业第37页,第1,5,6题 一般形式的柯西不等式(a2+b2)(c2+d2)≥(ac+bd)2二维形式的柯西不等式):三维形式的柯西不等式):n维形式的柯西不等式):当且仅当 (i=1,2,…,n) 或 在一个 数k使得 (i=1,2,…,n) 时等号成立。
以上不等式称为一般形式的柯西不等式。一般形式的三角不等式例3 已知x+2y+3z=1,求
的最小值。 排序不等式
