数学人教A版(2019)选择性必修第一册2.3.3点到直线的距离公式 课件(共32张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.3.3点到直线的距离公式 课件(共32张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 51.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-09 11:24:34 | ||
图片预览





文档简介
(共32张PPT)
2.3.3 点到直线的距离
——让“距离”的学习不再有距离
第二章 直线和圆的方程
2.3 直线的交点坐标与距离公式
如果你的目标是地平线
我愿为你搭建一条垂线段
利用点到直线的距离公式
计算出所需的路程最短
向着太阳出发吧,少年
我将在原点深情地目送你
成功到达理想的彼岸
1、两点间距离公式
2、坐标法
第一步:建立坐标系,用坐标表示有关的量。
第二步:进行有关代数运算
第三步:把代数运算结果翻译成几何关系。
特别地,点P(x,y)与坐标原点的距离是
旧知复习
x
y
O
P
Q
l
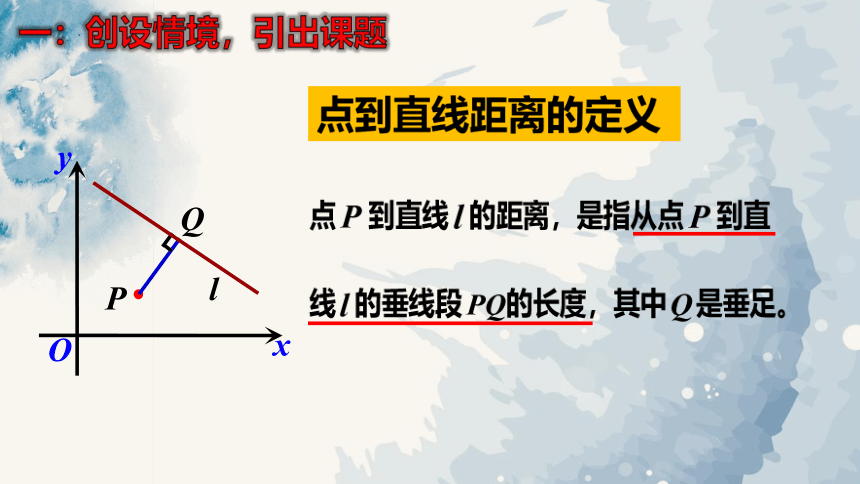
点到直线距离的定义
一:创设情境,引出课题
Q
P
l
x
y
O
M
N
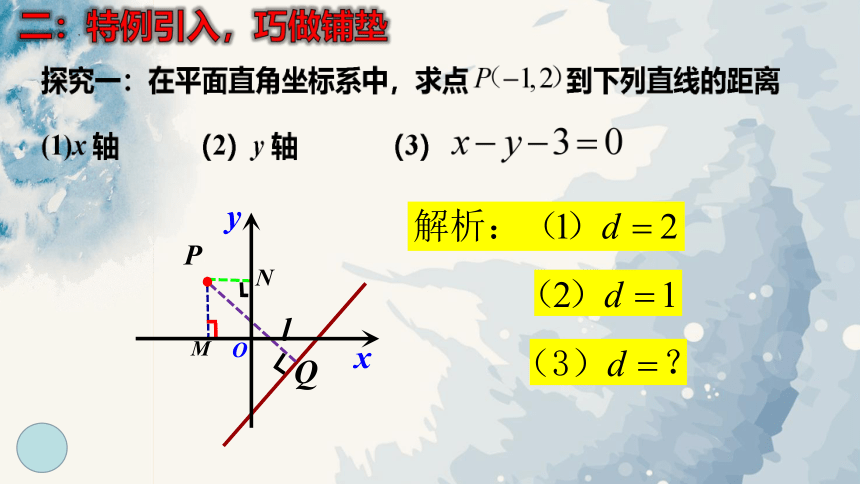
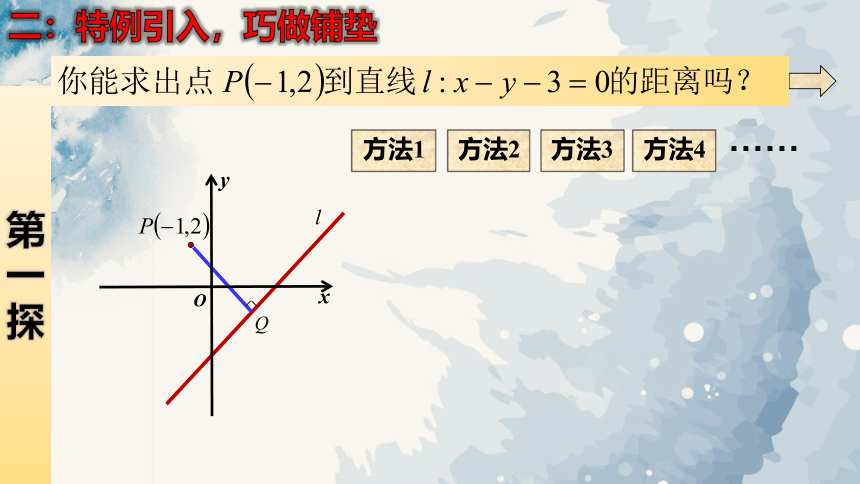
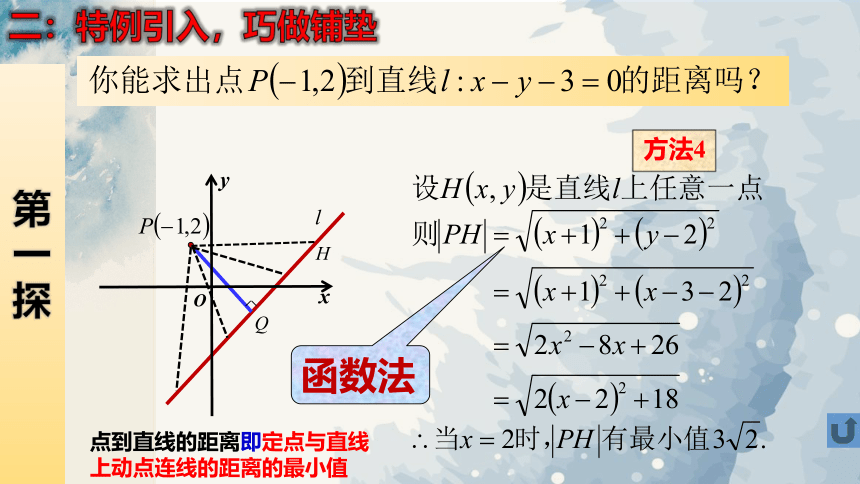
二:特例引入,巧做铺垫
第一探
……
方法1
方法2
方法3
方法4
x
y
O
二:特例引入,巧做铺垫
第一探
坐标法
方法1
x
y
O
二:特例引入,巧做铺垫
第一探
x
y
O
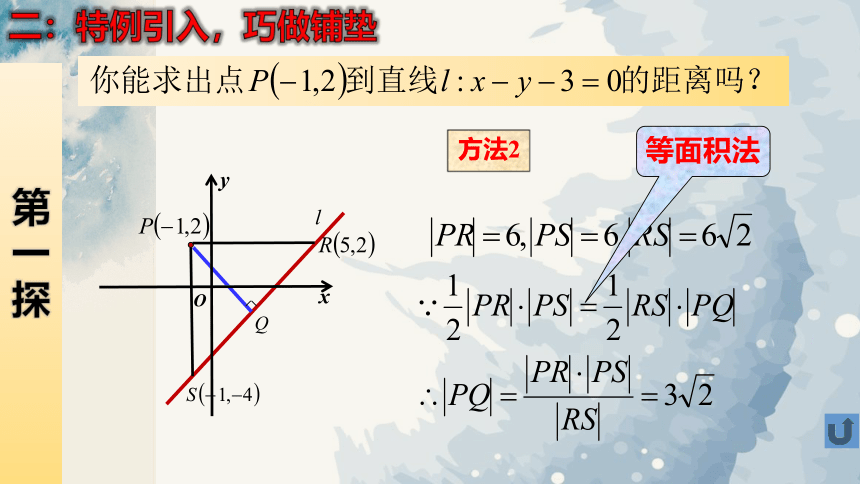
方法2
等面积法
二:特例引入,巧做铺垫
x
y
O
第一探
方法3
三角法
二:特例引入,巧做铺垫
第一探
方法4
x
y
O
函数法
二:特例引入,巧做铺垫
点到直线的距离即定点与直线上动点连线的距离的最小值
x
y
O
Q
P
l
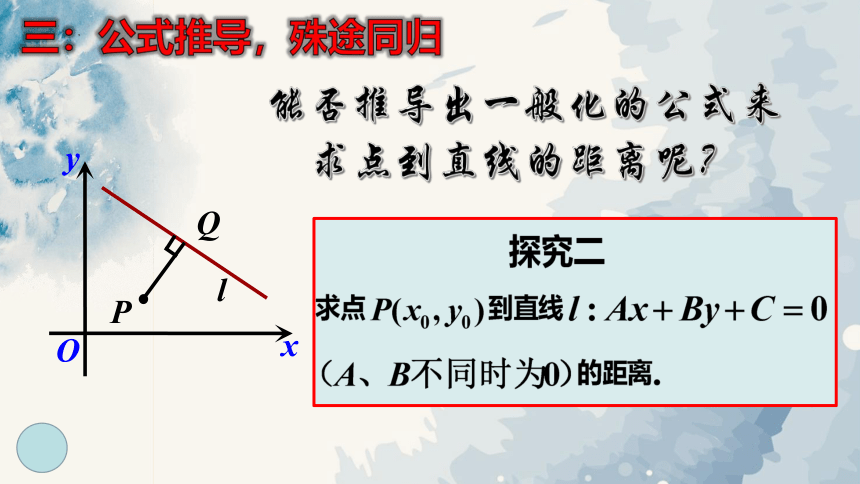
三:公式推导,殊途同归
能否推导出一般化的公式来
求点到直线的距离呢?
x
y
O
Q
P
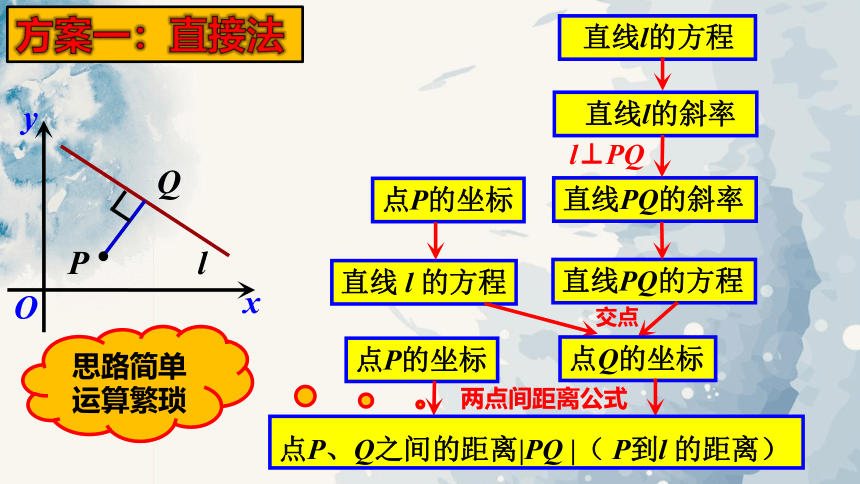
方案一:直接法
直线l的方程
直线 l 的方程
直线PQ的方程
交点
点P的坐标
直线PQ的斜率
点P的坐标
点Q的坐标
两点间距离公式
思路简单运算繁琐
直线l的斜率
l⊥PQ
点P、Q之间的距离|PQ |( P到l 的距离)
l
第二探
方案一:直接法
x
y
O
Q
x
y
O
Q
P
l
方案一:直接法
能否不求点Q的坐标?
(1)方法:根据点到直线距离的定义,将点到直线距离转化为
两点之间的距离。
(2)缺点:思路自然但运算量较大.
(3)思考:仔细观察求解过程, 思考引起复杂运算的原因是什么
(4)对策:由此能否给出简化运算的方法
方案一:直接法反思
解 密
追问:能否从方程组中直接求出 ?
在上述方法中,若设垂足 的坐标 ,则
结合方程组 我们能直接求出 ,进而
求出 .
Q
①
②
③
④
③式的平方+
④式的平方得:
方案一:直接法解疑
改进:用设而不求法推导
“整体代换”
“设而不求”
x
y
O
S
R
l
Q
P
面积法求出|PQ|
求出|PR|
求出|PS|
利用勾股定理求出|RS|
求出点R的坐标
求出点S的坐标
方案二:等面积法(精彩推证)
第二探
方案二:等面积法
x
y
O
S
R
l
Q
已知点P(x0,y0),直线l:Ax+By+C=0,如何求点P到直线l的距离?
思考:我们知道,向量是解决距离、角度问题的有力工具,能否用向量的方法求点到直线的距离?
M(x,y)
x
y
O
P
P1
P2
n
解:点P到直线l的距离,就是 的模
设是直线l上任意一点M(x,y),n是与直线l的方向向量垂直的单位向量,则 是 在n上的投影向量
思考:如何利用直线l的方程得到与l的方向向量垂直的单位向量n?
第三探
方案三:向量法
已知点P(x0,y0),直线l:Ax+By+C=0,如何求点P到直线l的距离?
M(x,y)
x
y
O
P
P1
P2
n
解:l的方向向量为m=(B,-A),与m垂直的向量为(A,B)
所以与l的方向向量垂直的单位向量n=
从而 ·n=(x-x0,y-y0)·
=
因为点M在直线上,所以Ax+By+C=0,所以Ax+By=-C,代入上式得
·n=
因此|PQ|= = ·n=
方案三:向量法
平面内一点P(x0,y0) 到直线Ax+By+C=0的距离公式:
分子是P点坐标代入直线方程左边
分母是直线未知数x、y系数平方和的算术根
四:探究归纳,展示成果
注意直线方程必须
是一般式
第四探
x
y
O
x
y
O
特殊情况,殊途同归
直线是特殊直线(与坐标轴垂直),也可以用数形结合求解.
注: A=0或B=0,此公式也成立,但当A=0或B=0时一般不用此公式计算距离.
点到直线的距离公式
点P(x0,y0) 到直线Ax+By+C=0(其中A,B不同时为0)的距离为
注: A=0或B=0,此公式也成立,但当A=0或B=0时一般不用此公式计算距离.
五:公式记忆,学以致用
解析:
解:设AB边上的高为h,则 ,
所以直线AB的方程为y-3=-(x-1), 即x+y-4=0
则点C到直线AB的距离为
故△ABC的面积为
例6:已知点A(1,3),B(3,1),C(-1,0),求△ABC的面积
x
y
O
D
E
A
B
C
h
还有其他方法吗?
五:公式记忆,学以致用
六:当堂检测,知识过手
已知直线l经过点M(-1,2),且A(2,3),B(-4,5)两点到直线l的距离相等,求直线l的方程.
典型例题
解:(方法一)当过点M(-1,2)的直线l的斜率不存在时,直线l的方程为x=-1,
恰好A(2,3),B(-4,5)两点到直线l的距离相等,故x=-1满足题意;
当过点M(-1,2)的直线l的斜率存在时,
设l的方程为y-2=k(x+1),即kx-y+k+2=0,
由A(2,3)与B(-4,5)两点到直线l的距离相等,得
即x+3y-5=0.
综上所述,直线l的方程为x=-1或x+3y-5=0.
已知直线l经过点M(-1,2),且A(2,3),B(-4,5)两点到直线l的距离相等,求直线l的方程.
典型例题
(方法二)由题意得l∥AB或l过AB的中点.
当l∥AB时,设直线AB的斜率为kAB,
即x+3y-5=0.
当l过AB的中点(-1,4)时,直线l的方程为x=-1.
综上所述,直线l的方程为x=-1或x+3y-5=0.
延伸探究 若将本题改为“已知直线l经过点M(-1,2),点A(2,3),B(-4,5)在l的同侧且到该直线l的距离相等”,则所求l的方程为 .
求经过点P(-3,5),且与原点距离等于3的直线l的方程
典型例题
解:当直线的斜率存在时,设所求直线方程为y-5=k(x+3),整理,
得kx-y+3k+5=0.
所以原点到该直线的距离d==3.
所以15k+8=0.所以k=-.故所求直线方程为y-5=-(x+3),
即8x+15y-51=0.
当直线的斜率不存在时,直线方程为x=-3也满足题意.故满足题意的直线l的方程为8x+15y-51=0或x=-3.
在根据距离确定直线方程时,易忽略直线斜率不存在的情况,避免这种错误的方法是当用点斜式或斜截式表示直线方程时,应首先考虑斜率不存在的情况是否符合题设条件,然后再求解.
总结升华
学会了…的知识
掌握了…的方法
体会了…的思想
在…方面有待加强
回顾学习活动形成自主反思
七:归纳总结,思维提升
学习了本节课,你有哪些收获?
七:归纳总结,思维提升
函数与方程
数形结合
分类与整合
化归与转化
特殊到一般
数学抽象
直观想象
数学建模
数学运算
逻辑推理
如果你的目标是地平线
我愿为你搭建一条垂线段
利用点到直线的距离公式
计算出所需的路程最短
向着太阳出发吧,少年
我将在原点深情地目送你
成功到达理想的彼岸
2.3.3 点到直线的距离
——让“距离”的学习不再有距离
第二章 直线和圆的方程
2.3 直线的交点坐标与距离公式
如果你的目标是地平线
我愿为你搭建一条垂线段
利用点到直线的距离公式
计算出所需的路程最短
向着太阳出发吧,少年
我将在原点深情地目送你
成功到达理想的彼岸
1、两点间距离公式
2、坐标法
第一步:建立坐标系,用坐标表示有关的量。
第二步:进行有关代数运算
第三步:把代数运算结果翻译成几何关系。
特别地,点P(x,y)与坐标原点的距离是
旧知复习
x
y
O
P
Q
l
点到直线距离的定义
一:创设情境,引出课题
Q
P
l
x
y
O
M
N
二:特例引入,巧做铺垫
第一探
……
方法1
方法2
方法3
方法4
x
y
O
二:特例引入,巧做铺垫
第一探
坐标法
方法1
x
y
O
二:特例引入,巧做铺垫
第一探
x
y
O
方法2
等面积法
二:特例引入,巧做铺垫
x
y
O
第一探
方法3
三角法
二:特例引入,巧做铺垫
第一探
方法4
x
y
O
函数法
二:特例引入,巧做铺垫
点到直线的距离即定点与直线上动点连线的距离的最小值
x
y
O
Q
P
l
三:公式推导,殊途同归
能否推导出一般化的公式来
求点到直线的距离呢?
x
y
O
Q
P
方案一:直接法
直线l的方程
直线 l 的方程
直线PQ的方程
交点
点P的坐标
直线PQ的斜率
点P的坐标
点Q的坐标
两点间距离公式
思路简单运算繁琐
直线l的斜率
l⊥PQ
点P、Q之间的距离|PQ |( P到l 的距离)
l
第二探
方案一:直接法
x
y
O
Q
x
y
O
Q
P
l
方案一:直接法
能否不求点Q的坐标?
(1)方法:根据点到直线距离的定义,将点到直线距离转化为
两点之间的距离。
(2)缺点:思路自然但运算量较大.
(3)思考:仔细观察求解过程, 思考引起复杂运算的原因是什么
(4)对策:由此能否给出简化运算的方法
方案一:直接法反思
解 密
追问:能否从方程组中直接求出 ?
在上述方法中,若设垂足 的坐标 ,则
结合方程组 我们能直接求出 ,进而
求出 .
Q
①
②
③
④
③式的平方+
④式的平方得:
方案一:直接法解疑
改进:用设而不求法推导
“整体代换”
“设而不求”
x
y
O
S
R
l
Q
P
面积法求出|PQ|
求出|PR|
求出|PS|
利用勾股定理求出|RS|
求出点R的坐标
求出点S的坐标
方案二:等面积法(精彩推证)
第二探
方案二:等面积法
x
y
O
S
R
l
Q
已知点P(x0,y0),直线l:Ax+By+C=0,如何求点P到直线l的距离?
思考:我们知道,向量是解决距离、角度问题的有力工具,能否用向量的方法求点到直线的距离?
M(x,y)
x
y
O
P
P1
P2
n
解:点P到直线l的距离,就是 的模
设是直线l上任意一点M(x,y),n是与直线l的方向向量垂直的单位向量,则 是 在n上的投影向量
思考:如何利用直线l的方程得到与l的方向向量垂直的单位向量n?
第三探
方案三:向量法
已知点P(x0,y0),直线l:Ax+By+C=0,如何求点P到直线l的距离?
M(x,y)
x
y
O
P
P1
P2
n
解:l的方向向量为m=(B,-A),与m垂直的向量为(A,B)
所以与l的方向向量垂直的单位向量n=
从而 ·n=(x-x0,y-y0)·
=
因为点M在直线上,所以Ax+By+C=0,所以Ax+By=-C,代入上式得
·n=
因此|PQ|= = ·n=
方案三:向量法
平面内一点P(x0,y0) 到直线Ax+By+C=0的距离公式:
分子是P点坐标代入直线方程左边
分母是直线未知数x、y系数平方和的算术根
四:探究归纳,展示成果
注意直线方程必须
是一般式
第四探
x
y
O
x
y
O
特殊情况,殊途同归
直线是特殊直线(与坐标轴垂直),也可以用数形结合求解.
注: A=0或B=0,此公式也成立,但当A=0或B=0时一般不用此公式计算距离.
点到直线的距离公式
点P(x0,y0) 到直线Ax+By+C=0(其中A,B不同时为0)的距离为
注: A=0或B=0,此公式也成立,但当A=0或B=0时一般不用此公式计算距离.
五:公式记忆,学以致用
解析:
解:设AB边上的高为h,则 ,
所以直线AB的方程为y-3=-(x-1), 即x+y-4=0
则点C到直线AB的距离为
故△ABC的面积为
例6:已知点A(1,3),B(3,1),C(-1,0),求△ABC的面积
x
y
O
D
E
A
B
C
h
还有其他方法吗?
五:公式记忆,学以致用
六:当堂检测,知识过手
已知直线l经过点M(-1,2),且A(2,3),B(-4,5)两点到直线l的距离相等,求直线l的方程.
典型例题
解:(方法一)当过点M(-1,2)的直线l的斜率不存在时,直线l的方程为x=-1,
恰好A(2,3),B(-4,5)两点到直线l的距离相等,故x=-1满足题意;
当过点M(-1,2)的直线l的斜率存在时,
设l的方程为y-2=k(x+1),即kx-y+k+2=0,
由A(2,3)与B(-4,5)两点到直线l的距离相等,得
即x+3y-5=0.
综上所述,直线l的方程为x=-1或x+3y-5=0.
已知直线l经过点M(-1,2),且A(2,3),B(-4,5)两点到直线l的距离相等,求直线l的方程.
典型例题
(方法二)由题意得l∥AB或l过AB的中点.
当l∥AB时,设直线AB的斜率为kAB,
即x+3y-5=0.
当l过AB的中点(-1,4)时,直线l的方程为x=-1.
综上所述,直线l的方程为x=-1或x+3y-5=0.
延伸探究 若将本题改为“已知直线l经过点M(-1,2),点A(2,3),B(-4,5)在l的同侧且到该直线l的距离相等”,则所求l的方程为 .
求经过点P(-3,5),且与原点距离等于3的直线l的方程
典型例题
解:当直线的斜率存在时,设所求直线方程为y-5=k(x+3),整理,
得kx-y+3k+5=0.
所以原点到该直线的距离d==3.
所以15k+8=0.所以k=-.故所求直线方程为y-5=-(x+3),
即8x+15y-51=0.
当直线的斜率不存在时,直线方程为x=-3也满足题意.故满足题意的直线l的方程为8x+15y-51=0或x=-3.
在根据距离确定直线方程时,易忽略直线斜率不存在的情况,避免这种错误的方法是当用点斜式或斜截式表示直线方程时,应首先考虑斜率不存在的情况是否符合题设条件,然后再求解.
总结升华
学会了…的知识
掌握了…的方法
体会了…的思想
在…方面有待加强
回顾学习活动形成自主反思
七:归纳总结,思维提升
学习了本节课,你有哪些收获?
七:归纳总结,思维提升
函数与方程
数形结合
分类与整合
化归与转化
特殊到一般
数学抽象
直观想象
数学建模
数学运算
逻辑推理
如果你的目标是地平线
我愿为你搭建一条垂线段
利用点到直线的距离公式
计算出所需的路程最短
向着太阳出发吧,少年
我将在原点深情地目送你
成功到达理想的彼岸
