人教版数学八年级上册 14.2.2完全平方公式 课件 (word,含答案)
文档属性
| 名称 | 人教版数学八年级上册 14.2.2完全平方公式 课件 (word,含答案) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-08 20:00:10 | ||
图片预览






文档简介
14.2.2 完全平方公式
第十四章 整式的乘法与因式分解
14.2 乘法公式
情境引入
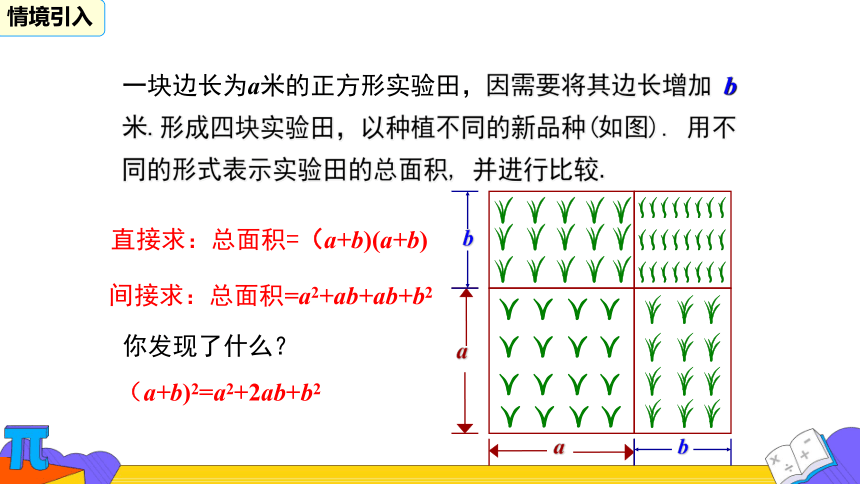
一块边长为a米的正方形实验田,因需要将其边长增加 b 米.形成四块实验田,以种植不同的新品种(如图). 用不同的形式表示实验田的总面积, 并进行比较.
a
a
b
b
直接求:总面积=(a+b)(a+b)
间接求:总面积=a2+ab+ab+b2
你发现了什么?
(a+b)2=a2+2ab+b2
复习引入
1
多项式与多项式相乘的法则是什么?
?
符号语言表示为:(????+????)????+????=????????+????????+????????+????????.
?
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
复习引入
2
乘法公式中的平方差公式是什么?
?
(????+????)?????????=????2?????2??.
?
两个数的和与这两个数的差的积,等于这两个数的
平方差.
公式中的 ????,???? 可以表示数或式子.
?
问题1 计算下列多项式的积,你能发现什么规律?
(1) (p+1)2=(p+1)(p+1)= .
p2+2p+1
(2) (m+2)2=(m+2)(m+2)= .
m2+4m+4
(3) (p-1)2=(p-1)(p-1)= .
p2-2p+1
(4) (m-2)2=(m-2)(m-2)= .
m2-4m+4
问题2 根据你发现的规律,你能写出下列式子的答案吗?
(a+b)2= .
a2+2ab+b2
(a-b)2= .
a2-2ab+b2
合作探究
探究新知
对任意的?????、????,上述发现的规律都成立吗?
?
∴
?
????+????2=????+????????+????,
?
=????2+????????+????????+????2,
?
=????2+2????????+????2,
?
????+????2=a2+2????????+????2.
?
∴
?
两个数的和的平方,等于这两个数的平方和,加上这两个数乘积的 2?倍.
?
探究新知
能用文字语言表述两数和的完全平方公式吗?
思考
两个数的和的平方,等于它们的平方和,加上它们的积的 2 倍.
?
公式中的 ????,?????可以表示数或式子.
?
两数和的完全平方公式:????+????2=????2+2????????+????2.
?
探究新知
能用下面图形的面积说明两数和的完全平方公式的几何意义吗?
(a+b)2
a2+2ab+b2 .
a2
ab
b2
ab
=
探究新知
能类比两数和的完全平方公式的学习过程,
表示两数差的完全平方吗?即:(a?b)2=?
法一:
(a?b)2=(a?b)(a?b)
=a2?ab?ab+b2
=a2?2ab+b2.
法二:
(a?b)2=[a+(?b)]2
=a2+2·a·(?b)+(?b)2
=a2?2ab+b2.
(a?b)2 = a2?2ab+b2.
探究新知
两个数的差的平方,等于它们的平方和,减去它们的积的 2 倍.
?
公式中的 ????,???? 可以表示数或式子.
?
两数差的完全平方公式:?????????2=????2?2????????+????2.
?
a2?2(a?b)b?b2.
探究新知
几何意义
(a?b)b
(a?b)2
b2
(a?b)b
(a?b)2
a2
a2?2ab+b2 .
=
探究新知
两数和的完全平方公式:????+????2=????2+2????????+????2.
?
两数差的完全平方公式:?????????2=????2?2????????+????2.
?
完全平方公式:????±????2=????2±2????????+????2.?
?
两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的 2 倍.
?
公式中的 ????,???? 可以表示数或式子.
?
典例精析
例1 运用完全平方公式计算:
解: (4m+n)2=
=16m2
(1)(4m+n)2;
(a +b)2= a2 + 2 ab + b2
(4m)2
+2?(4m) ?n
+n2
+8mn
+n2;
(a - b)2 = a2 - 2 ab + b2
y2
=y2
-y
+
解: =
+
-2?y?
(2)
利用完全平方公式计算:
(1)(5-a)2; (2)(-3m-4n)2;
(3)(-3a+b)2.
针对训练
(3)(-3a+b)2=9a2-6ab+b2.
解:(1)(5-a)2=25-10a+a2;
(2)(-3m-4n)2=9m2+24mn+16n2;
(1) 1022;
解: 1022
= (100+2)2
=10000+400+4
=10404.
(2) 992.
992
= (100 –1)2
=10000 -200+1
=9801.
例2 运用完全平方公式计算:
方法总结:运用完全平方公式进行简便计算,要熟记完全平方公式的特征,将原式转化为能利用完全平方公式的形式.
?????????2=????2?2????????+????2.
?
(a+????)2??=????2+2????????+????2,
?
符号语言:
文字叙述:
两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的?2?倍.
?
注意
课
堂
总
结
完全平方公式:
公式中的?????,???? 可以表示数或式子.
第十四章 整式的乘法与因式分解
14.2 乘法公式
情境引入
一块边长为a米的正方形实验田,因需要将其边长增加 b 米.形成四块实验田,以种植不同的新品种(如图). 用不同的形式表示实验田的总面积, 并进行比较.
a
a
b
b
直接求:总面积=(a+b)(a+b)
间接求:总面积=a2+ab+ab+b2
你发现了什么?
(a+b)2=a2+2ab+b2
复习引入
1
多项式与多项式相乘的法则是什么?
?
符号语言表示为:(????+????)????+????=????????+????????+????????+????????.
?
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
复习引入
2
乘法公式中的平方差公式是什么?
?
(????+????)?????????=????2?????2??.
?
两个数的和与这两个数的差的积,等于这两个数的
平方差.
公式中的 ????,???? 可以表示数或式子.
?
问题1 计算下列多项式的积,你能发现什么规律?
(1) (p+1)2=(p+1)(p+1)= .
p2+2p+1
(2) (m+2)2=(m+2)(m+2)= .
m2+4m+4
(3) (p-1)2=(p-1)(p-1)= .
p2-2p+1
(4) (m-2)2=(m-2)(m-2)= .
m2-4m+4
问题2 根据你发现的规律,你能写出下列式子的答案吗?
(a+b)2= .
a2+2ab+b2
(a-b)2= .
a2-2ab+b2
合作探究
探究新知
对任意的?????、????,上述发现的规律都成立吗?
?
∴
?
????+????2=????+????????+????,
?
=????2+????????+????????+????2,
?
=????2+2????????+????2,
?
????+????2=a2+2????????+????2.
?
∴
?
两个数的和的平方,等于这两个数的平方和,加上这两个数乘积的 2?倍.
?
探究新知
能用文字语言表述两数和的完全平方公式吗?
思考
两个数的和的平方,等于它们的平方和,加上它们的积的 2 倍.
?
公式中的 ????,?????可以表示数或式子.
?
两数和的完全平方公式:????+????2=????2+2????????+????2.
?
探究新知
能用下面图形的面积说明两数和的完全平方公式的几何意义吗?
(a+b)2
a2+2ab+b2 .
a2
ab
b2
ab
=
探究新知
能类比两数和的完全平方公式的学习过程,
表示两数差的完全平方吗?即:(a?b)2=?
法一:
(a?b)2=(a?b)(a?b)
=a2?ab?ab+b2
=a2?2ab+b2.
法二:
(a?b)2=[a+(?b)]2
=a2+2·a·(?b)+(?b)2
=a2?2ab+b2.
(a?b)2 = a2?2ab+b2.
探究新知
两个数的差的平方,等于它们的平方和,减去它们的积的 2 倍.
?
公式中的 ????,???? 可以表示数或式子.
?
两数差的完全平方公式:?????????2=????2?2????????+????2.
?
a2?2(a?b)b?b2.
探究新知
几何意义
(a?b)b
(a?b)2
b2
(a?b)b
(a?b)2
a2
a2?2ab+b2 .
=
探究新知
两数和的完全平方公式:????+????2=????2+2????????+????2.
?
两数差的完全平方公式:?????????2=????2?2????????+????2.
?
完全平方公式:????±????2=????2±2????????+????2.?
?
两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的 2 倍.
?
公式中的 ????,???? 可以表示数或式子.
?
典例精析
例1 运用完全平方公式计算:
解: (4m+n)2=
=16m2
(1)(4m+n)2;
(a +b)2= a2 + 2 ab + b2
(4m)2
+2?(4m) ?n
+n2
+8mn
+n2;
(a - b)2 = a2 - 2 ab + b2
y2
=y2
-y
+
解: =
+
-2?y?
(2)
利用完全平方公式计算:
(1)(5-a)2; (2)(-3m-4n)2;
(3)(-3a+b)2.
针对训练
(3)(-3a+b)2=9a2-6ab+b2.
解:(1)(5-a)2=25-10a+a2;
(2)(-3m-4n)2=9m2+24mn+16n2;
(1) 1022;
解: 1022
= (100+2)2
=10000+400+4
=10404.
(2) 992.
992
= (100 –1)2
=10000 -200+1
=9801.
例2 运用完全平方公式计算:
方法总结:运用完全平方公式进行简便计算,要熟记完全平方公式的特征,将原式转化为能利用完全平方公式的形式.
?????????2=????2?2????????+????2.
?
(a+????)2??=????2+2????????+????2,
?
符号语言:
文字叙述:
两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的?2?倍.
?
注意
课
堂
总
结
完全平方公式:
公式中的?????,???? 可以表示数或式子.
