1.2.2函数的表示法(第二课时)
文档属性
| 名称 | 1.2.2函数的表示法(第二课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 169.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-10 00:00:00 | ||
图片预览





文档简介
课件14张PPT。1.2.2 函数的表示法(第二课时) 1.常用的函数的三种表示法各自的优点:
1)列表法: 列出表格来表示两个变量的函数关系.
优点:
不需要计算,就可以直接看出与自变量相应的函数值.
2)图象法: 用函数图象表示两个变量之间的关系。
优点:
直观形象地表示随着自变量的变化,相应函数值变化的趋向 .
3)解析法:就是用数学表达式表示两个变量之间的对应关系.
优点: (1)简明、全面地概括了变量间的关系;
(2)可通过解析式求出每个自变量对应的函数值.知识回顾
思考 :
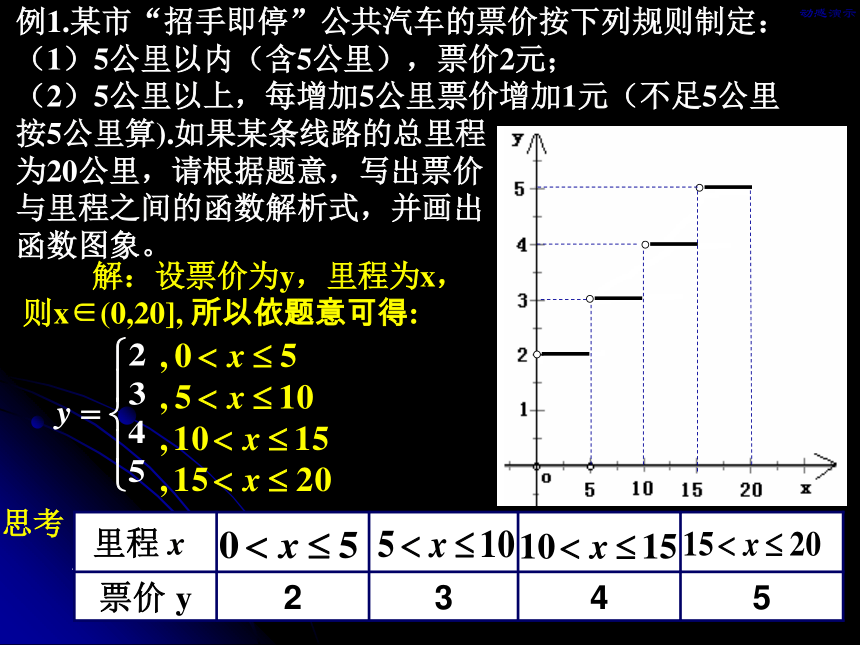
本题可否用列表法表示函数,如果可以,应怎样列表? 例1.某市“招手即停”公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里票价增加1元(不足5公里
按5公里算).如果某条线路的总里程
为20公里,请根据题意,写出票价
与里程之间的函数解析式,并画出
函数图象。 解:设票价为y,里程为x,
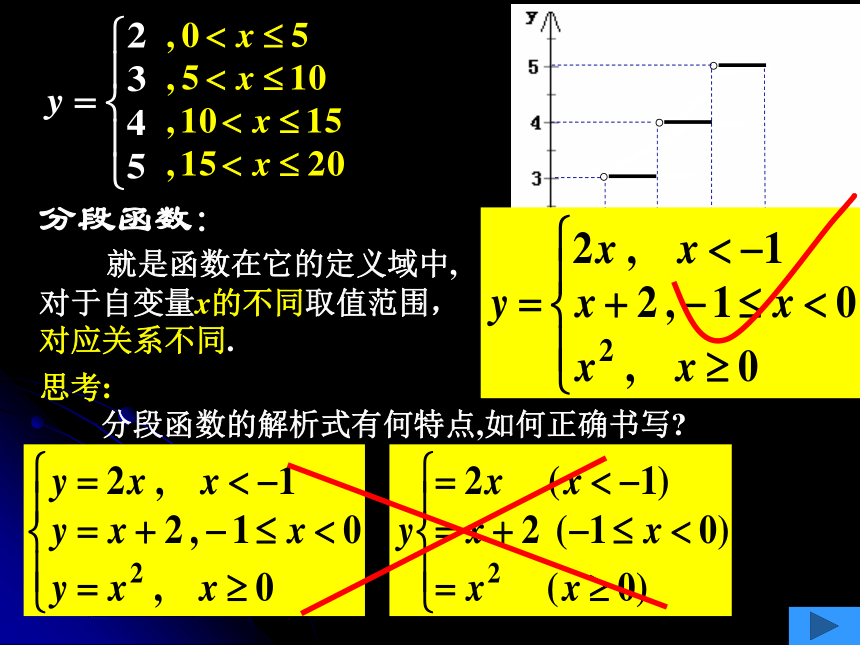
则x∈(0,20], 所以依题意可得:动感演示分段函数:
就是函数在它的定义域中,
对于自变量x的不同取值范围,
对应关系不同.思考:
分段函数的解析式有何特点,如何正确书写?分段函数
(1)有些函数在它的定义域中,对于自变量x的不同取值区间,对应关系也不同,这样的函数通常称为分段函数,分段函数是一个函数,而不是几个函数,其解析式是由几个不同的式子构成的,它们合为一个整体表示一个函数.
(2)画分段函数的图象时,一定要考虑区间端点是否包含在内,若端点包含在内,则用实点“·”表示,若端点不包含在内,则用空心点 “。” 表示.
(3)写分段函数定义域时,区间端点应不重不漏.
(4)处理分段函数问题时,要首先确定自变量的取值属于哪一个范围,然后选取相应的对应关系.
(5)求分段函数的定义域则是各段定义域的并集;求分段函数的值域也是分别求出各段上的值域后取并集;求分段函数最大(小)值则是分别在每段上求出最大(小)值,然后取各段中的最大(小)值.要点阐释“先内后外,逐层击破”的原则1、映射的概念 设A、B是两个非空集合,如果按照某种确定的对应关系f,使对于集合A中的任意一个元素x,在集合B中都有唯一确定的元素y与之对应,那么就称f: A→B为从集合A到集合B的一个映射. 比较函数的概念 映射
(1)映射f:A→B是由非空集合A、B以及A到B的对应关系f所确定的.
(2)映射定义中的两个集合A、B是非空的,可以是数集,也可以是点集或其他集合,A、B是有先后次序的,A到B的映射与B到A的映射一般是截然不同的,即f具有方向性.
(3)映射f:A→B要求:对于集合A中的任何一个元素在集合B中都有唯一的元素和它对应,这样有:
①A中每一个元素都可以在B中找到一个且只有一个元素和它对应.
②A中的不同元素允许对应B中的相同元素,即映射允许“多对一”、“一对一”,但不允许“一对多”.
③B中的元素允许A中无元素与之对应.
例题分析例2、以下给出的对应是不是从集合A到集合B的映射?(1)、集合A={P|P是数轴上的点},集合B=R
对应关系f:数轴上的点与它所代表的实数对应 (2)、集合A={P|P是平面直角坐标系中的点}
集合B={(x,y)|x∈R,y∈R}
对应关系f:平面直角坐标系中的点与它所
代表的实数对应(3)、集合A={x|x是三角形},集合B={x|x是圆}
对应关系f:每一个三角形都对应它的内切圆(4)、集合A={x|x是澄海中学的班级}
集合B={x|x是澄海中学的学生}
对应关系f:每一个班级对应班里的学生例题讲解:映射概念及应用
【例3】 判断下列对应是不是从集合A到集合B的映射:
(1)A=N*,B=N*,对应关系f:x→|x-3|;
(2)A={平面内的圆},B={平面内的矩形},对应关系f“作圆的内接矩形”;
(3)A={高一·一班的男生},B={男生的身高},对应关系f:每个男生对应自己的身高;
解:(1)由于A中元素3在对应关系f作用下其与3的差的绝对值为0,而0?B,故不是映射.
(2)因为一个圆有无数个内接矩形,即集合A中任何一个元素在集合B中有无数个元素与之对应,故不是映射.
(3)对A中任何一个元素,按照对应关系f,在B中都有唯一一个元素与之对应,符合映射定义,是映射.
点评:给定两集合A,B及对应关系f,判断是否是从集合A到集合B的映射,主要利用映射的定义,用通俗的语言讲:A→B的对应有“多对一”、“一对一”、“一对多”,前两种对应是A到B的映射,而最后一种不是A到B的映射.
例题分析例4、集合A={a ,b},集合B={c,d,e}(1)试建立一个由A到B的映射(2)由A到B的映射共有几个?结论:
若集合A中有m个元素,集合B有n个元素,
那么由A到B的映射共有nm个课堂小结1、分段函数的定义。
2、y =│f (x)│的图像的画法。
3、 通过本节课的学习,要理解映射的概念,能够
正确判断两个集合间的对应是否是映射。作业习题1.2 A组 10
1)列表法: 列出表格来表示两个变量的函数关系.
优点:
不需要计算,就可以直接看出与自变量相应的函数值.
2)图象法: 用函数图象表示两个变量之间的关系。
优点:
直观形象地表示随着自变量的变化,相应函数值变化的趋向 .
3)解析法:就是用数学表达式表示两个变量之间的对应关系.
优点: (1)简明、全面地概括了变量间的关系;
(2)可通过解析式求出每个自变量对应的函数值.知识回顾
思考 :
本题可否用列表法表示函数,如果可以,应怎样列表? 例1.某市“招手即停”公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里票价增加1元(不足5公里
按5公里算).如果某条线路的总里程
为20公里,请根据题意,写出票价
与里程之间的函数解析式,并画出
函数图象。 解:设票价为y,里程为x,
则x∈(0,20], 所以依题意可得:动感演示分段函数:
就是函数在它的定义域中,
对于自变量x的不同取值范围,
对应关系不同.思考:
分段函数的解析式有何特点,如何正确书写?分段函数
(1)有些函数在它的定义域中,对于自变量x的不同取值区间,对应关系也不同,这样的函数通常称为分段函数,分段函数是一个函数,而不是几个函数,其解析式是由几个不同的式子构成的,它们合为一个整体表示一个函数.
(2)画分段函数的图象时,一定要考虑区间端点是否包含在内,若端点包含在内,则用实点“·”表示,若端点不包含在内,则用空心点 “。” 表示.
(3)写分段函数定义域时,区间端点应不重不漏.
(4)处理分段函数问题时,要首先确定自变量的取值属于哪一个范围,然后选取相应的对应关系.
(5)求分段函数的定义域则是各段定义域的并集;求分段函数的值域也是分别求出各段上的值域后取并集;求分段函数最大(小)值则是分别在每段上求出最大(小)值,然后取各段中的最大(小)值.要点阐释“先内后外,逐层击破”的原则1、映射的概念 设A、B是两个非空集合,如果按照某种确定的对应关系f,使对于集合A中的任意一个元素x,在集合B中都有唯一确定的元素y与之对应,那么就称f: A→B为从集合A到集合B的一个映射. 比较函数的概念 映射
(1)映射f:A→B是由非空集合A、B以及A到B的对应关系f所确定的.
(2)映射定义中的两个集合A、B是非空的,可以是数集,也可以是点集或其他集合,A、B是有先后次序的,A到B的映射与B到A的映射一般是截然不同的,即f具有方向性.
(3)映射f:A→B要求:对于集合A中的任何一个元素在集合B中都有唯一的元素和它对应,这样有:
①A中每一个元素都可以在B中找到一个且只有一个元素和它对应.
②A中的不同元素允许对应B中的相同元素,即映射允许“多对一”、“一对一”,但不允许“一对多”.
③B中的元素允许A中无元素与之对应.
例题分析例2、以下给出的对应是不是从集合A到集合B的映射?(1)、集合A={P|P是数轴上的点},集合B=R
对应关系f:数轴上的点与它所代表的实数对应 (2)、集合A={P|P是平面直角坐标系中的点}
集合B={(x,y)|x∈R,y∈R}
对应关系f:平面直角坐标系中的点与它所
代表的实数对应(3)、集合A={x|x是三角形},集合B={x|x是圆}
对应关系f:每一个三角形都对应它的内切圆(4)、集合A={x|x是澄海中学的班级}
集合B={x|x是澄海中学的学生}
对应关系f:每一个班级对应班里的学生例题讲解:映射概念及应用
【例3】 判断下列对应是不是从集合A到集合B的映射:
(1)A=N*,B=N*,对应关系f:x→|x-3|;
(2)A={平面内的圆},B={平面内的矩形},对应关系f“作圆的内接矩形”;
(3)A={高一·一班的男生},B={男生的身高},对应关系f:每个男生对应自己的身高;
解:(1)由于A中元素3在对应关系f作用下其与3的差的绝对值为0,而0?B,故不是映射.
(2)因为一个圆有无数个内接矩形,即集合A中任何一个元素在集合B中有无数个元素与之对应,故不是映射.
(3)对A中任何一个元素,按照对应关系f,在B中都有唯一一个元素与之对应,符合映射定义,是映射.
点评:给定两集合A,B及对应关系f,判断是否是从集合A到集合B的映射,主要利用映射的定义,用通俗的语言讲:A→B的对应有“多对一”、“一对一”、“一对多”,前两种对应是A到B的映射,而最后一种不是A到B的映射.
例题分析例4、集合A={a ,b},集合B={c,d,e}(1)试建立一个由A到B的映射(2)由A到B的映射共有几个?结论:
若集合A中有m个元素,集合B有n个元素,
那么由A到B的映射共有nm个课堂小结1、分段函数的定义。
2、y =│f (x)│的图像的画法。
3、 通过本节课的学习,要理解映射的概念,能够
正确判断两个集合间的对应是否是映射。作业习题1.2 A组 10
