6.2.2 分层随机抽样 课件——2022-2023学年高一上学期数学北师大版(2019)必修第一册(共24张PPT)
文档属性
| 名称 | 6.2.2 分层随机抽样 课件——2022-2023学年高一上学期数学北师大版(2019)必修第一册(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-09 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
6.2.2 分层随机抽样
某电视台在互联网上就观众对某一节目的喜爱程度进行调查,参加调查的总人数为12 000人,其中持各种态度的人数分别为:很喜欢4 800人,喜欢3 600人,一般1 800人,不喜欢1 800人.电视台为进一步了解观众的具体想法和意见,打算从这12 000人中抽取60人进行更为详细的调查,应采取什么样的抽样方法呢
1.分层随机抽样的相关概念
【答案】小学生、初中生、高中生三个群体在年龄、体质等方面存在着明显的差异.
【问题情境】某市为调查中小学生的近视情况,在全市范围内分别对小学生、初中生、高中生三个群体抽样,进而了解中小学生的总体情况和三个群体近视情况的差异大小
【问题1】上述问题中总体有什么特征
【答案】抽取的样本可能集中于某一个群体,不具有代表性.
【问题2】若采用抽签法或随机数法抽样会出现什么结果
【问题3】为使抽取的样本更合理,更具有代表性,有更好的抽样方法解决该问题吗
【答案】有,可分不同群体抽取.
【问题4】层随机抽样的总体具有什么特性
【答案】分层随机抽样的总体按一个或多个变量划分成若干个子总体,并且每一个个体属于且仅属于一个子总体.
分层随机抽样的概念
将总体按其属性特征分成互不交叉的若干类型(有时称作层),然后在每个类型中按照所占比例随机抽取一定的个体,这种抽样方法通常叫作分层随机抽样.
特别提醒:分层随机抽样的特点
由于层与层之间有明显的区别,而层内个体间的差异不明显,所以在抽取样本时,一般在每层进行简单随机抽样,以保证公平、公正,在实际操作时,应先计算抽样比,然后计算每层需要抽取的个数:抽样比×该层个体数目=.
抽象概括
【例1】某学校有在职人员160人,其中行政人员有16人,教师有112人,后勤人员有32人.教育部门为了了解在职人员对学校机构改革的意见,要从中抽取一个容量为20的样本,请利用分层随机抽样的方法抽取,并写出抽样过程.
【解析】抽样过程如下:
第一步,确定抽样比,样本容量与总体容量的比为;
第二步,确定分别从三类人员中抽取的人数,从行政人员中抽取(人),从教师中抽取(人),从后勤人员中抽取(人);
第三步,采用简单随机抽样的方法,抽取行政人员2人,教师人员14人,后勤人员4人;
第四步,把抽取的个体组合在一起构成所需样本.
学以致用
学以致用
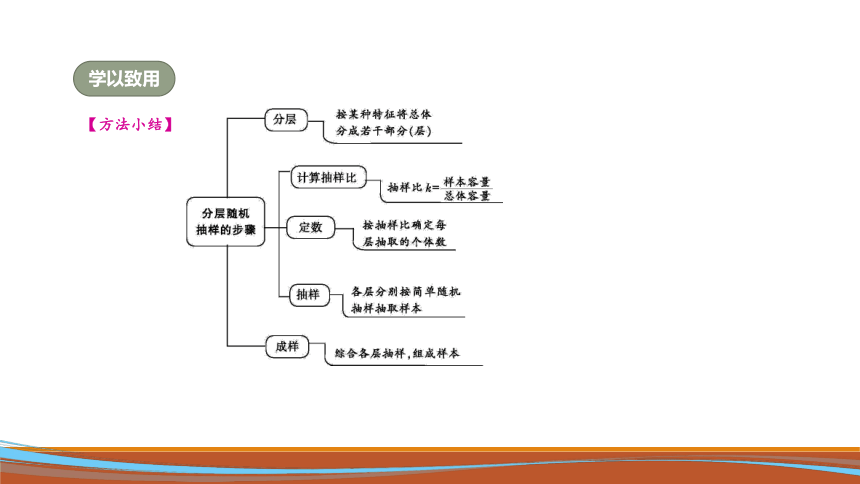
【方法小结】
【针对训练】某网站针对“2021年法定节假日调休安排”提出的,,三种放假方案进行了问卷调查,调查结果如下:
支持方案 支持方案 支持方案
35岁以下的人数 210 400 800
35岁以上(含35岁)的人数 100 100 400
(1)从所有参与调查的人中,用分层随机抽样的方法抽取人,已知从支持方案的人中抽取了6人,求的值;
(2)从支持方案的人中,用分层随机抽样的方法抽取5人,这5人中在35岁以上(含35岁)的人数是多少 35岁以下的人数是多少
【解析】(1)先确定抽样比,然后建立等式求解;(2)直接用抽样比乘支持方案年龄段的人数即可.
【针对训练】某网站针对“2021年法定节假日调休安排”提出的A,B,C三种放假方案进行了问卷调查,调查结果如下:
支持方案 支持方案 支持方案
35岁以下的人数 210 400 800
35岁以上(含35岁)的人数 100 100 400
(1)从所有参与调查的人中,用分层随机抽样的方法抽取人,已知从支持方案的人中抽取了6人,求的值;
【答案】(1)由题意得
,
解得,所以.
【针对训练】某网站针对“2021年法定节假日调休安排”提出的A,B,C三种放假方案进行了问卷调查,调查结果如下:
支持方案 支持方案 支持方案
35岁以下的人数 210 400 800
35岁以上(含35岁)的人数 100 100 400
(2)从支持方案的人中,用分层随机抽样的方法抽取5人,这5人中在35岁以上(含35岁)的人数是多少 35岁以下的人数是多少
【答案】(2)35岁以下的人数为,35岁以上(含35岁)的人数为.
2.抽样方法的选取
【问题情境】为了能让玉树地震灾区人民早日重建家园,学校团委号召全校1200名学生开展“情系玉树,大爱无疆”抗震救灾捐款活动.为了能及时了解学生的捐款情况,校团委准备从全校学生中选取60名学生进行调查,但在对待样本的抽取方法上团委会有三种意见.
宣传委员说:“因为我在七(3)班,我对七年级学生比较熟悉,就从我们七年级学生中用简单随机抽样抽取60名学生进行调查吧.”
组织委员说:“我是女生,我对女生比较了解,就从女生中用简单随机抽样抽取60名学生进行调查吧.”
团委副书记说:“我觉得应该是从全校学生中用简单随机抽样抽取60名学生进行调查比较合理.”
2.抽样方法的选取
【问题1】宣传委员的抽取方法合理吗
【答案】宣传委员的抽取方法不合理,由于只在七年级学生中抽取,没有反映其他年级学生的捐款情况,所以不符合抽样的要求.
【问题2】组织委员说的合理吗
【答案】组织委员说的不合理,男、女学生有差异,不能用女学生的捐款情况代表全校学生的捐款情况..
【问题3】团委副书记说的合理吗
【答案】与方案一、方案二相比,方案三可以更好地反映全校学生的捐款情况
抽样方法的选择
在解决实际问题时,大部分情况不止采用一种抽样方法,而会采用多种方法进行抽样调查.在统计的全过程中,对数据来源的科学认识是至关重要的.选取与实际问题相适宜的抽样方法,直接关系到数据的可靠性.
抽象概括
【例2】选择合适的抽样方法抽样,并写出抽样过程.
(1)有甲厂生产的30个篮球,其中一箱21个,另一箱9个,抽取3个;
(2)有30个篮球,其中甲厂生产的有21个,乙厂生产的有9个,抽取10个;
(3)有甲厂生产的300个篮球,抽取10个.
学以致用
学以致用
【解析】(1)总体容量较小,用抽签法.
①将30个篮球进行编号,编号为00,01,…,29;
②将以上30个编号分别写在完全一样的一张小纸条上,揉成小球,制成号签;
③把号签放入一个不透明的袋子中,充分搅拌;
④从袋子中逐个抽取3个号签,并记录上面的号码;
⑤找出和所得号码对应的篮球即可得到样本.
(2)总体由差异明显的两个层次组成,需选用分层随机抽样法.
①确定抽取个数.抽样比为,所以甲厂生产的篮球应抽取(个),乙厂生产的篮球应抽取(个);
②用抽签法分别抽取甲厂生产的篮球7个,乙厂生产的篮球3个,这些篮球便组成了我们要抽取的样本.
【方法指导】由题目可获取以下主要信息:①本题是要求选择适当的抽样方法.②要写出抽样过程.解答本题应综合三种抽样方法的适用范围和实际情况,灵活选取适当的方法进行抽取.
学以致用
【解析】 (3)总体容量较大,样本容量较小,宜用随机数法.
①将300个篮球用随机方式编号,编号为001,002,…,300;
②在随机数表(见课本)中随机的确定一个数作为开始,如第8行第29列的数“1”开始,任选一个方向作为读数方向,比如向右读;
③从数“1”开始向右读,每次读三位,凡不在001~300中的数跳过去不读,遇到已经读过的数也跳过去不读,便可依次得到10个号码,这就是所要抽取的10个样本个体的号码.
【方法指导】由题目可获取以下主要信息:①本题是要求选择适当的抽样方法.②要写出抽样过程.解答本题应综合三种抽样方法的适用范围和实际情况,灵活选取适当的方法进行抽取.
【方法小结】分层随机抽样是当总体由差异明显的几部分组成时采用的抽样方法:
(1)分层抽样中分多少层、如何分层要视具体情况而定,总的原则是:层内样本的差异要小,各层之间的样本差异要大,且互不重叠.
(2)为了保证每个个体等可能入样,所有层应采用同一抽样比,等可能抽样.
(3)在每层抽样时,应采用简单随机抽样的方法进行抽样
【针对训练】一个单位有职工160人,其中业务人员96人,管理人员40人,后勤服务人员24人.为了了解职工的某种情况,要从中抽取一个容量为20的样本,按下述两种方法抽样:
方法1:将160人从1至160编上号,然后将160个编号分别写在完全一样的小纸条上,揉成小球放入箱内拌匀,然后从中抽20个号签,与所得号码对应的20个人被选出.
方法2:按20∶160=1∶8的比例,从业务人员中抽取12人,从管理人员中抽取5人,从后勤服务人员中抽取3人,都用随机数法从各类人员中抽取所需的人数,他们合在一起恰好抽到20人.
则方案1是____________,方案2是_______________.(填简单随机抽样、分层随机抽样)
【解析】方法1是简单随机抽样;方法2是分层随机抽样.
简单随机抽样
分层随机抽样
【例3】为了对某课题进行研究,分别从,,三所高校中用分层随机抽样法抽取若干名教授组成研究小组,其中高校有名教授,高校有72名教授,高校有名教授(其中).
(1)若,两所高校中共抽取3名教授,,两所高校中共抽取5名教授,求,;
(2)若高校中抽取的教授数是高校和中抽取的教授总数的,求三所高校的教授的总人数.
探究:方程思想在分层随机抽样中的应用
【方法指导】(1)由题意得高校中抽取2名教授,高校中抽取1名教授,高校中抽取3名教授,再利用分层随机抽样的特征建立方程求解;(2)由题意,结合分层随机抽样的特征建立方程求即可得解.
【例3】为了对某课题进行研究,分别从,,三所高校中用分层随机抽样法抽取若干名教授组成研究小组,其中高校有名教授,高校有72名教授,高校有名教授(其中).
(1)若,两所高校中共抽取3名教授,,两所高校中共抽取5名教授,求,;
(2)若高校中抽取的教授数是高校和中抽取的教授总数的,求三所高校的教授的总人数.
探究:方程思想在分层随机抽样中的应用
【解析】(1)∵,,两所高校中共抽取3名教授,,两所高校中共抽取5名教授,∴高校中抽取2名教授,高校中抽取1名教授,高校中抽取3名教授,
∴,解得,.
(2)∵高校中抽取的教授数是高校和中抽取的教授总数的,∴,解得,∴三所高校的教授的总人数为.
探究:方程思想在分层随机抽样中的应用
【探究小结】进行分层随机抽样的相关计算时,常利用以下关系式,转化为按比例列方程或算式求解:(1);
(2)总体中某两层的个体数之比等于样本中这两层抽取的个体数之比.
【针对训练】为了了解某社区居民有无收看“奥运会开幕式”的情况,某记者分别从该社区60~70岁,40~50岁,20~30岁的三个年龄段中的160人,240人,人中,采用分层随机抽样的方法共抽取了30人进行调查,若在60~70岁这个年龄段中抽查了8人,则为( ).
A.90 B.120 C.180 D.200
【解析】从60~70岁,40~50岁,20~30岁的三个年龄段中的160人,240人,人中抽取30人,每个个体被抽到的概率为,
∵在60~70岁这个年龄段中抽查了8人,∴,解得.
D
1. ①某班元旦聚会,要产生两名“幸运者”.②某班期中考试有15人在85分以上,40人在60~84分,1人不及格.现欲从中抽出8人研讨进一步改进教和学,合适的抽样方法分别为( ).
A.分层随机抽样,简单随机抽样
B.分层随机抽样,分层随机抽样
C.简单随机抽样,简单随机抽样
D.简单随机抽样,分层随机抽样
2.甲校有3600名学生,乙校有5400名学生,丙校有1800名学生,为统计三校学生某方面的情况,计划采用分层随机抽样法抽取一个样本量为90的样本,应在甲、乙、丙三校分别抽取学生( ).
A.30人,30人,30人 B.30人,45人,15人
C.20人,30人,40人 D.30人,50人,10人
3.某校500名学生中,型血有200人,型血有125人,型血有125人,型血有50人,为了研究血型与色弱的关系,需从中抽取一个样本量为20的样本.按照比例分配的分层随机抽样方法抽取样本,各种血型的人分别抽多少
【解析】①某班元旦聚会,要产生两名“幸运者”,总体和样本容量都不大,所以采用简单随机抽样.
②某班期中考试有15人在85分以上,40人在60~84分,1人不及格.现欲从中抽出8人研讨进一步改进教和学,总体由具有明显差异的几个部分组成,所以采用分层随机抽样.
1. ①某班元旦聚会,要产生两名“幸运者”.②某班期中考试有15人在85分以上,40人在60~84分,1人不及格.现欲从中抽出8人研讨进一步改进教和学,合适的抽样方法分别为( ).
A.分层随机抽样,简单随机抽样
B.分层随机抽样,分层随机抽样
C.简单随机抽样,简单随机抽样
D.简单随机抽样,分层随机抽样
D
【解析】先求抽样比,各层再按抽样比分别抽取,甲校抽取(人);乙校抽取(人);丙校抽取(人).故选B.
B
2.甲校有3600名学生,乙校有5400名学生,丙校有1800名学生,为统计三校学生某方面的情况,计划采用分层随机抽样法抽取一个样本量为90的样本,应在甲、乙、丙三校分别抽取学生( ).
A.30人,30人,30人 B.30人,45人,15人
C.20人,30人,40人 D.30人,50人,10人
【解析】∵,∴,,.
故型血抽8人,型血抽5人,型血抽5人,型血抽2人.
3.某校500名学生中,型血有200人,型血有125人,型血有125人,型血有50人,为了研究血型与色弱的关系,需从中抽取一个样本量为20的样本.按照比例分配的分层随机抽样方法抽取样本,各种血型的人分别抽多少
6.2.2 分层随机抽样
某电视台在互联网上就观众对某一节目的喜爱程度进行调查,参加调查的总人数为12 000人,其中持各种态度的人数分别为:很喜欢4 800人,喜欢3 600人,一般1 800人,不喜欢1 800人.电视台为进一步了解观众的具体想法和意见,打算从这12 000人中抽取60人进行更为详细的调查,应采取什么样的抽样方法呢
1.分层随机抽样的相关概念
【答案】小学生、初中生、高中生三个群体在年龄、体质等方面存在着明显的差异.
【问题情境】某市为调查中小学生的近视情况,在全市范围内分别对小学生、初中生、高中生三个群体抽样,进而了解中小学生的总体情况和三个群体近视情况的差异大小
【问题1】上述问题中总体有什么特征
【答案】抽取的样本可能集中于某一个群体,不具有代表性.
【问题2】若采用抽签法或随机数法抽样会出现什么结果
【问题3】为使抽取的样本更合理,更具有代表性,有更好的抽样方法解决该问题吗
【答案】有,可分不同群体抽取.
【问题4】层随机抽样的总体具有什么特性
【答案】分层随机抽样的总体按一个或多个变量划分成若干个子总体,并且每一个个体属于且仅属于一个子总体.
分层随机抽样的概念
将总体按其属性特征分成互不交叉的若干类型(有时称作层),然后在每个类型中按照所占比例随机抽取一定的个体,这种抽样方法通常叫作分层随机抽样.
特别提醒:分层随机抽样的特点
由于层与层之间有明显的区别,而层内个体间的差异不明显,所以在抽取样本时,一般在每层进行简单随机抽样,以保证公平、公正,在实际操作时,应先计算抽样比,然后计算每层需要抽取的个数:抽样比×该层个体数目=.
抽象概括
【例1】某学校有在职人员160人,其中行政人员有16人,教师有112人,后勤人员有32人.教育部门为了了解在职人员对学校机构改革的意见,要从中抽取一个容量为20的样本,请利用分层随机抽样的方法抽取,并写出抽样过程.
【解析】抽样过程如下:
第一步,确定抽样比,样本容量与总体容量的比为;
第二步,确定分别从三类人员中抽取的人数,从行政人员中抽取(人),从教师中抽取(人),从后勤人员中抽取(人);
第三步,采用简单随机抽样的方法,抽取行政人员2人,教师人员14人,后勤人员4人;
第四步,把抽取的个体组合在一起构成所需样本.
学以致用
学以致用
【方法小结】
【针对训练】某网站针对“2021年法定节假日调休安排”提出的,,三种放假方案进行了问卷调查,调查结果如下:
支持方案 支持方案 支持方案
35岁以下的人数 210 400 800
35岁以上(含35岁)的人数 100 100 400
(1)从所有参与调查的人中,用分层随机抽样的方法抽取人,已知从支持方案的人中抽取了6人,求的值;
(2)从支持方案的人中,用分层随机抽样的方法抽取5人,这5人中在35岁以上(含35岁)的人数是多少 35岁以下的人数是多少
【解析】(1)先确定抽样比,然后建立等式求解;(2)直接用抽样比乘支持方案年龄段的人数即可.
【针对训练】某网站针对“2021年法定节假日调休安排”提出的A,B,C三种放假方案进行了问卷调查,调查结果如下:
支持方案 支持方案 支持方案
35岁以下的人数 210 400 800
35岁以上(含35岁)的人数 100 100 400
(1)从所有参与调查的人中,用分层随机抽样的方法抽取人,已知从支持方案的人中抽取了6人,求的值;
【答案】(1)由题意得
,
解得,所以.
【针对训练】某网站针对“2021年法定节假日调休安排”提出的A,B,C三种放假方案进行了问卷调查,调查结果如下:
支持方案 支持方案 支持方案
35岁以下的人数 210 400 800
35岁以上(含35岁)的人数 100 100 400
(2)从支持方案的人中,用分层随机抽样的方法抽取5人,这5人中在35岁以上(含35岁)的人数是多少 35岁以下的人数是多少
【答案】(2)35岁以下的人数为,35岁以上(含35岁)的人数为.
2.抽样方法的选取
【问题情境】为了能让玉树地震灾区人民早日重建家园,学校团委号召全校1200名学生开展“情系玉树,大爱无疆”抗震救灾捐款活动.为了能及时了解学生的捐款情况,校团委准备从全校学生中选取60名学生进行调查,但在对待样本的抽取方法上团委会有三种意见.
宣传委员说:“因为我在七(3)班,我对七年级学生比较熟悉,就从我们七年级学生中用简单随机抽样抽取60名学生进行调查吧.”
组织委员说:“我是女生,我对女生比较了解,就从女生中用简单随机抽样抽取60名学生进行调查吧.”
团委副书记说:“我觉得应该是从全校学生中用简单随机抽样抽取60名学生进行调查比较合理.”
2.抽样方法的选取
【问题1】宣传委员的抽取方法合理吗
【答案】宣传委员的抽取方法不合理,由于只在七年级学生中抽取,没有反映其他年级学生的捐款情况,所以不符合抽样的要求.
【问题2】组织委员说的合理吗
【答案】组织委员说的不合理,男、女学生有差异,不能用女学生的捐款情况代表全校学生的捐款情况..
【问题3】团委副书记说的合理吗
【答案】与方案一、方案二相比,方案三可以更好地反映全校学生的捐款情况
抽样方法的选择
在解决实际问题时,大部分情况不止采用一种抽样方法,而会采用多种方法进行抽样调查.在统计的全过程中,对数据来源的科学认识是至关重要的.选取与实际问题相适宜的抽样方法,直接关系到数据的可靠性.
抽象概括
【例2】选择合适的抽样方法抽样,并写出抽样过程.
(1)有甲厂生产的30个篮球,其中一箱21个,另一箱9个,抽取3个;
(2)有30个篮球,其中甲厂生产的有21个,乙厂生产的有9个,抽取10个;
(3)有甲厂生产的300个篮球,抽取10个.
学以致用
学以致用
【解析】(1)总体容量较小,用抽签法.
①将30个篮球进行编号,编号为00,01,…,29;
②将以上30个编号分别写在完全一样的一张小纸条上,揉成小球,制成号签;
③把号签放入一个不透明的袋子中,充分搅拌;
④从袋子中逐个抽取3个号签,并记录上面的号码;
⑤找出和所得号码对应的篮球即可得到样本.
(2)总体由差异明显的两个层次组成,需选用分层随机抽样法.
①确定抽取个数.抽样比为,所以甲厂生产的篮球应抽取(个),乙厂生产的篮球应抽取(个);
②用抽签法分别抽取甲厂生产的篮球7个,乙厂生产的篮球3个,这些篮球便组成了我们要抽取的样本.
【方法指导】由题目可获取以下主要信息:①本题是要求选择适当的抽样方法.②要写出抽样过程.解答本题应综合三种抽样方法的适用范围和实际情况,灵活选取适当的方法进行抽取.
学以致用
【解析】 (3)总体容量较大,样本容量较小,宜用随机数法.
①将300个篮球用随机方式编号,编号为001,002,…,300;
②在随机数表(见课本)中随机的确定一个数作为开始,如第8行第29列的数“1”开始,任选一个方向作为读数方向,比如向右读;
③从数“1”开始向右读,每次读三位,凡不在001~300中的数跳过去不读,遇到已经读过的数也跳过去不读,便可依次得到10个号码,这就是所要抽取的10个样本个体的号码.
【方法指导】由题目可获取以下主要信息:①本题是要求选择适当的抽样方法.②要写出抽样过程.解答本题应综合三种抽样方法的适用范围和实际情况,灵活选取适当的方法进行抽取.
【方法小结】分层随机抽样是当总体由差异明显的几部分组成时采用的抽样方法:
(1)分层抽样中分多少层、如何分层要视具体情况而定,总的原则是:层内样本的差异要小,各层之间的样本差异要大,且互不重叠.
(2)为了保证每个个体等可能入样,所有层应采用同一抽样比,等可能抽样.
(3)在每层抽样时,应采用简单随机抽样的方法进行抽样
【针对训练】一个单位有职工160人,其中业务人员96人,管理人员40人,后勤服务人员24人.为了了解职工的某种情况,要从中抽取一个容量为20的样本,按下述两种方法抽样:
方法1:将160人从1至160编上号,然后将160个编号分别写在完全一样的小纸条上,揉成小球放入箱内拌匀,然后从中抽20个号签,与所得号码对应的20个人被选出.
方法2:按20∶160=1∶8的比例,从业务人员中抽取12人,从管理人员中抽取5人,从后勤服务人员中抽取3人,都用随机数法从各类人员中抽取所需的人数,他们合在一起恰好抽到20人.
则方案1是____________,方案2是_______________.(填简单随机抽样、分层随机抽样)
【解析】方法1是简单随机抽样;方法2是分层随机抽样.
简单随机抽样
分层随机抽样
【例3】为了对某课题进行研究,分别从,,三所高校中用分层随机抽样法抽取若干名教授组成研究小组,其中高校有名教授,高校有72名教授,高校有名教授(其中).
(1)若,两所高校中共抽取3名教授,,两所高校中共抽取5名教授,求,;
(2)若高校中抽取的教授数是高校和中抽取的教授总数的,求三所高校的教授的总人数.
探究:方程思想在分层随机抽样中的应用
【方法指导】(1)由题意得高校中抽取2名教授,高校中抽取1名教授,高校中抽取3名教授,再利用分层随机抽样的特征建立方程求解;(2)由题意,结合分层随机抽样的特征建立方程求即可得解.
【例3】为了对某课题进行研究,分别从,,三所高校中用分层随机抽样法抽取若干名教授组成研究小组,其中高校有名教授,高校有72名教授,高校有名教授(其中).
(1)若,两所高校中共抽取3名教授,,两所高校中共抽取5名教授,求,;
(2)若高校中抽取的教授数是高校和中抽取的教授总数的,求三所高校的教授的总人数.
探究:方程思想在分层随机抽样中的应用
【解析】(1)∵,,两所高校中共抽取3名教授,,两所高校中共抽取5名教授,∴高校中抽取2名教授,高校中抽取1名教授,高校中抽取3名教授,
∴,解得,.
(2)∵高校中抽取的教授数是高校和中抽取的教授总数的,∴,解得,∴三所高校的教授的总人数为.
探究:方程思想在分层随机抽样中的应用
【探究小结】进行分层随机抽样的相关计算时,常利用以下关系式,转化为按比例列方程或算式求解:(1);
(2)总体中某两层的个体数之比等于样本中这两层抽取的个体数之比.
【针对训练】为了了解某社区居民有无收看“奥运会开幕式”的情况,某记者分别从该社区60~70岁,40~50岁,20~30岁的三个年龄段中的160人,240人,人中,采用分层随机抽样的方法共抽取了30人进行调查,若在60~70岁这个年龄段中抽查了8人,则为( ).
A.90 B.120 C.180 D.200
【解析】从60~70岁,40~50岁,20~30岁的三个年龄段中的160人,240人,人中抽取30人,每个个体被抽到的概率为,
∵在60~70岁这个年龄段中抽查了8人,∴,解得.
D
1. ①某班元旦聚会,要产生两名“幸运者”.②某班期中考试有15人在85分以上,40人在60~84分,1人不及格.现欲从中抽出8人研讨进一步改进教和学,合适的抽样方法分别为( ).
A.分层随机抽样,简单随机抽样
B.分层随机抽样,分层随机抽样
C.简单随机抽样,简单随机抽样
D.简单随机抽样,分层随机抽样
2.甲校有3600名学生,乙校有5400名学生,丙校有1800名学生,为统计三校学生某方面的情况,计划采用分层随机抽样法抽取一个样本量为90的样本,应在甲、乙、丙三校分别抽取学生( ).
A.30人,30人,30人 B.30人,45人,15人
C.20人,30人,40人 D.30人,50人,10人
3.某校500名学生中,型血有200人,型血有125人,型血有125人,型血有50人,为了研究血型与色弱的关系,需从中抽取一个样本量为20的样本.按照比例分配的分层随机抽样方法抽取样本,各种血型的人分别抽多少
【解析】①某班元旦聚会,要产生两名“幸运者”,总体和样本容量都不大,所以采用简单随机抽样.
②某班期中考试有15人在85分以上,40人在60~84分,1人不及格.现欲从中抽出8人研讨进一步改进教和学,总体由具有明显差异的几个部分组成,所以采用分层随机抽样.
1. ①某班元旦聚会,要产生两名“幸运者”.②某班期中考试有15人在85分以上,40人在60~84分,1人不及格.现欲从中抽出8人研讨进一步改进教和学,合适的抽样方法分别为( ).
A.分层随机抽样,简单随机抽样
B.分层随机抽样,分层随机抽样
C.简单随机抽样,简单随机抽样
D.简单随机抽样,分层随机抽样
D
【解析】先求抽样比,各层再按抽样比分别抽取,甲校抽取(人);乙校抽取(人);丙校抽取(人).故选B.
B
2.甲校有3600名学生,乙校有5400名学生,丙校有1800名学生,为统计三校学生某方面的情况,计划采用分层随机抽样法抽取一个样本量为90的样本,应在甲、乙、丙三校分别抽取学生( ).
A.30人,30人,30人 B.30人,45人,15人
C.20人,30人,40人 D.30人,50人,10人
【解析】∵,∴,,.
故型血抽8人,型血抽5人,型血抽5人,型血抽2人.
3.某校500名学生中,型血有200人,型血有125人,型血有125人,型血有50人,为了研究血型与色弱的关系,需从中抽取一个样本量为20的样本.按照比例分配的分层随机抽样方法抽取样本,各种血型的人分别抽多少
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
