2013-2014学年九年级数学(湘教版)上册第4章 锐角三角函数 检测题(含答案详解)
文档属性
| 名称 | 2013-2014学年九年级数学(湘教版)上册第4章 锐角三角函数 检测题(含答案详解) |

|
|
| 格式 | zip | ||
| 文件大小 | 401.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-10 00:00:00 | ||
图片预览



文档简介
第4章 锐角三角函数检测题
(本检测题满分:120分,时间:120分钟)
一、选择题(每小题3分,共30分)
1.(2013·天津中考)的值等于( )
A.1 B. C. D.2
2.(2013·重庆中考)计算的结果是( )
A. B. C. D.
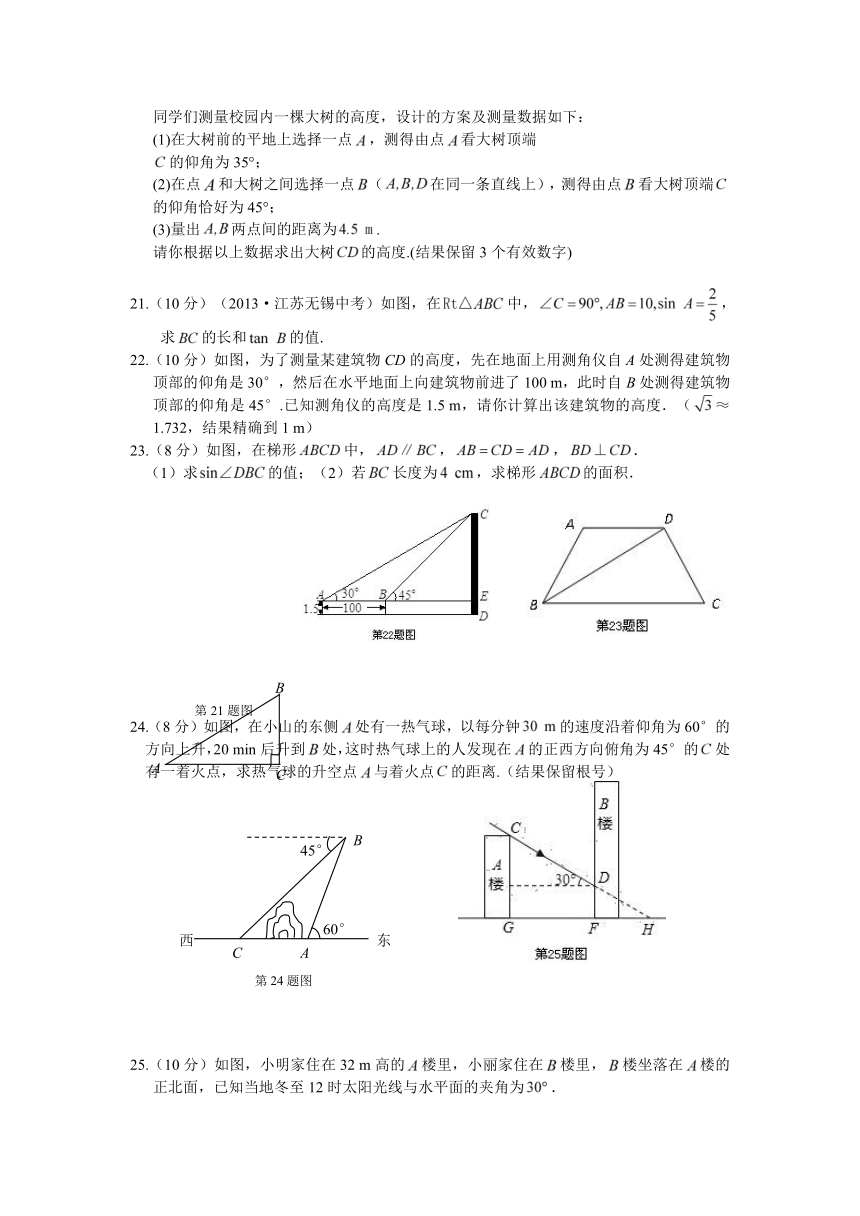
3.(2013·浙江温州中考)如图,在中,
则的值是( )
A. B.
C. D.
4.下列说法中,正确的是( )
A.
B.若为锐角,则
C.对于锐角 QUOTE ,必有
D.
5.在中,,,则的值是( )
A. B. C. 1 D.
6.已知在中,,则的值为( )
A. B. C. D.
7.如图,一个小球由地面沿着坡度的坡面向上前进了10 m,此时小球距离地面的高度为( )
A.5 m B.2 m
C.4 m D.m
8.如图,在菱形中,,,,则的值是( )
A. B.2 C. D.
9.在△中,,,则等于( )
A. B.1 C.2 D.3
10.如图,已知:45°<∠A<90°,则下列各式成立的是( )
A. B. C. D.
二、填空题(每小题3分,共24分)
11.(2013·广东中考)在中,,则______.
12.(2013·陕西中考)比较大小: .(填“>”“=”或“<”)
13.如图,小兰想测量南塔的高度,她在处仰望塔顶,测得仰角为30°,再往塔的方向前进50 m至处,测得仰角为60°,那么塔高约为 _________ m.(小兰身高忽略不计,)
14.已知等腰三角形的腰长为2,腰上的高为1,则它的底角等于________.
15.大坝的横断面是梯形,坝内斜坡的坡度,坝外斜坡的坡度,则两个
坡角的和为 .
16.如图,△ABC的顶点都在方格纸的格点上,则_ .
17.如图,在四边形中,,则__________.
18.如图,在△ QUOTE 中,已知,则________.
三、解答题(共66分)
19.(8分)计算下列各题:
(1);(2).
20.(12分)在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树的高度,设计的方案及测量数据如下:
(1)在大树前的平地上选择一点,测得由点看大树顶端
的仰角为35°;
(2)在点和大树之间选择一点(在同一条直线上),测得由点看大树顶端的仰角恰好为45°;
(3)量出两点间的距离为.
请你根据以上数据求出大树的高度.(结果保留3个有效数字)
21.(10分)(2013·江苏无锡中考)如图,在中,,求的长和的值.
22.(10分)如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100 m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5 m,请你计算出该建筑物的高度.(≈1.732,结果精确到1 m)
23.(8分)如图,在梯形中,,,.
(1)求的值;(2)若长度为,求梯形的面积.
24.(8分)如图,在小山的东侧处有一热气球,以每分钟的速度沿着仰角为60°的方向上升,20 min后升到处,这时热气球上的人发现在的正西方向俯角为45°的处有一着火点,求热气球的升空点与着火点的距离.(结果保留根号)
25.(10分)如图,小明家住在32 m高的楼里,小丽家住在 QUOTE 楼里,楼坐落在楼的正北面,已知当地冬至12时太阳光线与水平面的夹角为.
(1)如果 QUOTE 两楼相距 m,那么楼落在楼上的影子有多长?
(2)如果 QUOTE 楼的影子刚好不落在 QUOTE 楼上,那么两楼的距离应是多少?(结果保留根号)
第4章 锐角三角函数检测题参考答案
1.C
2.D 解析:.
3.C 解析:.
4.B 解析:因为,
所以,故错;
因为,所以,故B正确;
当时,,所以,故C错;
因为,所以,故D错.
5.B 解析:因为∠=90°,,
所以.
6.A 解析:如图,设则由勾股定理知,所以
7.B 解析:设小球距离地面的高度为则小球水平移动的距离为
所以解得
8.B 解析:设又因为在菱形中,
所以所以
所以
由勾股定理知所以2
9.B 解析:∵ 在△中,,,,
∴ ,∴ .故选B.
10.B 解析:在锐角三角函数中仅当45°时,,所以选项错误;
因为45°<∠A<90°,所以∠B<45°,即∠A>∠B,所以BC>AC,所以,即 QUOTE ,所以选项正确,选项错误 >1,<1,所以选项错误.
11. 解析:在中,,由勾股定理,得,
所以,所以.
12.> 解析:因为,所以∠.
13.43.3 解析:因为,所以
所以所以.
14.15°或75° 解析:如图,.在图①中,,
所以∠∠;在图②中,,所以∠∠.
15. 解析:设两个坡角分别为,,则tan,tan,所以,所以两个坡角的和为.
16. 解析:利用网格,过点向所在直线作垂线,设网格中小正方形的边长为1,则利用勾股定理得,所以.
17. 解析:如图,延长,交于点.
∵ ∠,∴ .
∵ ,∴ ,则.
∵ ,∴ .
18.6 解析:如图,过点作于点.
∵ ,∠,∴ .
∴ .
19.解:(1)
(2).
20.解:∵ ∠90°, ∠45°,∴
∵ ,∴
设高为,则 m,.
∵ ∠35°,∴ tan∠tan 35°.
整理,得≈10.5.
故大树的高度约为10.5
21.解:∵ ∴ .
又∵ ∴ .
22.解:设,则由题意可知,m.
在Rt△AEC中,tan∠CAE=,即tan 30°=.
∴ ,即3x(x+100),解得x50+50.
经检验50+50是原方程的解.
∴ CDCEED≈136.61.5138.1≈.
故该建筑物的高度约为.
23.解:(1)∵ ,∴ ∠∠.
∵ ∥,∴ ∠∠∠.
在梯形中,∵ ,
∴ ∠∠∠∠
∵ ,∴ 3∠,
∴ ∠30°,∴
(2)如图,过点作于点.
在Rt△中, ∠,
∠,∴
在Rt△中,,
∴ 梯形的面积为
24.解:过点作于点..
因为∠,300 m,
所以300(-1)即热气球的升空点与着火点的距离为300(-1)
25.解:(1)如图,过点作于点,
∵ ,,
∴ .
故.
∴ 楼落在楼上的影子有12 m长.
(2)若楼的影子刚好不落在楼上,
,
∴ 两楼的距离应是m.
A
C
B
第3题图
第7题图
A
B
C
第10题图
A
C
B
第18题图
C
A
B
第21题图
B
C
A
东
西
45°
60°
第24题图
A
C
B
第6题答图
第14题答图
(本检测题满分:120分,时间:120分钟)
一、选择题(每小题3分,共30分)
1.(2013·天津中考)的值等于( )
A.1 B. C. D.2
2.(2013·重庆中考)计算的结果是( )
A. B. C. D.
3.(2013·浙江温州中考)如图,在中,
则的值是( )
A. B.
C. D.
4.下列说法中,正确的是( )
A.
B.若为锐角,则
C.对于锐角 QUOTE ,必有
D.
5.在中,,,则的值是( )
A. B. C. 1 D.
6.已知在中,,则的值为( )
A. B. C. D.
7.如图,一个小球由地面沿着坡度的坡面向上前进了10 m,此时小球距离地面的高度为( )
A.5 m B.2 m
C.4 m D.m
8.如图,在菱形中,,,,则的值是( )
A. B.2 C. D.
9.在△中,,,则等于( )
A. B.1 C.2 D.3
10.如图,已知:45°<∠A<90°,则下列各式成立的是( )
A. B. C. D.
二、填空题(每小题3分,共24分)
11.(2013·广东中考)在中,,则______.
12.(2013·陕西中考)比较大小: .(填“>”“=”或“<”)
13.如图,小兰想测量南塔的高度,她在处仰望塔顶,测得仰角为30°,再往塔的方向前进50 m至处,测得仰角为60°,那么塔高约为 _________ m.(小兰身高忽略不计,)
14.已知等腰三角形的腰长为2,腰上的高为1,则它的底角等于________.
15.大坝的横断面是梯形,坝内斜坡的坡度,坝外斜坡的坡度,则两个
坡角的和为 .
16.如图,△ABC的顶点都在方格纸的格点上,则_ .
17.如图,在四边形中,,则__________.
18.如图,在△ QUOTE 中,已知,则________.
三、解答题(共66分)
19.(8分)计算下列各题:
(1);(2).
20.(12分)在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树的高度,设计的方案及测量数据如下:
(1)在大树前的平地上选择一点,测得由点看大树顶端
的仰角为35°;
(2)在点和大树之间选择一点(在同一条直线上),测得由点看大树顶端的仰角恰好为45°;
(3)量出两点间的距离为.
请你根据以上数据求出大树的高度.(结果保留3个有效数字)
21.(10分)(2013·江苏无锡中考)如图,在中,,求的长和的值.
22.(10分)如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100 m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5 m,请你计算出该建筑物的高度.(≈1.732,结果精确到1 m)
23.(8分)如图,在梯形中,,,.
(1)求的值;(2)若长度为,求梯形的面积.
24.(8分)如图,在小山的东侧处有一热气球,以每分钟的速度沿着仰角为60°的方向上升,20 min后升到处,这时热气球上的人发现在的正西方向俯角为45°的处有一着火点,求热气球的升空点与着火点的距离.(结果保留根号)
25.(10分)如图,小明家住在32 m高的楼里,小丽家住在 QUOTE 楼里,楼坐落在楼的正北面,已知当地冬至12时太阳光线与水平面的夹角为.
(1)如果 QUOTE 两楼相距 m,那么楼落在楼上的影子有多长?
(2)如果 QUOTE 楼的影子刚好不落在 QUOTE 楼上,那么两楼的距离应是多少?(结果保留根号)
第4章 锐角三角函数检测题参考答案
1.C
2.D 解析:.
3.C 解析:.
4.B 解析:因为,
所以,故错;
因为,所以,故B正确;
当时,,所以,故C错;
因为,所以,故D错.
5.B 解析:因为∠=90°,,
所以.
6.A 解析:如图,设则由勾股定理知,所以
7.B 解析:设小球距离地面的高度为则小球水平移动的距离为
所以解得
8.B 解析:设又因为在菱形中,
所以所以
所以
由勾股定理知所以2
9.B 解析:∵ 在△中,,,,
∴ ,∴ .故选B.
10.B 解析:在锐角三角函数中仅当45°时,,所以选项错误;
因为45°<∠A<90°,所以∠B<45°,即∠A>∠B,所以BC>AC,所以,即 QUOTE ,所以选项正确,选项错误 >1,<1,所以选项错误.
11. 解析:在中,,由勾股定理,得,
所以,所以.
12.> 解析:因为,所以∠.
13.43.3 解析:因为,所以
所以所以.
14.15°或75° 解析:如图,.在图①中,,
所以∠∠;在图②中,,所以∠∠.
15. 解析:设两个坡角分别为,,则tan,tan,所以,所以两个坡角的和为.
16. 解析:利用网格,过点向所在直线作垂线,设网格中小正方形的边长为1,则利用勾股定理得,所以.
17. 解析:如图,延长,交于点.
∵ ∠,∴ .
∵ ,∴ ,则.
∵ ,∴ .
18.6 解析:如图,过点作于点.
∵ ,∠,∴ .
∴ .
19.解:(1)
(2).
20.解:∵ ∠90°, ∠45°,∴
∵ ,∴
设高为,则 m,.
∵ ∠35°,∴ tan∠tan 35°.
整理,得≈10.5.
故大树的高度约为10.5
21.解:∵ ∴ .
又∵ ∴ .
22.解:设,则由题意可知,m.
在Rt△AEC中,tan∠CAE=,即tan 30°=.
∴ ,即3x(x+100),解得x50+50.
经检验50+50是原方程的解.
∴ CDCEED≈136.61.5138.1≈.
故该建筑物的高度约为.
23.解:(1)∵ ,∴ ∠∠.
∵ ∥,∴ ∠∠∠.
在梯形中,∵ ,
∴ ∠∠∠∠
∵ ,∴ 3∠,
∴ ∠30°,∴
(2)如图,过点作于点.
在Rt△中, ∠,
∠,∴
在Rt△中,,
∴ 梯形的面积为
24.解:过点作于点..
因为∠,300 m,
所以300(-1)即热气球的升空点与着火点的距离为300(-1)
25.解:(1)如图,过点作于点,
∵ ,,
∴ .
故.
∴ 楼落在楼上的影子有12 m长.
(2)若楼的影子刚好不落在楼上,
,
∴ 两楼的距离应是m.
A
C
B
第3题图
第7题图
A
B
C
第10题图
A
C
B
第18题图
C
A
B
第21题图
B
C
A
东
西
45°
60°
第24题图
A
C
B
第6题答图
第14题答图
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
