有理数的乘方(1)[上学期]
文档属性
| 名称 | 有理数的乘方(1)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 119.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-05-25 00:00:00 | ||
图片预览










文档简介
课件31张PPT。你信吗? 一张厚为0.1毫米的纸折叠27次后,它的厚度相当于1.5个珠穆朗玛峰有理数的乘方大溪四中 项连玺 练习一(课前测评)
1、边长为 的正方形的面积为 ;
2、棱长为 的正方体的体积为 ;
3、(-2)×(-2)×(-2)= ;
4、(-1)×(-2)×(-3)×(-4)×5= ;
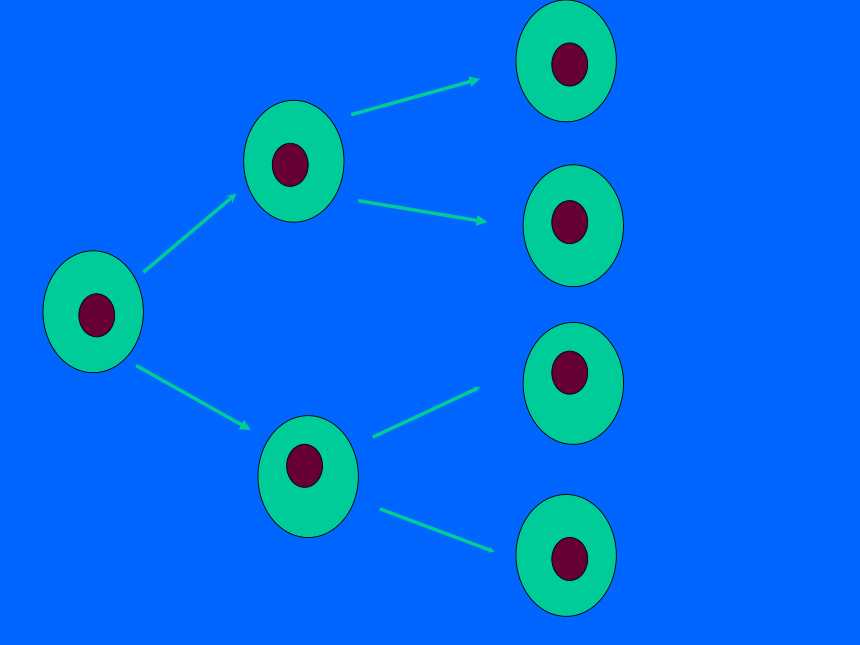
5、(-1)×(-1)×(-1)×(-1)×(-1)= 。-8120-14×4×4 某种细胞每30分钟便由一个分裂成两个.经过3小时这种细胞由1个能分裂成多少个?分裂方式如下所示:这个细胞分裂一次可得多少个细胞?那么,3小时共分裂了多少次?答:一次得:
两次 :
三次 :
2个;2×2个;2×2×2个; 六次 : 2×2×2×2×2×2个.分裂两次呢?分裂三次呢?请比较正方体的体积值式子:
4×4×4和细胞分裂六次后的个数式子: 2×2×2×2×2×2.它们有什么相同点?答:它们都是乘法;并且,它们各自的因数都相同.这样的运算我们叫作
乘方运算.
乘方:求相同因数积的运算.4×4×4记作: 2 ×2×2×2×2×2记作: 一般的,任意多个相同的有理数相乘,我们通常记作:4326 (因数)(因数的个数)其中a代表相乘的因数,n代表
相乘因数的个数即:an=口答练习一
1)在 中,12是 数,10是
数,读作 ;
2) 的底数是 ,指数是 ,读作 ;
7的7次方底指12的10次方 3)在 中,-3是 数,16是 数,读作 ; 4)在 中,底数是 ;指数是 ;读作 ;底指-3的16次方17 的17次方
5)5看成幂的话,底数是 ,指数是 ,可读作 ; 6) 看成幂的话,底数是 ,指数是 ,可读作 ;515的一次方1的一次方
练习二
一、把下列乘法式子写成乘方的形式:
1、1×1×1×1×1×1×1= ;
2、3×3×3×3×3= ;
3、(-3)×(-3)×(-3)×(-3)= ;
4、 = ;
二、把下列乘方写成乘法的形式:
1、 = ;
2、 = ;
3、 = ;
思考:用乘方式子怎么表示 的相反数?练习三
判断下列各题是否正确:
( )① ;
( )② ;
( )③ ;
( )④对错错错例1 计算:
(1)5 3 (2) (-3)4(3)解:(1) 53 = 5×5×5=125; (2) =(-3)·(-3) ·(-3) ·(-3)=81.(3)=(-1/2) (-1/2) (-1/2) =-1/8.例2 计算:
(1)102 103 104 (2)
注意:当底数是负数或分数时,底数一定要加上括号,这也是辩认底数的方法.解(1)102 =10×10103 ==1000;104 =(2)(-10)2=(-10)×(-10)=(-10)3==-1000;(-10)4==1000010 ×10×10×10=10000;100(-10)×(-10)×(-10)(-10)×(-10)×(-10)×(-10)10 ×10×10=100;观察例2的结果,你能发现什么规律?答:10的几次方,1后面就有几
个0;
想一想:把底数10换成0.1会怎么样呢?你还能发现什么规律?答:正数的任何次幂还是正数;而负数的奇次幂是负数;偶次幂是正数.这节课你学到了什么?乘方的故事 有一个长工到一个财主家去做工,他和财主商定:“第一天给一分钱,第二天给两分钱,以后每天是前一天的平方.”财主答应了,到月底(30天)后,你猜一猜:财主会给长工多少钱? 月底,长工兴冲冲的去领钱,他以为自己一下子可以领到一笔天文财富,结果财主只给了长工5分钱,而且还说是多给了他.长工算法:
第一天1分,第二天2分,第三天4分,第四天16分,第五天256分……财主算法:
第一天0.01元,第二天0.02元,第三天0.0004元,第四天0.00000016元……再见
1、边长为 的正方形的面积为 ;
2、棱长为 的正方体的体积为 ;
3、(-2)×(-2)×(-2)= ;
4、(-1)×(-2)×(-3)×(-4)×5= ;
5、(-1)×(-1)×(-1)×(-1)×(-1)= 。-8120-14×4×4 某种细胞每30分钟便由一个分裂成两个.经过3小时这种细胞由1个能分裂成多少个?分裂方式如下所示:这个细胞分裂一次可得多少个细胞?那么,3小时共分裂了多少次?答:一次得:
两次 :
三次 :
2个;2×2个;2×2×2个; 六次 : 2×2×2×2×2×2个.分裂两次呢?分裂三次呢?请比较正方体的体积值式子:
4×4×4和细胞分裂六次后的个数式子: 2×2×2×2×2×2.它们有什么相同点?答:它们都是乘法;并且,它们各自的因数都相同.这样的运算我们叫作
乘方运算.
乘方:求相同因数积的运算.4×4×4记作: 2 ×2×2×2×2×2记作: 一般的,任意多个相同的有理数相乘,我们通常记作:4326 (因数)(因数的个数)其中a代表相乘的因数,n代表
相乘因数的个数即:an=口答练习一
1)在 中,12是 数,10是
数,读作 ;
2) 的底数是 ,指数是 ,读作 ;
7的7次方底指12的10次方 3)在 中,-3是 数,16是 数,读作 ; 4)在 中,底数是 ;指数是 ;读作 ;底指-3的16次方17 的17次方
5)5看成幂的话,底数是 ,指数是 ,可读作 ; 6) 看成幂的话,底数是 ,指数是 ,可读作 ;515的一次方1的一次方
练习二
一、把下列乘法式子写成乘方的形式:
1、1×1×1×1×1×1×1= ;
2、3×3×3×3×3= ;
3、(-3)×(-3)×(-3)×(-3)= ;
4、 = ;
二、把下列乘方写成乘法的形式:
1、 = ;
2、 = ;
3、 = ;
思考:用乘方式子怎么表示 的相反数?练习三
判断下列各题是否正确:
( )① ;
( )② ;
( )③ ;
( )④对错错错例1 计算:
(1)5 3 (2) (-3)4(3)解:(1) 53 = 5×5×5=125; (2) =(-3)·(-3) ·(-3) ·(-3)=81.(3)=(-1/2) (-1/2) (-1/2) =-1/8.例2 计算:
(1)102 103 104 (2)
注意:当底数是负数或分数时,底数一定要加上括号,这也是辩认底数的方法.解(1)102 =10×10103 ==1000;104 =(2)(-10)2=(-10)×(-10)=(-10)3==-1000;(-10)4==1000010 ×10×10×10=10000;100(-10)×(-10)×(-10)(-10)×(-10)×(-10)×(-10)10 ×10×10=100;观察例2的结果,你能发现什么规律?答:10的几次方,1后面就有几
个0;
想一想:把底数10换成0.1会怎么样呢?你还能发现什么规律?答:正数的任何次幂还是正数;而负数的奇次幂是负数;偶次幂是正数.这节课你学到了什么?乘方的故事 有一个长工到一个财主家去做工,他和财主商定:“第一天给一分钱,第二天给两分钱,以后每天是前一天的平方.”财主答应了,到月底(30天)后,你猜一猜:财主会给长工多少钱? 月底,长工兴冲冲的去领钱,他以为自己一下子可以领到一笔天文财富,结果财主只给了长工5分钱,而且还说是多给了他.长工算法:
第一天1分,第二天2分,第三天4分,第四天16分,第五天256分……财主算法:
第一天0.01元,第二天0.02元,第三天0.0004元,第四天0.00000016元……再见
