余角和补角

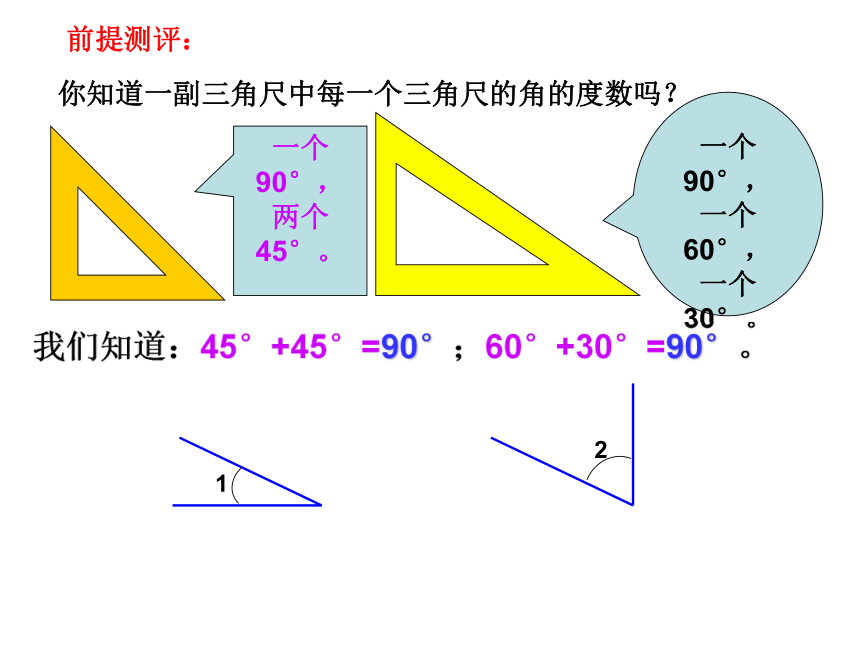
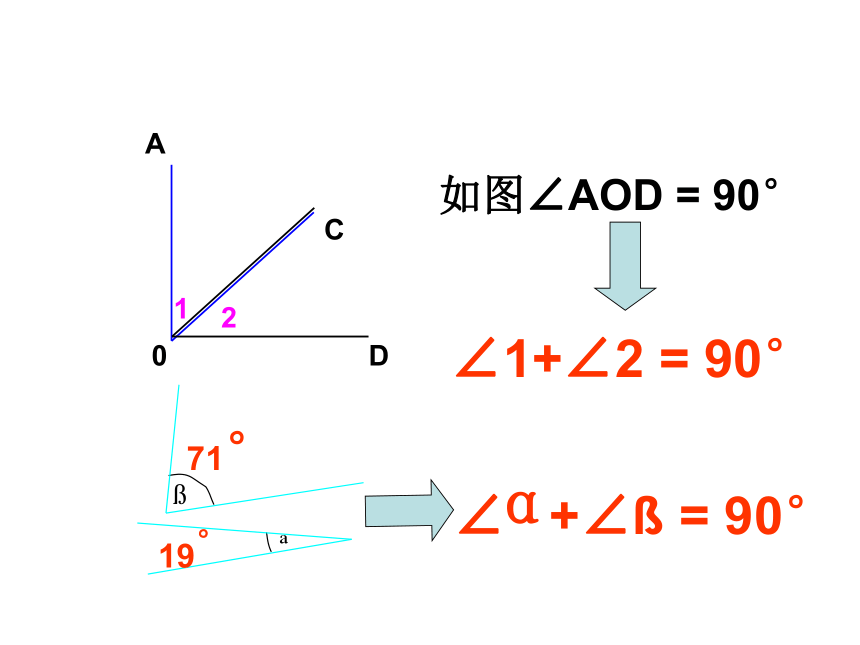
课件32张PPT。 4.3.3余角和补角你知道一副三角尺中每一个三角尺的角的度数吗？一个90°，两个45°。一个90°，一个60°，一个30°。我们知道：45°+45°=90°；60°+30°=90°。前提测评：如图∠AOD = 90°∠1+∠2 = 90° 两个角的和等于90°（直角），
就说这两个角互为余角，简称互余。练一练：
1、如图 ∠1+∠2=90°，
⑴∠1与∠2互为 ；
⑵∠1的余角是 ；
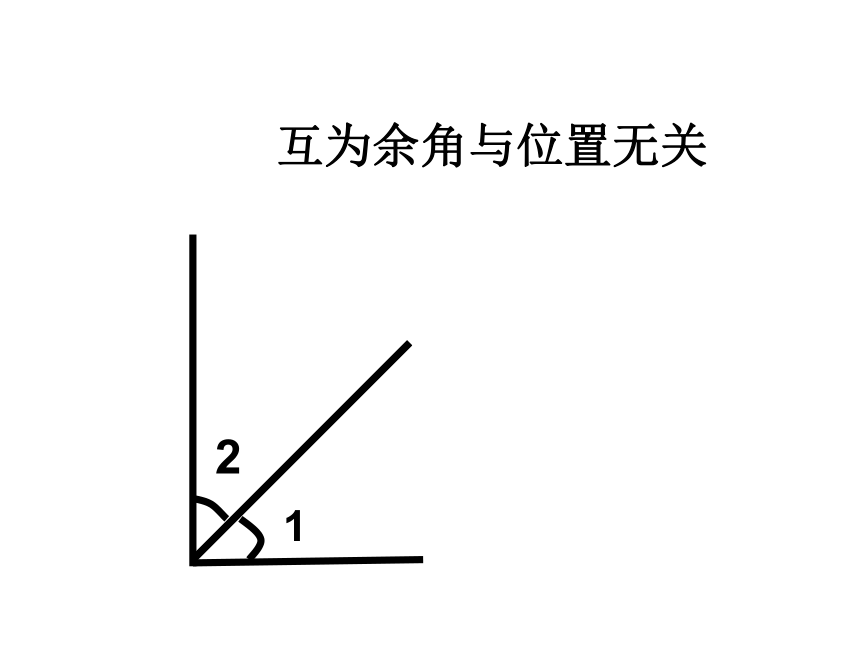
⑶∠1是 的余角。如果∠1+∠2=90°，那么∠1与∠2互为余角余角∠2∠2即其中一个角是另一个角的余角。2
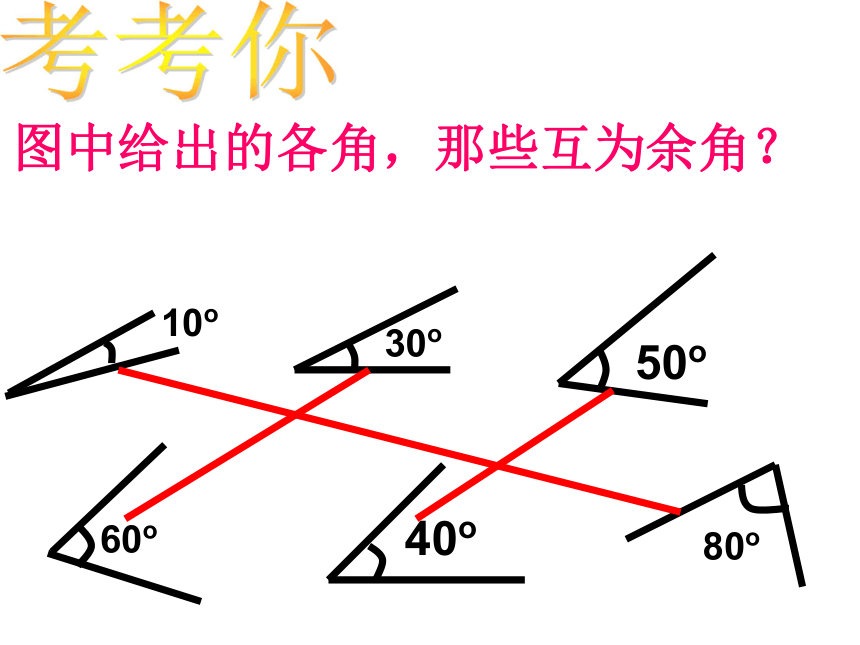
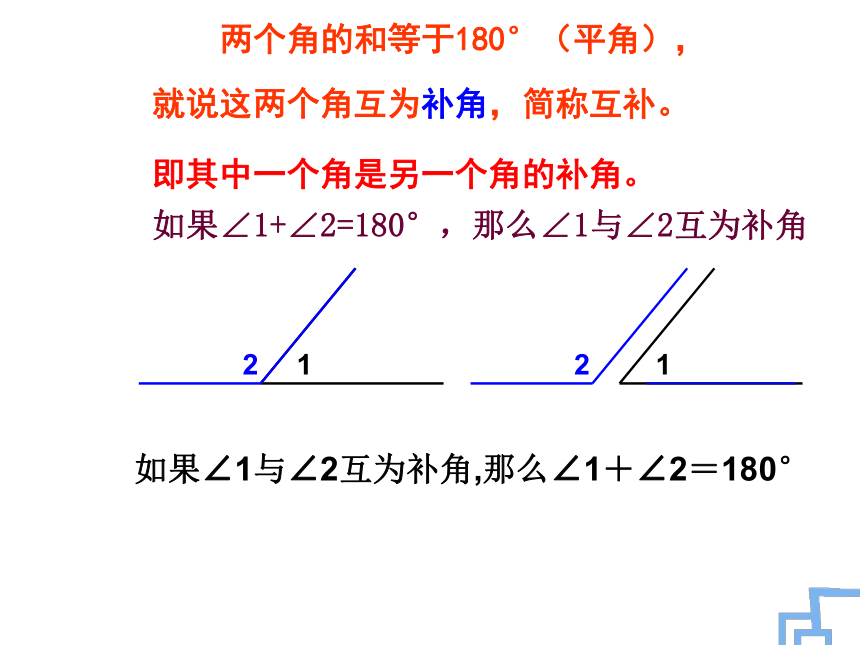
1互为余角与位置无关考考你图中给出的各角，那些互为余角？10o30o60o80o50o40o 两个角的和等于180°（平角），
就说这两个角互为补角，简称互补。
即其中一个角是另一个角的补角。
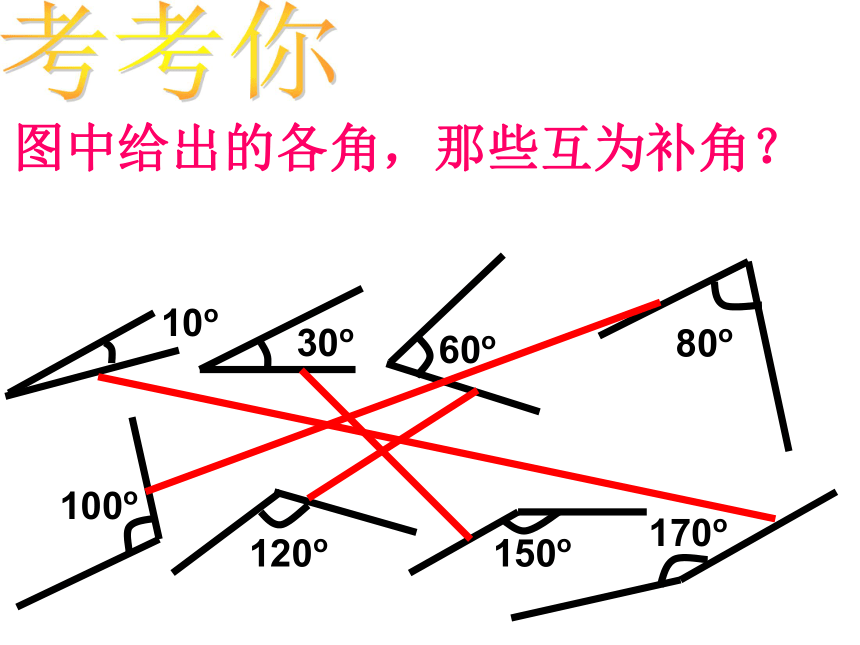
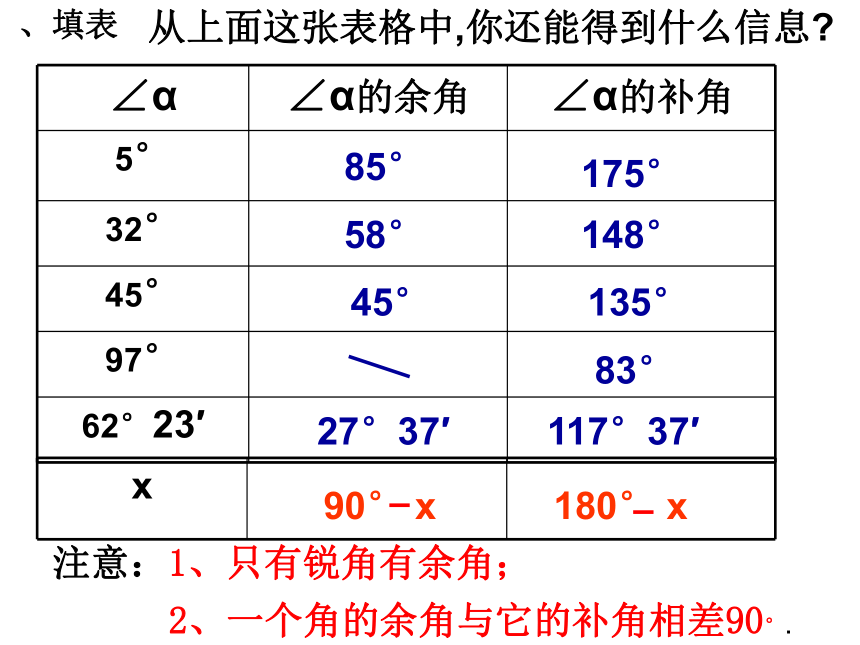
如果∠1与∠2互为补角,那么∠1＋∠2＝180°1如果∠1+∠2=180°，那么∠1与∠2互为补角34互为补角与位置无关考考你图中给出的各角，那些互为补角？10o30o60o80o100o120o150o170o 、填表27°37′117°37′85°175°58°148°45°135°83°从上面这张表格中,你还能得到什么信息?注意：1、只有锐角有余角；
2、一个角的余角与它的补角相差90°.（3）如果一个角的余角和补角都存在，那么这
个角的余角一定比这个角的补角小.（2）如果两个角互补，那么这两个角中，一个
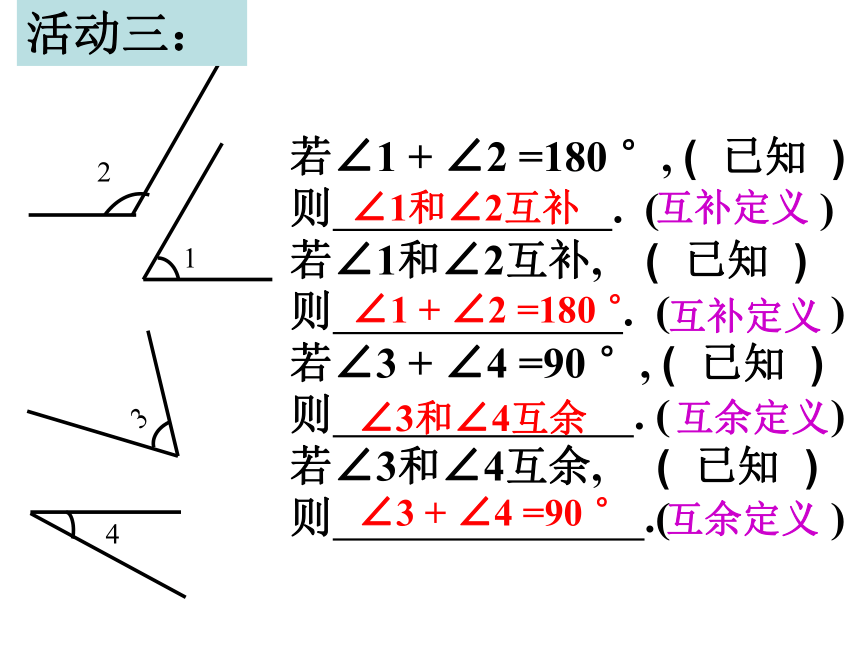
是锐角，另一个是钝角；（1）一个锐角的补角一定是钝角； 、判断下列说法是否正确，并说明理由.√√若∠1 + ∠2 =180 °, ( 已知 )
则 . ( )
若∠1和∠2互补, ( 已知 )
则 . ( )
若∠3 + ∠4 =90 °, ( 已知 )则 . ( )
若∠3和∠4互余, ( 已知 )
则 .( )312∠1和∠2互补互补定义∠1 + ∠2 =180 °互补定义∠3和∠4互余互余定义∠3 + ∠4 =90 °互余定义活动三：问题3：互为余角、互为补角的两个角是否一定有公共顶点？ 问题1：以上定义中的“互为”是什么意思？∠COD∠DOB∠AOD∠1+ ∠2 = 90 °∠1+ ∠2 = 180 °同角或等角的余角相等。同角或等角的补角相等。注意:互余、互补是指两个角的数量关系，与位置无关理一理 ：　　　
如图∠1 与∠2互补，∠３ 与∠４互补 ，如果∠1＝∠３,那么∠2与∠４相等吗？为什么？
2143（ ）（ ）探究:余角和补角的性质探究:补角的性质解：∵ ∠1 +∠2=180°， ∠3 +∠4=180°∴ ∠2=180°－∠1 ， ∠4=180°－ ∠3∵ ∠1 =∠3∴ 180°－∠1 =180°－ ∠3即：∠2 =∠4　 如图∠1 与∠2互补，∠３ 与∠４互补 ，如果∠1＝∠３,那么∠2与∠４相等吗？为什么？ 例3 如图，∠1与∠2互补，∠3与∠4互补，如果∠1=∠3，那么∠2与∠4相等吗？为什么?解：∠2与∠4相等。因为∠1与∠2互补；∠3与∠4互补，所以∠2=180°-∠1；∠4=180°-∠3，
所以∠1+∠2 = 180° ； ∠3+∠4 = 180°，
所以∠2=∠4。
又因为∠1=∠3，　如图∠1 与∠2互余，∠３ 与∠４互余 ，如果∠1＝∠３，那么∠2与∠４相等吗？为什么？1
2
43探究:余角和补角的性质（ ）（ ）　如图∠1 与∠2互余，∠３ 与∠４互余 ，如果∠1＝∠３，那么∠2与∠４相等吗？为什么？1
2
43解：∠2与∠4相等。因为∠1与∠2互余；∠3与∠4互余，所以∠1+∠2 = 90° ； ∠3+∠4 = 90°， 所以∠2=90°-∠1；∠4=90°-∠3，
又因为∠1=∠3，
所以∠2=∠4。
补角性质：
同角或等角的补角相等
余角性质
同角或等角的余角相等
如图∠AOB = 90 °
∠COD = 90 °
则∠1与∠2是什么关系？答： ∠1 = ∠2
因为∠1+ ∠BOD = 90 °
∠2+ ∠BOD = 90 °
所以∠1 = ∠2AOBCD（同角的余角相等)12同角或等角的补角相等同角或等角的余角相等.　如图,∠AOB=90°,∠COD=∠EOD=90°,C,O,E在一条直线上,且∠2=∠4,请说出∠1与∠3之间的关系？并试着说明理由？已知，点A,O,B在同一直线上，OE,OF分别为∠AOC和∠BOC的角平分线，找图中互余和互补的角。
动动脑例1
若一个角的补角等于它的余角的4倍，求这个角的度数。解：设这个角是x °，则它的补角是（180-x） °,余角是(90-x) ° 。
根据题意得:（180-x） °= 4 (90-x) °
解得： x =60
答：这个角的度数是60 °。你能想出方法吗？
解： 设这个角的度数为x度，由题意得：请你试一试已知：一个锐角的补角加上20°后等于这角的3倍。
求：这个角的度数答：这个角为50°。 有时以正北、正南方向为基准，描述物体运动的方向. 表示方向的角（方位角）在航行、测绘等工作中经常用到.推导性质，理解运用例１　如图，ＯＡ是表示北偏东３００方向的一条射线，仿照
这条射线，画出表示下列方向的角：
（１）南偏东２５０　　　　（２）北偏西６００ 例2 如图，货轮O在航行过程中，发现灯塔A在南偏东60°的方向上。同时，在它北偏东40°、南偏西10°、西北方向上又分别发现了客轮B、货轮C和海岛D.仿照表示灯塔方位的方法，画出表示客轮B、货轮C和海岛D的射线。3、A看B的方向是北偏东30°，那么B看A的方向是（ ）
（A）南偏东60°（B）南偏西60°
（C）南偏东30° （D）南偏西30° 如图，A地和B地都是海上观测站，从A地发现它的北偏东60°方向有一艘船，同时，从B地发现这艘船在它北偏东30°方向，试在图中确定这艘船的位置。··C解：如图所示，这艘船的位置在点C处。 ● 本节课你学到了哪些知识？ ● 通过这节课的学习后,你有什么感受? BYE-BYE!