有理数的乘方[上学期]
图片预览






文档简介
课件21张PPT。
有理数的乘方 口答:
1. (-2) ×(-2) ×(-2)
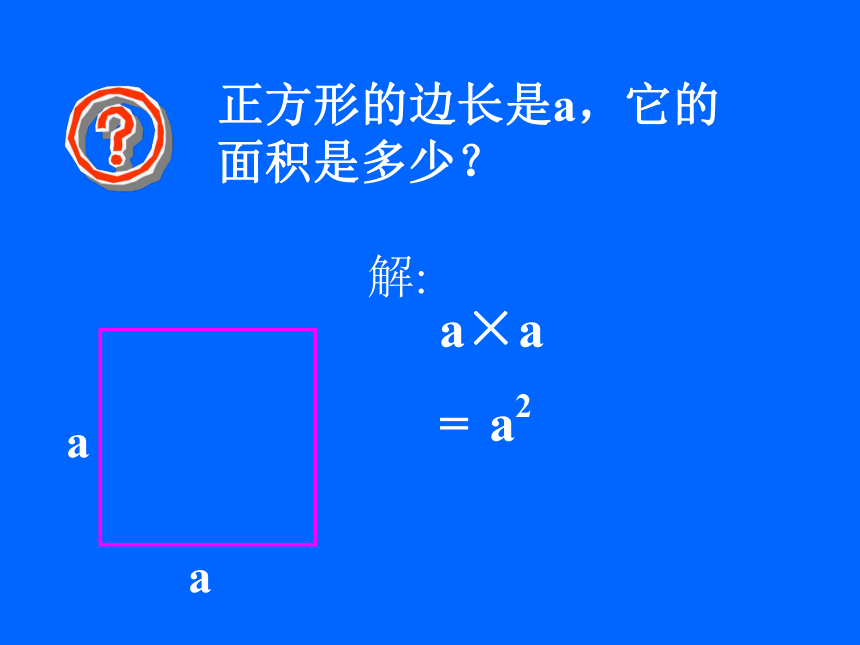
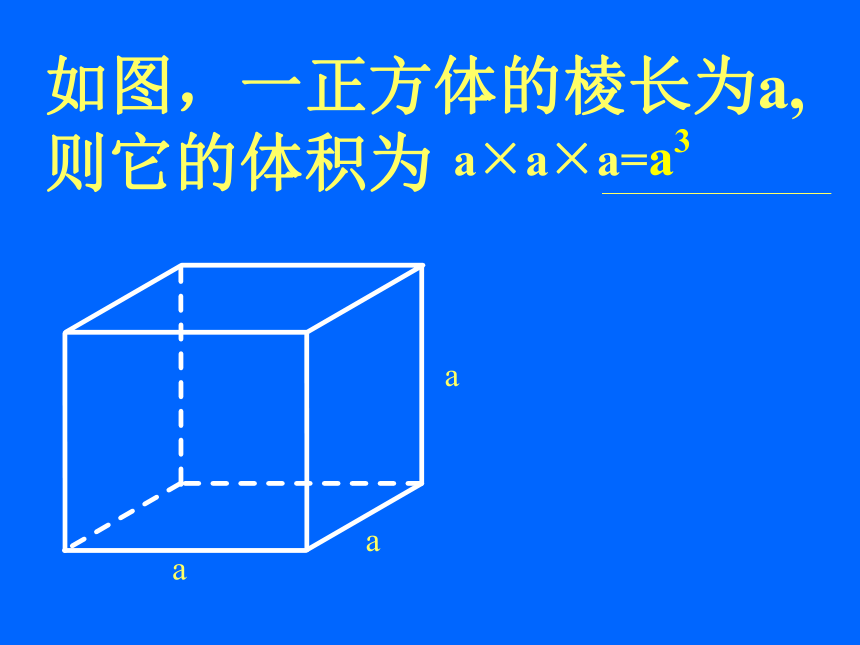
3. (-2) × (-2) ×(-2) ×(-2) ×(-2) 2.-8-32观察以上各式有什么共同特点:答:它们都是乘法;并且,它们各自的因数都相同.正方形的边长是a,它的面积是多少?解:a×aa2=a×a×a=a3
这样的运算我们叫作
乘方运算.
乘方:求相同因数积的运算.4×4×4记作:
2 ×2×2×2×2×2记作:
一般的,任意多个相同的有理数相乘,我们规定:4326例如:a×a×a记作: a3
其中a代表相乘的因数,n代表
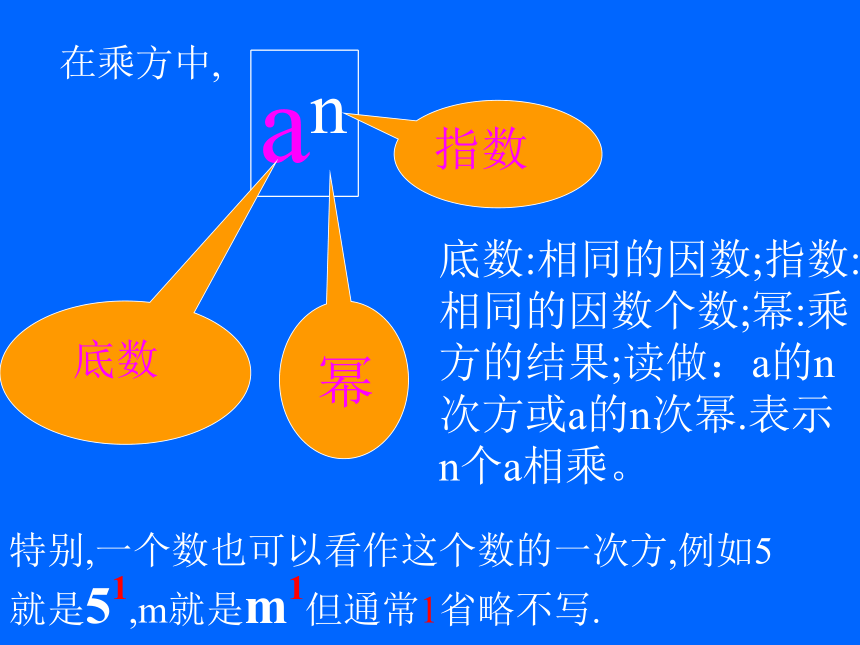
相乘因数的个数即:an=在乘方中,
指数
底数幂底数:相同的因数;指数:相同的因数个数;幂:乘方的结果;读做:a的n次方或a的n次幂.表示n个a相乘。特别,一个数也可以看作这个数的一次方,例如5就是51,m就是m1但通常1省略不写.
思 考 (-2)×(-2)×(-2)×(-2)×(-2) 可记作 (-2)5(+ ) ×(+ ) ×(+ ) ×(+ )可记作(+ )4 × × × 可记作+ 的几次方? (-2)×(-2)×(-2)×(-2)×(-2)可记作-2的几次方?讨论: 乘方与乘法的异同乘法乘法一定相同不一定相同幂积 例1 计算:
(1)5 3 (2) (-3)4(3)解:(1)53 =
5×5×5=125; (2) =(-3)·(-3) ·(-3) ·(-3)
=81.(3)=(-1/2) (-1/2) (-1/2) =-1/8.例2 计算:
(1)102 103 104 (2)
注意:当底数是负数或分数时,底数一定要加上括弧,这
也是辩认底数的方法.解:(1)102
=10×10=100;103 =10 ×10×10
=1000;104 =10 ×10×10
×10=10000;(2)(-10)2 =(-10)×(-10)=100(-10)3 =(-10)× (-10) × (-10)=-1000;(-10)4 =(-10) × (-10) × (-10)
× (-10)=10000。观察例2的结果,你能发现什么规律?答:10的几次方,1后面就有几
个0;
想一想:你还能发现什么规律乘方运算的符号法则:(1) 正数的任何次幂是……(2) 负数的奇数次幂是……负数的偶数次幂是……正数负数正数(3) 0的任何正整数次幂都是0练习:判断下列各幂是正的还是负的。(1) (-7)9(2) (-3)6(3) (-1)101 负 负 正 负 正 (5) -(-2)4负 (6) (4) 练习:计算并注意他们的区别
1)2*(– 3)= 2)(–3)2 =
3)2*32 = 4)(2*3)2=
5)32 = 6)23 =
7) – 34 = 8)(– 3)4 =
9)22/3 = 10)(2/3)2 =特别,7)表示3的4次方的相反数,而8)表示的是(– 3)的4次方,运算顺序完全不同,结果也不相同.
-6189-814/39368814/9(1) 有理数乘方的意义(2) 乘方是一种运算,幂是乘方的结果(3) 乘方运算的符号法则课堂小结:是非题:(1) (-4)2= -42……………(2) 32= 3 × 2……………(3) 32= 23………………(4) (-2)3= 8………………××××
有理数的乘方 口答:
1. (-2) ×(-2) ×(-2)
3. (-2) × (-2) ×(-2) ×(-2) ×(-2) 2.-8-32观察以上各式有什么共同特点:答:它们都是乘法;并且,它们各自的因数都相同.正方形的边长是a,它的面积是多少?解:a×aa2=a×a×a=a3
这样的运算我们叫作
乘方运算.
乘方:求相同因数积的运算.4×4×4记作:
2 ×2×2×2×2×2记作:
一般的,任意多个相同的有理数相乘,我们规定:4326例如:a×a×a记作: a3
其中a代表相乘的因数,n代表
相乘因数的个数即:an=在乘方中,
指数
底数幂底数:相同的因数;指数:相同的因数个数;幂:乘方的结果;读做:a的n次方或a的n次幂.表示n个a相乘。特别,一个数也可以看作这个数的一次方,例如5就是51,m就是m1但通常1省略不写.
思 考 (-2)×(-2)×(-2)×(-2)×(-2) 可记作 (-2)5(+ ) ×(+ ) ×(+ ) ×(+ )可记作(+ )4 × × × 可记作+ 的几次方? (-2)×(-2)×(-2)×(-2)×(-2)可记作-2的几次方?讨论: 乘方与乘法的异同乘法乘法一定相同不一定相同幂积 例1 计算:
(1)5 3 (2) (-3)4(3)解:(1)53 =
5×5×5=125; (2) =(-3)·(-3) ·(-3) ·(-3)
=81.(3)=(-1/2) (-1/2) (-1/2) =-1/8.例2 计算:
(1)102 103 104 (2)
注意:当底数是负数或分数时,底数一定要加上括弧,这
也是辩认底数的方法.解:(1)102
=10×10=100;103 =10 ×10×10
=1000;104 =10 ×10×10
×10=10000;(2)(-10)2 =(-10)×(-10)=100(-10)3 =(-10)× (-10) × (-10)=-1000;(-10)4 =(-10) × (-10) × (-10)
× (-10)=10000。观察例2的结果,你能发现什么规律?答:10的几次方,1后面就有几
个0;
想一想:你还能发现什么规律乘方运算的符号法则:(1) 正数的任何次幂是……(2) 负数的奇数次幂是……负数的偶数次幂是……正数负数正数(3) 0的任何正整数次幂都是0练习:判断下列各幂是正的还是负的。(1) (-7)9(2) (-3)6(3) (-1)101 负 负 正 负 正 (5) -(-2)4负 (6) (4) 练习:计算并注意他们的区别
1)2*(– 3)= 2)(–3)2 =
3)2*32 = 4)(2*3)2=
5)32 = 6)23 =
7) – 34 = 8)(– 3)4 =
9)22/3 = 10)(2/3)2 =特别,7)表示3的4次方的相反数,而8)表示的是(– 3)的4次方,运算顺序完全不同,结果也不相同.
-6189-814/39368814/9(1) 有理数乘方的意义(2) 乘方是一种运算,幂是乘方的结果(3) 乘方运算的符号法则课堂小结:是非题:(1) (-4)2= -42……………(2) 32= 3 × 2……………(3) 32= 23………………(4) (-2)3= 8………………××××
