1.5.2科学记数法 课件(共32张PPT)
文档属性
| 名称 | 1.5.2科学记数法 课件(共32张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-09 00:00:00 | ||
图片预览










文档简介
(共32张PPT)
人教版 七年级上册
1.5.2 科学记数法
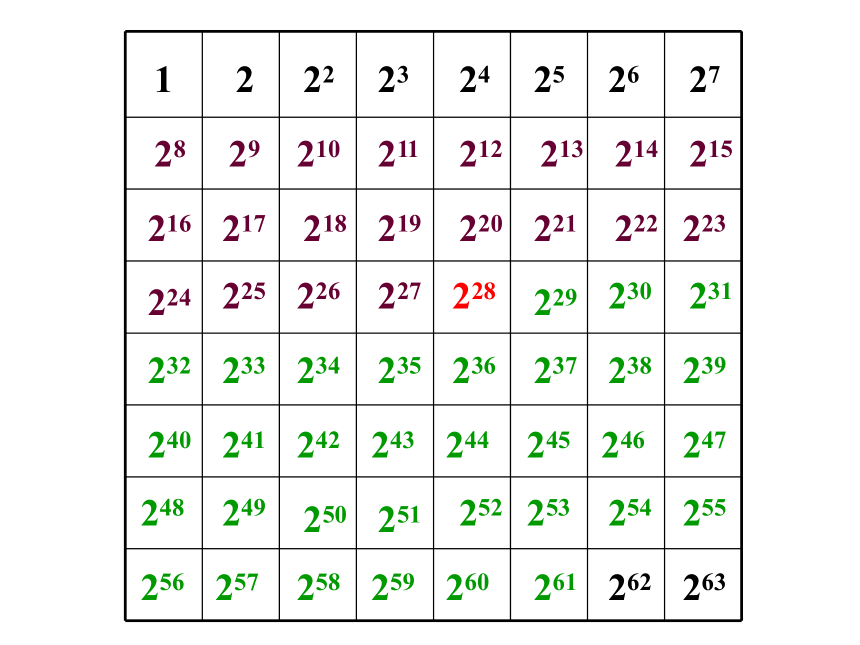
传说西塔创造了国际象棋而使国王非常快乐,他决议要重赏西塔,西塔说:“本人不要你的重赏,陛下,只需你在本人的棋盘上赏一些麦子就行了。在棋盘的第1个格子里放1粒,在第2个格子里放2粒,在第3个格子里放4粒,在第4个格子里放8粒,依此类推,以后每一个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍,直到放满第64个格子就行了”.区区小数,几粒麦子,这有何难,“来人”,国王令人如数付给西塔.
讲故事 引入新课
1
2
22
23
24
25
26
27
28
29
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
1+22+23
+263
=
+…+262
264
=
18 446 744 073 709 551 616
粒麦子终究有多少?打个比如,假如造一个仓库来放这些麦子,仓库高4公尺,宽10公尺,那么仓库的长度就等于地球到太阳的之间的两倍。而要消费这么多的麦子,全世界要两千年.虽然国王十分富有,但要这样多的麦子他是怎样也拿不出来的.
-1
18 446 744 073 709 551 615
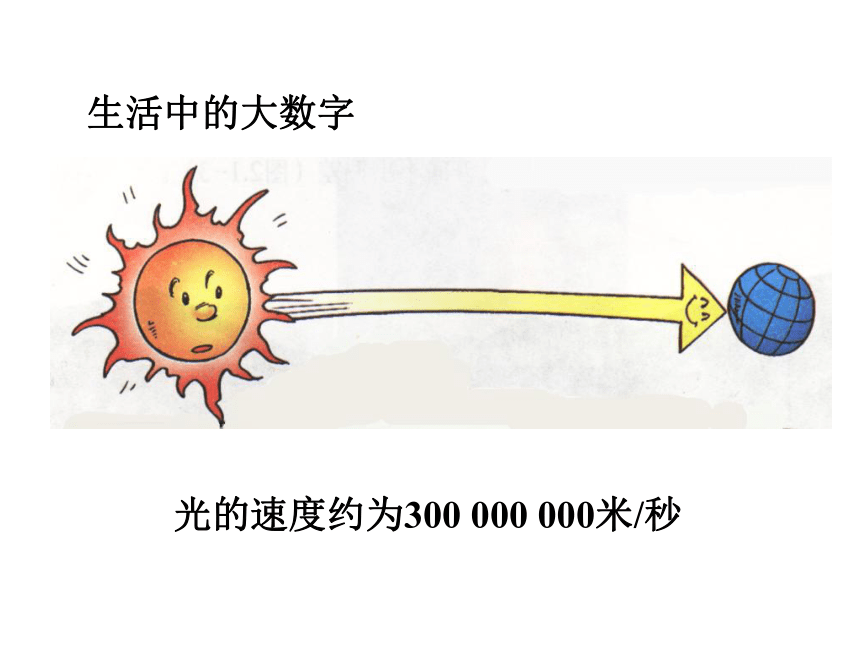
太阳的半径约为696 000 千米
生活中的大数字
光的速度约为300 000 000米/秒
生活中的大数字
世界总人口数约为
7 000 000 000人.
生活中的大数字
注意这些数据
696 000
300 000 000
700 000 000
18 446 744 073 709 551 615
···
有简单的表示方法吗?
102 = ;
104=_________;
105= ;
103= ;
1010= ;
10n= ;
100
1 000
10 000
100 000
10 000 000 000
1000 ··· 0(n个0)
以10为底的幂的0的个数与指数有相等关系。
所以就可以用10的乘方表示一些大数.
以10为底的幂的0的个数与指数有何关系?
学习新知
(1)1000
(2)1000000
(3)100000000
=103
把下列各数写成10的幂的形式.
=106
=108
学以致用
下面这些大数应该怎样表示?
(1)567 000 000;
(2)22 600 000 000;
(3)6 100 000 000.
学习新知
书写简短,便于读数.
读作:5.67乘10的8次方(幂)
解:567 000 000
22 600 000 000 =
6 100 000 000=
=6.1×
10 000 000 000
2.26×
= 2.26×
1 000 000 000
109
6.1×
100 000 000
=5.67×
=5.67×
108
1010
像这样,把一个大于10的数表示成 a×10n(其中a大于或等于1且小于10, n为正整数),使用的是科学记数法.
22 600 000 000= 2.26×1010
567 000 000= 5.67×108
6 100 000 000= 6.1×1010
学习新知
1400 000=1.4×___; 300 000=3×____;
14 000=1.4× ___; 1460=1.46×___;
147=1.47×___.
106
105
104
103
102
1.填空:
练习巩固
用科学记数法表示一个数时,10的指数n与原数的整数位数有什么关系?
10的指数比原数的整数位数少1.
2.下列各数是否是用科学记数法表示的?
不是
不是
2 400 000= 0.24×107
2 400 000= 2.4×106
30 000 000= 30×106
30 000 000= 3×107
是
是
例5. 用科学记数法表示下列各数:
①1 000 000,②57 000 000,③-123 000 000 000.
解:
例题解析
①
因为1 000 000是七位整数,
所以a=1,
n=7-1=6,
所以1 000 000=1×106;
②
因为57 000 000是八位整数,
所以a=5.7,
n=8-1=7,
所以57 000 000=5.7×107;
③
因为-123 000 000是12位整数,
所以a=-1.23,
n=12-1=11,
所以-123 000 000=-1.23×1011.
练习:用科学记数法表示下列各数:
10 000 000 000,453 000 000 ,
56 900 000 000,-2 360 000 000 000.
解:
10 000 000 000=1010;
453 000 000=4.53×108;
56 900 000 000=5.69×1010;
-2 360 000 000 000=-2.36×1012.
下列用科学记数法写出的数,原来分别是什么数?
①1.5×106, ②2. 34×105, ③-1. 27×105.
例题解析
因为10的指数为6,
所以原数的整数部分
有7位,
把1.5的小数点向右移动6位,
①
解:
得原数
为1 500 000;
②
因为10的指数为5,
所以原数的整数部分
有6位,
把2.34的小数点向右移动5位,
得原数
为234 000;
下列用科学记数法写出的数,原来分别是什么数?
①1.5×106, ②2. 34×105, ③-1. 27×105.
例题解析
因为10的指数为5,
所以原数的整数部分
有6位,
把-1.27的小数点向右移动5位,
解:
得原数为-1 27 000.
③
技巧:10的指数是几,小数点就向后移动几位.
10 000
800 000
56 000 000
-7 400 000
练一练
1.用科学记数法写出下列各数:
10 000, 800 000, 56 000 000, -7 400 000.
=104
=8×105
=5.6×107
=-7.4×106
解:
1×107
4×103
8.5×106
7.04×105
-3.96×104
2.下列用科学记数法写出的数,原来分别是什么数?
1×107 , 4×103 , 8.5×106 ,
7.04×105 , -3.96×104 .
=10 000 000
=4 000
=8 500 000
=704 000
= -39600
解:
3.中国的陆地面积约为 9 600 000km2, 领水面积约为 370 000 km2,用科学记数法表示上述两个数字.
9 600 000
370 000
解:
=9.6×106
=3.7×105
解:因为1 年=365 天=365×24×60 分,
所以一年心跳次数约为:
365×24×60×70=
=3.679 2×107(次);
108÷( 3.6792×107 )
≈2.7(年),
因为心跳达到1亿次需要的时间是:
所以一个正常人一生心跳次数能达到1亿次.
36 792 000
4.一个正常人的平均心跳约为每分70次,一年(365天)大约跳几次 用科学记数法表示这个结果.一个正常人一生心跳次数能达到1亿次吗
5.我国是一个严重缺水国家,大家应珍惜水资源,节约用水.据测试,拧不紧的水龙头每秒钟会滴下2滴水,每滴水约0.05毫升.小明在洗手后,没有把水龙头拧紧,当他离开5小时后才被人发现并把水龙头拧紧,你能算出这期间浪费了多少毫升水吗?(结果用科学记数法表示)
解:5×3600×2×0.05=1800=1.8×103(毫升)
答:这期间浪费了1.8×103毫升水.
6.把2 230 000 000用科学记数法写成
2.23×10n-2的形式,求n 的值.
解:因为2 230 000 000
=2.23×109
所以n-2=9
所以n=11.
1.用科学记数法来表示大数
一般形式: a×10n( 1≤a<10,n为正整数)
2.用科学记数法表示大数的好处
3.用科学记数法a×10n表示大数关键要注意
两点:
(1)1≤a<10;
(2)当大数是大于10的整数时,n为整数位数减去1.
课堂小结:
2.若一个数用科学记数法表示为2.4×1021,则
这个数的整数部分的位数是( ).
A. 20 B.21 C.22 D.23
1.78 900 000用科学记数法表示为 ( ).
A. 789×105 B.0.789×109
C.7.89×107 D.7.89×108
巩固提高
C
C
3. 5.17×10n+1为用科学记数法表示的数,则
这个数的整数部分的位数是( ).
A. n-1 B.n C.n+1 D.n+2
D
4.若9 420 000用科学记数法表示为9.42×10n,
则n= .
6
5.若31 400 000用科学记数法表示a×10n,则
a= .
3.14
6.将0.05 ×105用科学记数法表示,则
0.05= .
5 ×103
7.已知一天有8.64 ×104秒若一年按365天计算,
则一年有 秒.(用科学记数法表示)
3.1536 ×107
8.64×104×365
=3153.6 ×104
=31 536 000
=3.1536 ×107
今天作业
课本第47页习题1.5第4、5题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 七年级上册
1.5.2 科学记数法
传说西塔创造了国际象棋而使国王非常快乐,他决议要重赏西塔,西塔说:“本人不要你的重赏,陛下,只需你在本人的棋盘上赏一些麦子就行了。在棋盘的第1个格子里放1粒,在第2个格子里放2粒,在第3个格子里放4粒,在第4个格子里放8粒,依此类推,以后每一个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍,直到放满第64个格子就行了”.区区小数,几粒麦子,这有何难,“来人”,国王令人如数付给西塔.
讲故事 引入新课
1
2
22
23
24
25
26
27
28
29
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
1+22+23
+263
=
+…+262
264
=
18 446 744 073 709 551 616
粒麦子终究有多少?打个比如,假如造一个仓库来放这些麦子,仓库高4公尺,宽10公尺,那么仓库的长度就等于地球到太阳的之间的两倍。而要消费这么多的麦子,全世界要两千年.虽然国王十分富有,但要这样多的麦子他是怎样也拿不出来的.
-1
18 446 744 073 709 551 615
太阳的半径约为696 000 千米
生活中的大数字
光的速度约为300 000 000米/秒
生活中的大数字
世界总人口数约为
7 000 000 000人.
生活中的大数字
注意这些数据
696 000
300 000 000
700 000 000
18 446 744 073 709 551 615
···
有简单的表示方法吗?
102 = ;
104=_________;
105= ;
103= ;
1010= ;
10n= ;
100
1 000
10 000
100 000
10 000 000 000
1000 ··· 0(n个0)
以10为底的幂的0的个数与指数有相等关系。
所以就可以用10的乘方表示一些大数.
以10为底的幂的0的个数与指数有何关系?
学习新知
(1)1000
(2)1000000
(3)100000000
=103
把下列各数写成10的幂的形式.
=106
=108
学以致用
下面这些大数应该怎样表示?
(1)567 000 000;
(2)22 600 000 000;
(3)6 100 000 000.
学习新知
书写简短,便于读数.
读作:5.67乘10的8次方(幂)
解:567 000 000
22 600 000 000 =
6 100 000 000=
=6.1×
10 000 000 000
2.26×
= 2.26×
1 000 000 000
109
6.1×
100 000 000
=5.67×
=5.67×
108
1010
像这样,把一个大于10的数表示成 a×10n(其中a大于或等于1且小于10, n为正整数),使用的是科学记数法.
22 600 000 000= 2.26×1010
567 000 000= 5.67×108
6 100 000 000= 6.1×1010
学习新知
1400 000=1.4×___; 300 000=3×____;
14 000=1.4× ___; 1460=1.46×___;
147=1.47×___.
106
105
104
103
102
1.填空:
练习巩固
用科学记数法表示一个数时,10的指数n与原数的整数位数有什么关系?
10的指数比原数的整数位数少1.
2.下列各数是否是用科学记数法表示的?
不是
不是
2 400 000= 0.24×107
2 400 000= 2.4×106
30 000 000= 30×106
30 000 000= 3×107
是
是
例5. 用科学记数法表示下列各数:
①1 000 000,②57 000 000,③-123 000 000 000.
解:
例题解析
①
因为1 000 000是七位整数,
所以a=1,
n=7-1=6,
所以1 000 000=1×106;
②
因为57 000 000是八位整数,
所以a=5.7,
n=8-1=7,
所以57 000 000=5.7×107;
③
因为-123 000 000是12位整数,
所以a=-1.23,
n=12-1=11,
所以-123 000 000=-1.23×1011.
练习:用科学记数法表示下列各数:
10 000 000 000,453 000 000 ,
56 900 000 000,-2 360 000 000 000.
解:
10 000 000 000=1010;
453 000 000=4.53×108;
56 900 000 000=5.69×1010;
-2 360 000 000 000=-2.36×1012.
下列用科学记数法写出的数,原来分别是什么数?
①1.5×106, ②2. 34×105, ③-1. 27×105.
例题解析
因为10的指数为6,
所以原数的整数部分
有7位,
把1.5的小数点向右移动6位,
①
解:
得原数
为1 500 000;
②
因为10的指数为5,
所以原数的整数部分
有6位,
把2.34的小数点向右移动5位,
得原数
为234 000;
下列用科学记数法写出的数,原来分别是什么数?
①1.5×106, ②2. 34×105, ③-1. 27×105.
例题解析
因为10的指数为5,
所以原数的整数部分
有6位,
把-1.27的小数点向右移动5位,
解:
得原数为-1 27 000.
③
技巧:10的指数是几,小数点就向后移动几位.
10 000
800 000
56 000 000
-7 400 000
练一练
1.用科学记数法写出下列各数:
10 000, 800 000, 56 000 000, -7 400 000.
=104
=8×105
=5.6×107
=-7.4×106
解:
1×107
4×103
8.5×106
7.04×105
-3.96×104
2.下列用科学记数法写出的数,原来分别是什么数?
1×107 , 4×103 , 8.5×106 ,
7.04×105 , -3.96×104 .
=10 000 000
=4 000
=8 500 000
=704 000
= -39600
解:
3.中国的陆地面积约为 9 600 000km2, 领水面积约为 370 000 km2,用科学记数法表示上述两个数字.
9 600 000
370 000
解:
=9.6×106
=3.7×105
解:因为1 年=365 天=365×24×60 分,
所以一年心跳次数约为:
365×24×60×70=
=3.679 2×107(次);
108÷( 3.6792×107 )
≈2.7(年),
因为心跳达到1亿次需要的时间是:
所以一个正常人一生心跳次数能达到1亿次.
36 792 000
4.一个正常人的平均心跳约为每分70次,一年(365天)大约跳几次 用科学记数法表示这个结果.一个正常人一生心跳次数能达到1亿次吗
5.我国是一个严重缺水国家,大家应珍惜水资源,节约用水.据测试,拧不紧的水龙头每秒钟会滴下2滴水,每滴水约0.05毫升.小明在洗手后,没有把水龙头拧紧,当他离开5小时后才被人发现并把水龙头拧紧,你能算出这期间浪费了多少毫升水吗?(结果用科学记数法表示)
解:5×3600×2×0.05=1800=1.8×103(毫升)
答:这期间浪费了1.8×103毫升水.
6.把2 230 000 000用科学记数法写成
2.23×10n-2的形式,求n 的值.
解:因为2 230 000 000
=2.23×109
所以n-2=9
所以n=11.
1.用科学记数法来表示大数
一般形式: a×10n( 1≤a<10,n为正整数)
2.用科学记数法表示大数的好处
3.用科学记数法a×10n表示大数关键要注意
两点:
(1)1≤a<10;
(2)当大数是大于10的整数时,n为整数位数减去1.
课堂小结:
2.若一个数用科学记数法表示为2.4×1021,则
这个数的整数部分的位数是( ).
A. 20 B.21 C.22 D.23
1.78 900 000用科学记数法表示为 ( ).
A. 789×105 B.0.789×109
C.7.89×107 D.7.89×108
巩固提高
C
C
3. 5.17×10n+1为用科学记数法表示的数,则
这个数的整数部分的位数是( ).
A. n-1 B.n C.n+1 D.n+2
D
4.若9 420 000用科学记数法表示为9.42×10n,
则n= .
6
5.若31 400 000用科学记数法表示a×10n,则
a= .
3.14
6.将0.05 ×105用科学记数法表示,则
0.05= .
5 ×103
7.已知一天有8.64 ×104秒若一年按365天计算,
则一年有 秒.(用科学记数法表示)
3.1536 ×107
8.64×104×365
=3153.6 ×104
=31 536 000
=3.1536 ×107
今天作业
课本第47页习题1.5第4、5题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
