苏科版九年级下册第6章 图形的相似(第一课时)课件((共19张PPT))
文档属性
| 名称 | 苏科版九年级下册第6章 图形的相似(第一课时)课件((共19张PPT)) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-10 07:25:27 | ||
图片预览






文档简介
(共19张PPT)
九年级(下册)
初中数学
苏州线上教育中心
专题复习:图形相似(1)
知识梳理
一、平行线分线段成比例
基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
(1)定义:在四条线段中,如果两条线段的比等于另两条线段的比,那么这四条线段叫做 .
成比例线段
(2)基本性质:如果a:b=c:d,那么 ;反之也成立.
ad=bc
特例:如果a:b=b:c,那么我们把b叫作a和c的 .
比例中项
二、比例线段
基础练习
1.已知a,b,c满足 ,且满足 .
(1)求a,b,c的值;
(2)若线段x是线段6a,b的比例中项,求x的值。
设一份为k或者设比值为k的方法实质是统一的,都是把未知数看做是以k为基本单位的数,从而都能够用k来表示,达到“消元”的效果。
基础练习
F
A
B
C
D
E
O
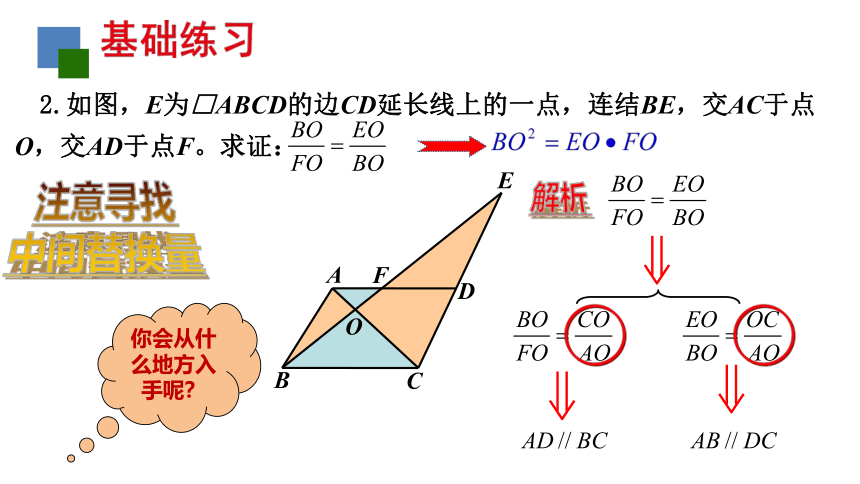
你会从什么地方入手呢?
2.如图,E为□ABCD的边CD延长线上的一点,连结BE,交AC于点
O,交AD于点F。求证:
解析
注意寻找
中间替换量
知识梳理
(3)黄金分割
如图,点B把线段AC分成两部分(AB>BC),如果 ,
那么称线段AC被点B ,点B为线段AC的 .
BC与AB(或AB与AC)的比称为黄金比,这个比值为 ,
约为 。
黄金分割
黄金分割点
0.618
二、比例线段
3.如图,下列条件不能判定△ADB∽△ABC的是( )
A.∠ABD=∠ACB B. ∠ADB=∠ABC
C. D.
基础练习
D
知识梳理
三、相似三角形及其判定与性质
1.定义:
(1)相似图形 : 的图形是相似形。
(2)相似三角形:各角对应 、各边对应 的两个三角形叫作相似三角形。
形状相同
相等
成比例
知识梳理
2.相似三角形的判定:
(1)按定义判定
(2) 的两个三角形相似。
(3) 的两个三角形相似。
(4) 的两个三角形相似。
两角分别相等
平行
三边成比例
两边成比例且夹角相等
(5) 于三角形一边的直线与其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
基础训练
DE:AC=1:5
BE:BC=1:5
BE:EC
1:4
比较:(1)相似三角形的面积之比等于相似比的平方;
(2)高相等,三角形面积之比等于底之比;
底相等,三角形面积之比等于高之比。
4.
知识梳理
四、相似多边形
1.定义:如果两个边数相同的多边形的各角 、各边 ,那么这两个多边形相似。相似多边形的对应边的比叫作 。
成比例
相等
相似比
2.性质:
(1)对应角 相等 、对应边 成比例 .
(1)相似多边形周长的比等于 相似比 .
(2)相似多边形面积的比等于 相似比的平方 .
知识梳理
五、图形的位似
1.定义:如果两个图形不仅相似,而且对应顶点的连线 ,对应边 ,像这样的两个图形叫做
位似图形, 这个交点叫做 ,位似图形的相似比又称为 .
相交于一点
互相平行或在同一直线上
位似中心
位似比
2.位似图形的性质:
(1)对应点所在直线都经过同一点
(2)对应边互相平行(或者在同一直线上);
(3)对应点到位似中心的距离之比等于相似比.
基础训练
5.如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的 1/4 ,那么点B′的坐标是( )
A.(3,2)
B.(-2,-3)
C.(2,3)或(-2,-3)
D.(3,2)或(-3,-2 )
D
B′
A′
C′
C′
B′
A′
注意:作一个图形的位似图形时,
(1)看清楚位似比,是将原图形放大还是缩小
(2)两个图形可以在位似中心的同侧,也可以在位似中心的异侧
典型例题
例1.如图,在△ABC中,点D是AC上的一点,点F为CB上的一点,且AD=BF,DF交AB于点E.
求证:
A
E
B
C
D
F
A
E
B
C
D
F
G
A
E
B
C
D
F
H
作平行构造
线段对应成比例
典型例题
例2.如图,在□ABCD中,点E为DC的中点,AE交BD于点G,且GD=3.
(1)求BD的长;
(2)连结AC交BD于点O,求DG:GO的值。
C
D
A
B
G
E
O
C
D
A
B
O
F
E
拓展:如图,在□ABCD中,点E为DC的任意一点。
(1)图中中哪几对相似三角形?请分别写出来;
(2)若 ,求BF的长及 的值。
例3:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°求证:AD BC=AP BP.
探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
典型例题
△DAP∽△PBC
∠ADP=∠BPC
“K字形”相似
“一线三等角”模型
∠ADP +∠APD = 180°- θ
∠BPC +∠APD = 180°- θ
∠ADP+∠APD= 90°
∠BPC+∠APD= 90°
也可利用外角性质∠DP B = ∠A+∠ADP
而∠DP B=∠DPC+∠BPC
【课堂收获】
你对本节课学习又有了哪些新的认识?
课堂小结
相似形
性质
判定
对应边成比例
对应角相等
对应线段之比等于相似比
比例线段
平行线分线段成比例
比例的基本性质
黄金分割
相似三角形
相似多边形
位似图形
相似应用
周长之比等于相似比
面积之比等于相似比的平方
性质
判定
对应边成比例
对应角相等
对应边成比例
对应角相等
位似作图
位似计算
联系特殊三角形
联系特殊四角形
联系动点问题
联系三角函数
联系一次函数
联系二次函数
两角对应相等
两边对应成比例,且夹角角相等
定义判定
三边对应成比例
平行相似
巩固练习
如图,在矩形ABCD中,E为BC上任意一点,DF⊥AE于点E。
(1)求证:△ABE与△DFA相似吗?请说明理由。
(2)若AB=6,AD=12,AE=10,求DF的长。
E
A
B
C
D
F
拓展:在□ABCD中,过点A作AE⊥BC,垂足为E,连结DE,F为线段DE上一点,且∠AFE= ∠B.
(1)求证:AD.EC=DF.DE;
(2)若AB=4,AD= ,AE=3,求AF的长。
C
A
B
D
E
F
谢
谢
大
家
九年级(下册)
初中数学
苏州线上教育中心
专题复习:图形相似(1)
知识梳理
一、平行线分线段成比例
基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
(1)定义:在四条线段中,如果两条线段的比等于另两条线段的比,那么这四条线段叫做 .
成比例线段
(2)基本性质:如果a:b=c:d,那么 ;反之也成立.
ad=bc
特例:如果a:b=b:c,那么我们把b叫作a和c的 .
比例中项
二、比例线段
基础练习
1.已知a,b,c满足 ,且满足 .
(1)求a,b,c的值;
(2)若线段x是线段6a,b的比例中项,求x的值。
设一份为k或者设比值为k的方法实质是统一的,都是把未知数看做是以k为基本单位的数,从而都能够用k来表示,达到“消元”的效果。
基础练习
F
A
B
C
D
E
O
你会从什么地方入手呢?
2.如图,E为□ABCD的边CD延长线上的一点,连结BE,交AC于点
O,交AD于点F。求证:
解析
注意寻找
中间替换量
知识梳理
(3)黄金分割
如图,点B把线段AC分成两部分(AB>BC),如果 ,
那么称线段AC被点B ,点B为线段AC的 .
BC与AB(或AB与AC)的比称为黄金比,这个比值为 ,
约为 。
黄金分割
黄金分割点
0.618
二、比例线段
3.如图,下列条件不能判定△ADB∽△ABC的是( )
A.∠ABD=∠ACB B. ∠ADB=∠ABC
C. D.
基础练习
D
知识梳理
三、相似三角形及其判定与性质
1.定义:
(1)相似图形 : 的图形是相似形。
(2)相似三角形:各角对应 、各边对应 的两个三角形叫作相似三角形。
形状相同
相等
成比例
知识梳理
2.相似三角形的判定:
(1)按定义判定
(2) 的两个三角形相似。
(3) 的两个三角形相似。
(4) 的两个三角形相似。
两角分别相等
平行
三边成比例
两边成比例且夹角相等
(5) 于三角形一边的直线与其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
基础训练
DE:AC=1:5
BE:BC=1:5
BE:EC
1:4
比较:(1)相似三角形的面积之比等于相似比的平方;
(2)高相等,三角形面积之比等于底之比;
底相等,三角形面积之比等于高之比。
4.
知识梳理
四、相似多边形
1.定义:如果两个边数相同的多边形的各角 、各边 ,那么这两个多边形相似。相似多边形的对应边的比叫作 。
成比例
相等
相似比
2.性质:
(1)对应角 相等 、对应边 成比例 .
(1)相似多边形周长的比等于 相似比 .
(2)相似多边形面积的比等于 相似比的平方 .
知识梳理
五、图形的位似
1.定义:如果两个图形不仅相似,而且对应顶点的连线 ,对应边 ,像这样的两个图形叫做
位似图形, 这个交点叫做 ,位似图形的相似比又称为 .
相交于一点
互相平行或在同一直线上
位似中心
位似比
2.位似图形的性质:
(1)对应点所在直线都经过同一点
(2)对应边互相平行(或者在同一直线上);
(3)对应点到位似中心的距离之比等于相似比.
基础训练
5.如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的 1/4 ,那么点B′的坐标是( )
A.(3,2)
B.(-2,-3)
C.(2,3)或(-2,-3)
D.(3,2)或(-3,-2 )
D
B′
A′
C′
C′
B′
A′
注意:作一个图形的位似图形时,
(1)看清楚位似比,是将原图形放大还是缩小
(2)两个图形可以在位似中心的同侧,也可以在位似中心的异侧
典型例题
例1.如图,在△ABC中,点D是AC上的一点,点F为CB上的一点,且AD=BF,DF交AB于点E.
求证:
A
E
B
C
D
F
A
E
B
C
D
F
G
A
E
B
C
D
F
H
作平行构造
线段对应成比例
典型例题
例2.如图,在□ABCD中,点E为DC的中点,AE交BD于点G,且GD=3.
(1)求BD的长;
(2)连结AC交BD于点O,求DG:GO的值。
C
D
A
B
G
E
O
C
D
A
B
O
F
E
拓展:如图,在□ABCD中,点E为DC的任意一点。
(1)图中中哪几对相似三角形?请分别写出来;
(2)若 ,求BF的长及 的值。
例3:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°求证:AD BC=AP BP.
探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
典型例题
△DAP∽△PBC
∠ADP=∠BPC
“K字形”相似
“一线三等角”模型
∠ADP +∠APD = 180°- θ
∠BPC +∠APD = 180°- θ
∠ADP+∠APD= 90°
∠BPC+∠APD= 90°
也可利用外角性质∠DP B = ∠A+∠ADP
而∠DP B=∠DPC+∠BPC
【课堂收获】
你对本节课学习又有了哪些新的认识?
课堂小结
相似形
性质
判定
对应边成比例
对应角相等
对应线段之比等于相似比
比例线段
平行线分线段成比例
比例的基本性质
黄金分割
相似三角形
相似多边形
位似图形
相似应用
周长之比等于相似比
面积之比等于相似比的平方
性质
判定
对应边成比例
对应角相等
对应边成比例
对应角相等
位似作图
位似计算
联系特殊三角形
联系特殊四角形
联系动点问题
联系三角函数
联系一次函数
联系二次函数
两角对应相等
两边对应成比例,且夹角角相等
定义判定
三边对应成比例
平行相似
巩固练习
如图,在矩形ABCD中,E为BC上任意一点,DF⊥AE于点E。
(1)求证:△ABE与△DFA相似吗?请说明理由。
(2)若AB=6,AD=12,AE=10,求DF的长。
E
A
B
C
D
F
拓展:在□ABCD中,过点A作AE⊥BC,垂足为E,连结DE,F为线段DE上一点,且∠AFE= ∠B.
(1)求证:AD.EC=DF.DE;
(2)若AB=4,AD= ,AE=3,求AF的长。
C
A
B
D
E
F
谢
谢
大
家
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
