苏科版八年级下册第9章 中心对称图形——平行四边形课件((共12张PPT))
文档属性
| 名称 | 苏科版八年级下册第9章 中心对称图形——平行四边形课件((共12张PPT)) |  | |
| 格式 | pptx | ||
| 文件大小 | 17.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-10 07:28:22 | ||
图片预览





文档简介
(共12张PPT)
四边形 (1)
复习引入
将△ABC绕着一边中点O旋转180°:
平行四边形ABCD
△ABC的一条中位线OE
第
9
章
图形的旋转、中心对称与中心对称图形的性质
平行四边形、矩形、菱形、正方形的性质定理和判定定理
三角形的中位线
分类复习
1.如图1,正方形的四个顶点都在圆上,正方形的两条对角线将圆分成相同的四部分,分别以正方形的四条边为直径向外作半圆,组成如图所示的图案.这个图案绕对角线的交点至少旋转_____°能与原来图案重合.
类型一 旋转、中心对称与中心对称图形
变式:
如图2,点O是正五边形ABCDE的中心,分别以各边为直径向正五边形的外部作半圆,组成一幅美丽的图案.这个图案绕点O至少旋转___°能与原来图案重合.
图1
90
72
图2
分类复习
2.如图,边长为2的正方形ABCD中对角线BD上有一点P,连接AP,作PE⊥BC于点E, PF⊥CD于点F, 连接EF.则下列结论中正确的是________.
①AP=EF;
②∠PAD=∠PEF;
③AP⊥EF;
④EF的最小值为1;
⑤△APD的面积与四边形PEFD的面积相等.
类型二 平行四边形、矩形、菱形、正方形的性质与判定
①②③⑤
分类复习
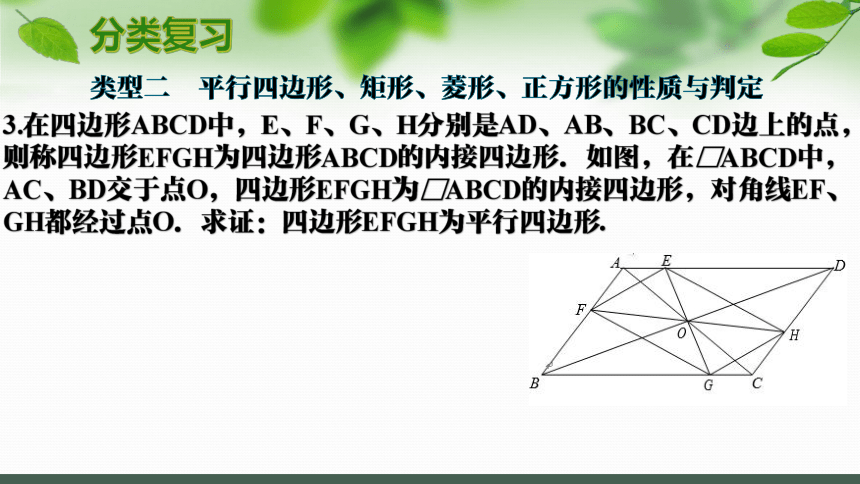
3.在四边形ABCD中,E、F、G、H分别是AD、AB、BC、CD边上的点,则称四边形EFGH为四边形ABCD的内接四边形.如图,在□ABCD中,AC、BD交于点O,四边形EFGH为□ABCD的内接四边形,对角线EF、GH都经过点O.求证:四边形EFGH为平行四边形.
类型二 平行四边形、矩形、菱形、正方形的性质与判定
分类复习
变式:
顶点在矩形边上的菱形叫做矩形的内接菱形.如图,矩形ABCD中AB=a, BC=b(a<b).(1)、(2)、(3)是三种不同内接菱形的方式.
(1)试比较图①、②、③中内接菱形的面积大小关系;
(2)你还能画出矩形的第四种内接菱形吗?若能,在图④中画出;若不能请说明理由.
类型二 平行四边形、矩形、菱形、正方形的性质与判定
分类复习
类型二 平行四边形、矩形、菱形、正方形的性质与判定
分类复习
类型二 平行四边形、矩形、菱形、正方形的性质与判定
分类复习
4.如图,□ABCD的对角线AC、BD相交于点O,E、F分别是AO、BO的中点.若AC+BD=22cm,△AOB的周长是17cm,则EF=_____cm.
类型三 三角形的中位线
3
分类复习
5.如图,□ABCD的对角线AC、BD相交于点O,E是DC延长线上一点.
且CD=CE,连接AE交BC于点F,交BD于点G.求证:AB=2OF.
类型三 三角形的中位线
课堂小结
旋转中心、
旋转方向、
旋转角度
两边中点
第三边
第三边的一半
课堂小结
平行四边形
菱形
有一组邻边相等
有一个角是直角
有一个角是直角
有一组邻边相等
有一组邻边相等、有一个角是直角
四边形 (1)
复习引入
将△ABC绕着一边中点O旋转180°:
平行四边形ABCD
△ABC的一条中位线OE
第
9
章
图形的旋转、中心对称与中心对称图形的性质
平行四边形、矩形、菱形、正方形的性质定理和判定定理
三角形的中位线
分类复习
1.如图1,正方形的四个顶点都在圆上,正方形的两条对角线将圆分成相同的四部分,分别以正方形的四条边为直径向外作半圆,组成如图所示的图案.这个图案绕对角线的交点至少旋转_____°能与原来图案重合.
类型一 旋转、中心对称与中心对称图形
变式:
如图2,点O是正五边形ABCDE的中心,分别以各边为直径向正五边形的外部作半圆,组成一幅美丽的图案.这个图案绕点O至少旋转___°能与原来图案重合.
图1
90
72
图2
分类复习
2.如图,边长为2的正方形ABCD中对角线BD上有一点P,连接AP,作PE⊥BC于点E, PF⊥CD于点F, 连接EF.则下列结论中正确的是________.
①AP=EF;
②∠PAD=∠PEF;
③AP⊥EF;
④EF的最小值为1;
⑤△APD的面积与四边形PEFD的面积相等.
类型二 平行四边形、矩形、菱形、正方形的性质与判定
①②③⑤
分类复习
3.在四边形ABCD中,E、F、G、H分别是AD、AB、BC、CD边上的点,则称四边形EFGH为四边形ABCD的内接四边形.如图,在□ABCD中,AC、BD交于点O,四边形EFGH为□ABCD的内接四边形,对角线EF、GH都经过点O.求证:四边形EFGH为平行四边形.
类型二 平行四边形、矩形、菱形、正方形的性质与判定
分类复习
变式:
顶点在矩形边上的菱形叫做矩形的内接菱形.如图,矩形ABCD中AB=a, BC=b(a<b).(1)、(2)、(3)是三种不同内接菱形的方式.
(1)试比较图①、②、③中内接菱形的面积大小关系;
(2)你还能画出矩形的第四种内接菱形吗?若能,在图④中画出;若不能请说明理由.
类型二 平行四边形、矩形、菱形、正方形的性质与判定
分类复习
类型二 平行四边形、矩形、菱形、正方形的性质与判定
分类复习
类型二 平行四边形、矩形、菱形、正方形的性质与判定
分类复习
4.如图,□ABCD的对角线AC、BD相交于点O,E、F分别是AO、BO的中点.若AC+BD=22cm,△AOB的周长是17cm,则EF=_____cm.
类型三 三角形的中位线
3
分类复习
5.如图,□ABCD的对角线AC、BD相交于点O,E是DC延长线上一点.
且CD=CE,连接AE交BC于点F,交BD于点G.求证:AB=2OF.
类型三 三角形的中位线
课堂小结
旋转中心、
旋转方向、
旋转角度
两边中点
第三边
第三边的一半
课堂小结
平行四边形
菱形
有一组邻边相等
有一个角是直角
有一个角是直角
有一组邻边相等
有一组邻边相等、有一个角是直角
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
