华东师大版七上数学 3.1.3列代数式 课件(共16张PPT)
文档属性
| 名称 | 华东师大版七上数学 3.1.3列代数式 课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-10 09:13:59 | ||
图片预览






文档简介
(共16张PPT)
列代数式
3.1 列代数式
下列各式是否是代数式?如果是,判断其书写
是否正确。
(1)0 ;(2)ab=ba ;(3)s÷v;(4)b× ;
(5)x+2>3;(6)5m-2m;(7)
某地区夏季高山上的温度从山脚处开始每升高100米降低0.7℃。如果山脚温度是28 ℃,那么山上300米处的温度为 ;一般地,山上x米处的温度为 。
25.9℃
(28-0.007x)℃
那么山上2000米处的温度是 。
14℃
在解决实际问题时,列出代数式可以使问题变得简洁。
列代数式的意义
精讲:把问题中与数量有关的词语,用含有数、字母及运算符号表示出来,就是列代数式。
列代数式的步骤:
(1)抓住关键词,理解其意义。如:大,小,多,少,和,差,积,商,倍等。
(2)明确运算顺序。
(3)概括原题,正确使用括号。
什么是列代数式?列代数式的步骤是什么?
设某数为 ,用代数式表示:
(1)比该数的 3倍大1的数;
(2)该数与它的 的和;
(3)该数与 的和的3倍;
(4)该数的倒数与5的差。
列文字语言的代数式
例3
(x≠0)
用代数式表示:
(1)a、b两数的平方和;
(2)a、b两数的和的平方;
(3)a、b两数的和与它们的差的乘积;
(4)偶数,奇数。
例4
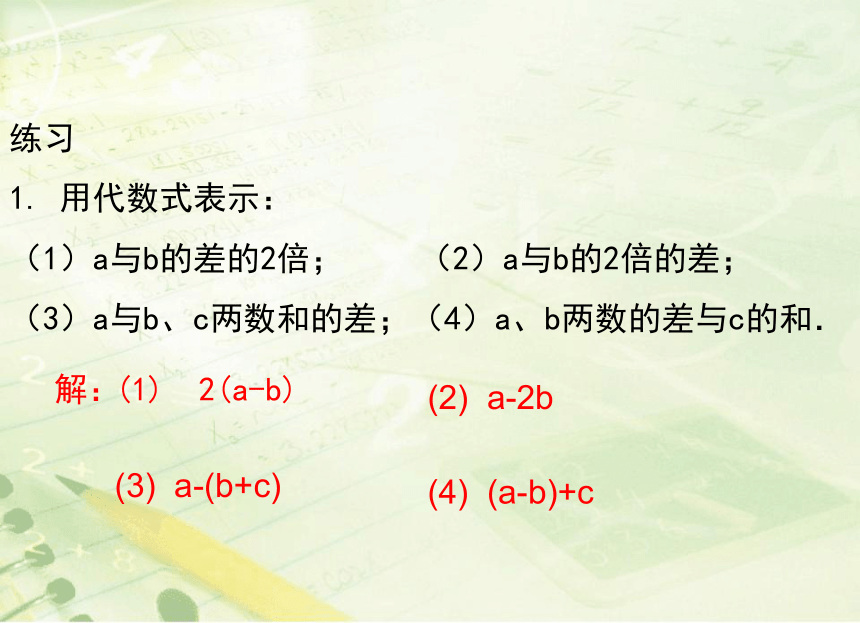
练习
1. 用代数式表示:
(1)a与b的差的2倍; (2)a与b的2倍的差;
(3)a与b、c两数和的差;(4)a、b两数的差与c的和.
(1) 2(a-b)
(2) a-2b
(3) a-(b+c)
(4) (a-b)+c
解:
2. 填空:
(1)三个连续整数,中间一个是n,则第一个和第三个整数分别是 、 ;
(2)三个连续偶数,中间一个是2n,则第一个和第三个偶数分别是 、 .
(3)三个连续奇数,中间一个是2n+1,则第一个和第三个奇数分别是 、 .
n-1
n+1
2n-2
2n+2
2n-1
2n+3
3、用语言叙述代数式 ,
正确的是( )
A、a, b两数的平方差
B、a与b差的平方
C、a与b平方的差
D、 b, a两数的平方差
C
4、判断:
甲数为x,判断下列各式是否正确 :
(1) 甲数的 倍与4的和:
(2) 比甲数小7%:
(3) 比甲数的一半的相反数大2:
(4) 甲数除2的商与5的差:
(5) 甲数的平方与3的平方的差:
( )
( )
( )
( )
( )
×
×
×
某市出租车收费标准是:起步价为7元,3千米后每千米为1.8元。
(1)某人乘坐出租车4千米需 元;6千米需 元;
(2)若这人乘坐x(x>3)千米,需 元。
8.8
12.4
7+1.8(x-3)=1.8x+1.6
(1.8x+1.6)
坐4千米需要:7+1.8×(4-3)=8.8元
坐6千米需要:7+1.8×(6-3)=12.4元
列实际问题中的代数式
2、如图所示,用代数式表示图中阴影部分的面积。
本节课我们学习了下面几个内容:
④列实际问题中的代数式。
①列代数式的意义;
③列文字语言的代数式;
②列代数式的步骤;
作业:
探索规律
图形编号 (1) (2) (3) (4) (5) (6)
棋子个数
(2)按这种方式,摆第n个正方形需要多少棋子?
(1)按图示规律填写下表:
某市为了加强公民的节水意识,制定了以下用水标准:每户每月用水未超过8立方米时,每立方米收费1.00元,并加收0.20元的城市污水处理费;超过8立方米的部分每立方米收费1.50元,并加收0.40元的城市污水处理费.某户某月用水量为x立方米,问这个月水费是多少元?
解:
当x>8时,水费为 8×1.00+1.50(x-8)+0.40
=(1.50x-3.60)(元).
当x≤8时,水费为1.00x+0.20=(x+0.20)(元);
试一试:
图中由长方形和正方形拼 成的大正方形的面积等于 _____。我们还可以 这样想,图中大正方形的 边长是____,因此它 的面积是______。
由此,我们可以得到一个
等式:____=____。
a +2ab+b
a+b
(a+b)
(a+b)
a +2ab+b
列代数式
3.1 列代数式
下列各式是否是代数式?如果是,判断其书写
是否正确。
(1)0 ;(2)ab=ba ;(3)s÷v;(4)b× ;
(5)x+2>3;(6)5m-2m;(7)
某地区夏季高山上的温度从山脚处开始每升高100米降低0.7℃。如果山脚温度是28 ℃,那么山上300米处的温度为 ;一般地,山上x米处的温度为 。
25.9℃
(28-0.007x)℃
那么山上2000米处的温度是 。
14℃
在解决实际问题时,列出代数式可以使问题变得简洁。
列代数式的意义
精讲:把问题中与数量有关的词语,用含有数、字母及运算符号表示出来,就是列代数式。
列代数式的步骤:
(1)抓住关键词,理解其意义。如:大,小,多,少,和,差,积,商,倍等。
(2)明确运算顺序。
(3)概括原题,正确使用括号。
什么是列代数式?列代数式的步骤是什么?
设某数为 ,用代数式表示:
(1)比该数的 3倍大1的数;
(2)该数与它的 的和;
(3)该数与 的和的3倍;
(4)该数的倒数与5的差。
列文字语言的代数式
例3
(x≠0)
用代数式表示:
(1)a、b两数的平方和;
(2)a、b两数的和的平方;
(3)a、b两数的和与它们的差的乘积;
(4)偶数,奇数。
例4
练习
1. 用代数式表示:
(1)a与b的差的2倍; (2)a与b的2倍的差;
(3)a与b、c两数和的差;(4)a、b两数的差与c的和.
(1) 2(a-b)
(2) a-2b
(3) a-(b+c)
(4) (a-b)+c
解:
2. 填空:
(1)三个连续整数,中间一个是n,则第一个和第三个整数分别是 、 ;
(2)三个连续偶数,中间一个是2n,则第一个和第三个偶数分别是 、 .
(3)三个连续奇数,中间一个是2n+1,则第一个和第三个奇数分别是 、 .
n-1
n+1
2n-2
2n+2
2n-1
2n+3
3、用语言叙述代数式 ,
正确的是( )
A、a, b两数的平方差
B、a与b差的平方
C、a与b平方的差
D、 b, a两数的平方差
C
4、判断:
甲数为x,判断下列各式是否正确 :
(1) 甲数的 倍与4的和:
(2) 比甲数小7%:
(3) 比甲数的一半的相反数大2:
(4) 甲数除2的商与5的差:
(5) 甲数的平方与3的平方的差:
( )
( )
( )
( )
( )
×
×
×
某市出租车收费标准是:起步价为7元,3千米后每千米为1.8元。
(1)某人乘坐出租车4千米需 元;6千米需 元;
(2)若这人乘坐x(x>3)千米,需 元。
8.8
12.4
7+1.8(x-3)=1.8x+1.6
(1.8x+1.6)
坐4千米需要:7+1.8×(4-3)=8.8元
坐6千米需要:7+1.8×(6-3)=12.4元
列实际问题中的代数式
2、如图所示,用代数式表示图中阴影部分的面积。
本节课我们学习了下面几个内容:
④列实际问题中的代数式。
①列代数式的意义;
③列文字语言的代数式;
②列代数式的步骤;
作业:
探索规律
图形编号 (1) (2) (3) (4) (5) (6)
棋子个数
(2)按这种方式,摆第n个正方形需要多少棋子?
(1)按图示规律填写下表:
某市为了加强公民的节水意识,制定了以下用水标准:每户每月用水未超过8立方米时,每立方米收费1.00元,并加收0.20元的城市污水处理费;超过8立方米的部分每立方米收费1.50元,并加收0.40元的城市污水处理费.某户某月用水量为x立方米,问这个月水费是多少元?
解:
当x>8时,水费为 8×1.00+1.50(x-8)+0.40
=(1.50x-3.60)(元).
当x≤8时,水费为1.00x+0.20=(x+0.20)(元);
试一试:
图中由长方形和正方形拼 成的大正方形的面积等于 _____。我们还可以 这样想,图中大正方形的 边长是____,因此它 的面积是______。
由此,我们可以得到一个
等式:____=____。
a +2ab+b
a+b
(a+b)
(a+b)
a +2ab+b
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
