【新课标】2.4估算 课件(共22张PPT)
文档属性
| 名称 | 【新课标】2.4估算 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 14:16:38 | ||
图片预览








文档简介
(共22张PPT)
2.4估算
北师大版 八年级上册
教学目标
1、掌握估算的基本方法,学会用估算的方法去判断值的大概范围;
2、可以运用估算的方法解决实际问题;
情景导入
某地开辟了一块长方形的荒地,新建一个环保主题公园.已知这块荒地的长是宽的2倍,它的面积为400 000 m2.
(1)公园的宽大约是多少?它有1 000m吗?
(2)如果要求结果精确到10m,它的宽大约是多少?与同伴进行交流.
(3)该公园中心有一个圆形花圃,它的面积是 800m2,你能估计它的半径吗?(结果精确到1m)
新知讲解
1000
2000
S=400000
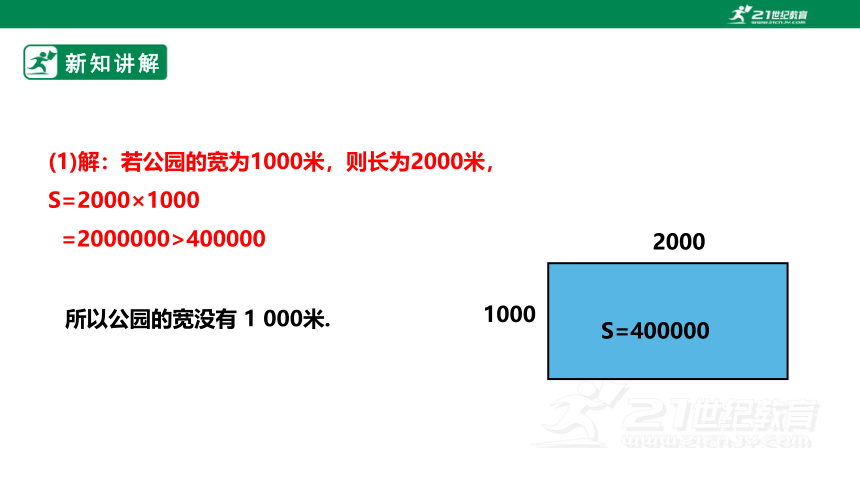
(1)解:若公园的宽为1000米,则长为2000米,S=2000×1000
=2000000>400000
所以公园的宽没有 1 000米.
(2)解:设公园的宽为x米,则长为2x米,得:
2x·x=400000
x=
新知讲解
x
2x
S=400000
x≈450
新知讲解
S=800
r
(3)解:设花园的半径为r 米,得
πr2=800
r2≈254.8
r=
r≈16
怎么估算无理数的大小?
议一议
(1)下列计算结果正确吗?你是怎样判断的?与同伴进行交流.
;
解:因为()2=0.43, 0.0662=0.004356,所以0.066不正确.
因为()3=900,963=884736,所以96不正确.
因为()2=2536,60.42=3648.16,所以60.4不正确.
新知讲解
(2)你能估算的大小吗?(结果精确到1)
注意:精确到1m是四舍五入到个位
解:因为729<900<1000,
所以<<,
即 9< <10,
得: 10
总结归纳
估算的一般步骤:
(1)估计整数部分是几位数;
(2)确定最高位上的数字;
(3)确定下一位上的数字;
(4)依此类推,直到确定出个位上的数字,或者按要求精确到小数点后的某一位.
典例精析
例 生活经验表明,靠墙摆放梯子时,若梯子底端离墙的距离约为梯子长度的,则梯子比较稳定.现有一长度为6 m的梯子,当梯子稳定摆放时,它的顶端能达到5.6m高的墙头吗
典例精析
解:设梯子稳定摆放时的高度为xm,
此时梯子底端离墙的距离恰为梯子长度的,
根据勾股定理,有x2+(6)2=62,即x2=32,x=
因为5.62=31.36<32,所以>5.6.
因此,梯子稳定摆放时,它的顶端能够达到5.6m高的墙头.
议一议
(1)通过估算,你能比较与的大小吗?你是怎样想的?与同伴进行交流.
(2)小明是这样想的: 与 的分母相同,只要比较它们的分子就可以了.因为, 因此
你认为小明的想法正确吗?
正确
总结归纳
1.用估算法比较两个数的大小(其中至少有一个是无理数)时,一般先用分析的方法估算出无理数的大致范围,再比较.
2.比较大小的两个数中如果有含根号的数,常常有如下比较方法:
(1)先找个中间值,再比较;
(2)先把两数平方或立方,再比较.
课堂练习
1.下列选项中的整数,与最接近的是( )
A.3 B.4 C.5 D.6
2.估计+1的值在( )
A.2和3之间 B.3和4之间
C.4和5之间 D.5和6之间
B
C
课堂练习
3.正三角形的边长为6cm,高为h,则h= ,若精确到个位,那么h约为 cm.
4.比较大小: ;
______ 0.62.
5.2
>
<
课堂练习
5.已知的整数部分为a,小数部分为b,求代数式a2-a-b的值.
解:∵9<13<16,∴3<
∴a=3,b=
∴
=9-3-()
=6-
=9-
课堂练习
6.已知5 +的小数部分是a,5-的小数部分b,
求(1)a+b的值;(2)a-b的值
解:(1)因为3,所以8<5+,1<5-
所以a=5+
b=5-
所以a+b=()+(4-)=1
(2)a-b=
课堂总结
估算
估算无理数大小的方法
利用估算比较两个数的大小
夹逼的思想
估算的实际应用
板书设计
2.4估算
估算无理数大小的方法:
(1)利用乘方与开方互为逆运算来确定无理数的整数部分;
(2)根据所要求的误差确定小数部分.
作业布置
教材34页习题第1、2、6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.4估算
北师大版 八年级上册
教学目标
1、掌握估算的基本方法,学会用估算的方法去判断值的大概范围;
2、可以运用估算的方法解决实际问题;
情景导入
某地开辟了一块长方形的荒地,新建一个环保主题公园.已知这块荒地的长是宽的2倍,它的面积为400 000 m2.
(1)公园的宽大约是多少?它有1 000m吗?
(2)如果要求结果精确到10m,它的宽大约是多少?与同伴进行交流.
(3)该公园中心有一个圆形花圃,它的面积是 800m2,你能估计它的半径吗?(结果精确到1m)
新知讲解
1000
2000
S=400000
(1)解:若公园的宽为1000米,则长为2000米,S=2000×1000
=2000000>400000
所以公园的宽没有 1 000米.
(2)解:设公园的宽为x米,则长为2x米,得:
2x·x=400000
x=
新知讲解
x
2x
S=400000
x≈450
新知讲解
S=800
r
(3)解:设花园的半径为r 米,得
πr2=800
r2≈254.8
r=
r≈16
怎么估算无理数的大小?
议一议
(1)下列计算结果正确吗?你是怎样判断的?与同伴进行交流.
;
解:因为()2=0.43, 0.0662=0.004356,所以0.066不正确.
因为()3=900,963=884736,所以96不正确.
因为()2=2536,60.42=3648.16,所以60.4不正确.
新知讲解
(2)你能估算的大小吗?(结果精确到1)
注意:精确到1m是四舍五入到个位
解:因为729<900<1000,
所以<<,
即 9< <10,
得: 10
总结归纳
估算的一般步骤:
(1)估计整数部分是几位数;
(2)确定最高位上的数字;
(3)确定下一位上的数字;
(4)依此类推,直到确定出个位上的数字,或者按要求精确到小数点后的某一位.
典例精析
例 生活经验表明,靠墙摆放梯子时,若梯子底端离墙的距离约为梯子长度的,则梯子比较稳定.现有一长度为6 m的梯子,当梯子稳定摆放时,它的顶端能达到5.6m高的墙头吗
典例精析
解:设梯子稳定摆放时的高度为xm,
此时梯子底端离墙的距离恰为梯子长度的,
根据勾股定理,有x2+(6)2=62,即x2=32,x=
因为5.62=31.36<32,所以>5.6.
因此,梯子稳定摆放时,它的顶端能够达到5.6m高的墙头.
议一议
(1)通过估算,你能比较与的大小吗?你是怎样想的?与同伴进行交流.
(2)小明是这样想的: 与 的分母相同,只要比较它们的分子就可以了.因为, 因此
你认为小明的想法正确吗?
正确
总结归纳
1.用估算法比较两个数的大小(其中至少有一个是无理数)时,一般先用分析的方法估算出无理数的大致范围,再比较.
2.比较大小的两个数中如果有含根号的数,常常有如下比较方法:
(1)先找个中间值,再比较;
(2)先把两数平方或立方,再比较.
课堂练习
1.下列选项中的整数,与最接近的是( )
A.3 B.4 C.5 D.6
2.估计+1的值在( )
A.2和3之间 B.3和4之间
C.4和5之间 D.5和6之间
B
C
课堂练习
3.正三角形的边长为6cm,高为h,则h= ,若精确到个位,那么h约为 cm.
4.比较大小: ;
______ 0.62.
5.2
>
<
课堂练习
5.已知的整数部分为a,小数部分为b,求代数式a2-a-b的值.
解:∵9<13<16,∴3<
∴a=3,b=
∴
=9-3-()
=6-
=9-
课堂练习
6.已知5 +的小数部分是a,5-的小数部分b,
求(1)a+b的值;(2)a-b的值
解:(1)因为3,所以8<5+,1<5-
所以a=5+
b=5-
所以a+b=()+(4-)=1
(2)a-b=
课堂总结
估算
估算无理数大小的方法
利用估算比较两个数的大小
夹逼的思想
估算的实际应用
板书设计
2.4估算
估算无理数大小的方法:
(1)利用乘方与开方互为逆运算来确定无理数的整数部分;
(2)根据所要求的误差确定小数部分.
作业布置
教材34页习题第1、2、6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
