12.2三角形全等的判定(HL) 课件(共25张PPT)
文档属性
| 名称 | 12.2三角形全等的判定(HL) 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-09 13:09:14 | ||
图片预览







文档简介
(共25张PPT)
12.2三角形全等的判定(HL)
人教版八年级上册
知识回顾
1.什么叫全等三角形?
能够完全重合的两个三角形叫做全等三角形
2.证明三角形全等的判定方法有哪些?
①三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”).
②两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”)
③两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或者“ASA”)
④两角和其中一个角的对边分别相等的两个三角形全等(可以简写成“角角边”或者“AAS”)
教学目标
2. 能运用三角形全等的判定方法判断两个直角三角形全等.
1. 探究直角三角形全等的判定方法.
新知导入
经过前面的学习,我们知道了4种证明三角形全等的方法,对于特殊而又常用的直角三角形,有没有专属于它的特殊方法呢?这节课我们就来一起探究一下吧
你知道哪些关于直角三角形的性质?
1、有一个内角等于90°,是直角
2、两个锐角互余
3、直角所对的边最长,叫斜边
4、组成直角的两边叫直角边
A
B
C
┐
新知探究
问题1:如何探究直角三角形专属的全等的判定方法呢?
类比最开始判定三角形全等的时候,我们是从 条件开始探究的,所以直角三角形全等,我们可以尝试从这个角度进行探究。
边
那就从我们身边的直角三角板开始吧
新知探究
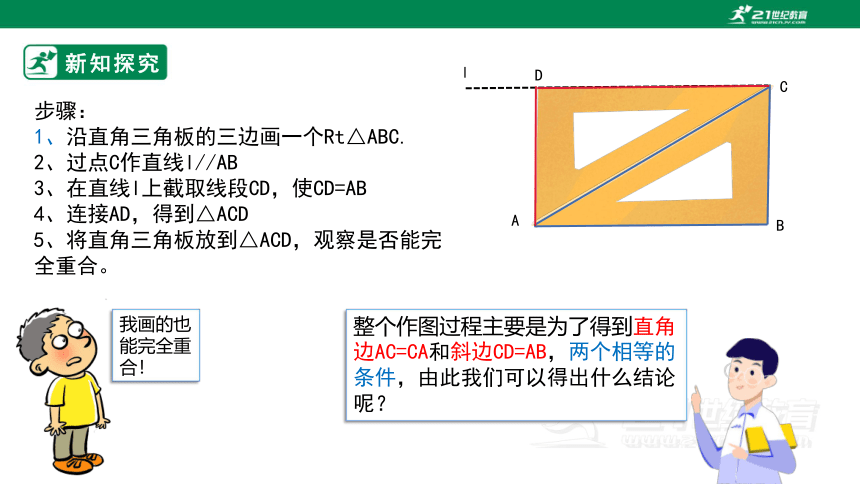
步骤:
1、沿直角三角板的三边画一个Rt△ABC.
2、过点C作直线l//AB
3、在直线l上截取线段CD,使CD=AB
4、连接AD,得到△ACD
5、将直角三角板放到△ACD,观察是否能完全重合。
A
B
C
l
D
我画的也能完全重合!
整个作图过程主要是为了得到直角边AC=CA和斜边CD=AB,两个相等的条件,由此我们可以得出什么结论呢?
新知归纳
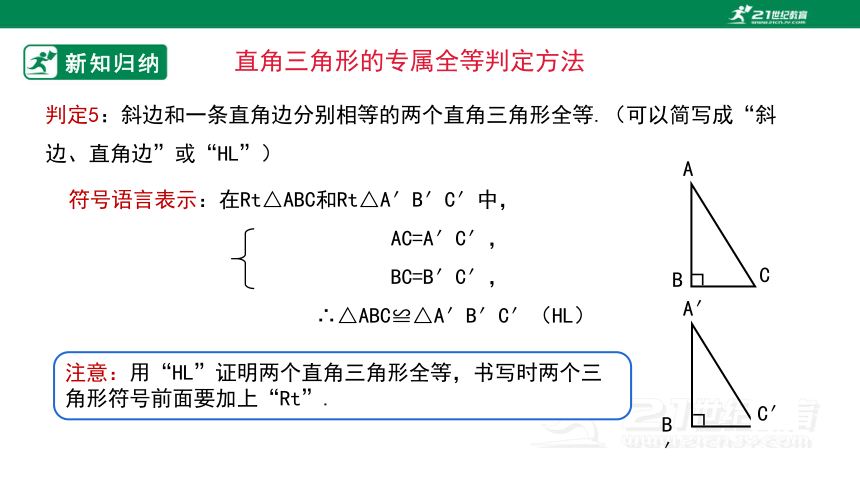
判定5:斜边和一条直角边分别相等的两个直角三角形全等.(可以简写成“斜边、直角边”或“HL”)
符号语言表示:在Rt△ABC和Rt△A′B′C′中,
AC=A′C′,
BC=B′C′,
∴△ABC≌△A′B′C′(HL).
注意:用“HL”证明两个直角三角形全等,书写时两个三角形符号前面要加上“Rt”.
C′
直角三角形的专属全等判定方法
新知归纳
已知条件 可选择的判定方法 需寻找的条件
一锐角对应相等
斜边对应相等
一直角边对应相等
直角三角形全等方法大归纳
ASA或AAS
可证直角与已知锐角的夹边对应相等或者与锐角(或直角)的对边对应相等
HL或AAS
可证一直角边对应相等或证一锐角对应相等
HL或ASA或AAS
可证斜边对应相等或证已知边相邻的锐角对应相等或证已知边所对的锐角对应相等
C′
新知练习
判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由:
(1)一个锐角和这个角的对边对应相等; ( )
(2)一个锐角和这个角的邻边对应相等; ( )
(3)一个锐角和斜边对应相等; ( )
(4)两直角边对应相等; ( )
(5)一条直角边和斜边对应相等 ( )
HL
AAS或ASA
SAS
AAS
AAS
判一判
C′
新知典例
例1 如图,AC⊥BC,BD⊥AD,垂足分别为C,D,AC=BD.求证:BC=AD.
证明:∵AC⊥BC,BD⊥AD,
∴∠C与∠D都是直角.
在Rt△ABC和Rt△BAD中,
AB=BA,
AC=BD,
∴Rt△ABC≌Rt△BAD(HL).
∴BC=AD.
课堂练习
变式 如图,AC⊥BC,BD⊥AD,要证△ABC≌△BAD,需要添加一个什么条件?请说明理由.
(1) AD = BC 理由: HL
(2) AC = BD 理由: HL
(3) ∠DBA =∠CAB 理由: AAS
(4) ∠DAB =∠CBA 理由: AAS
新知典例
证明:∵CE=BF,
∴CE-FE=BF-EF,即CF=BE.
在Rt△ABE和Rt△DCF中,
AB=DC,
BE=CF,
∴Rt△ABE≌Rt△DCF(HL).
∴AE=DF.
例2 如图,AB=CD,AE⊥BC,DF⊥BC,垂足分别为E,F,CE=BF.求证:AE=DF.
A
B
C
E
D
F
课堂总结
三角形全等的判定
HL
对比
探究
应用
斜边和一条直角边分别相等的两个直角三角形全等
根据已知条件选择适合证明两个直角三角形全等的方法
利用“HL”解决实际问题
课堂练习
1.如图,BF=CE,AE⊥BC,DF⊥BC,添加一个条件____,即可证明Rt△ABE≌Rt△DCF.下列添加的条件不正确的是( )
A.AB=DC B.AE=BF
C.EA=FD D.∠A=∠D
B
课堂练习
2.下列说法不正确的是( )
A.两条直角边对应相等的两个直角三角形全等
B.一锐角和斜边对应相等的两个直角三角形全等
C.斜边和一直角边对应相等的两个直角三角形全等
D.有两边相等的两个直角三角形全等
D
课堂练习
3.已知:如图,AE⊥BC,DF⊥BC,垂足分别为E,F,AE=DF,AB=DC,则△ ≌△ (HL).
ABE
DCF
证明:∵在△ABE和△DCF中,
AE⊥BC,DF⊥BC,AE=DF,AB=DC,
符合直角三角形全等条件HL,
所以△ABE≌△DCF,
课堂练习
4.如图,正方形网格中,点A,B,C,D均在格点上,则∠ACD+∠BDC= °.
90
解:在Rt△AEC和Rt△DAB中
∴Rt△AEC≌Rt△DAB(HL)
∴∠ACE=∠ABD
∵∠EAC+∠ACE=90°
∴∠EAC+∠ABD=90°
∴∠AFB=90°,即∠CFD=90°
∴∠ACD+∠BDC=90°
课堂练习
5.如图,AB⊥BC、DC⊥BC,垂足分别为B、C,AB=6,BC=8,CD=2,点P为BC边上一动点,当BP= 时,形成的Rt△ABP与Rt△PCD全等.
2
解:当BP=2时,Rt△ABP≌Rt△PCD
∵BC=8,BP=2
∴PC=6
∵AB⊥BC、DC⊥BC
∴∠B=∠C=90°
在△ABP和△PCD中
∴△ABP≌△PCD(SAS)
课堂练习
6.如图,在△ABC中,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,E,F为垂足,AE=CF.求证:∠ACB=90°.
证明:如图,在Rt△ACE和Rt△CBF中,
∴Rt△ACE≌Rt△CBF(HL)
∴∠EAC=∠BCF
∵∠EAC+∠ACE=90°
∴∠ACE+∠BCF=90°
∴∠ACB=180°﹣90°=90°
课堂练习
7.如图在△CDE中,∠DCE=90°,DC=CE,DA⊥AB于A,EB⊥AB于B,试判断AB与AD,BE之间的数量关系,并证明.
解:结论:AB=AD+BE.
证明:∵DA⊥AB于A,EB⊥AB于B
∴∠A=∠B;
∵∠DCE=90°,
∴∠ADC+∠ACD=90°,∠ACD+∠ECB=90°;
∴∠ADC=∠ECB;
又∵DC=CE,
在△ACD和△BEC中,
∴△ACD≌△BEC;
∴AD=BC,AC=BE;
∴AB=AC+CB=BE+AD.
课堂练习
8.如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=5cm,P,Q两点分别在AC上和过点A且垂直AC的射线AM上运动,且PQ=AB.当点P运动到AC上什么位置时,△ABC与△QPA全等?
A
B
C
P
M
Q
解:①当点P运动到AP=BC的位置时,
在Rt△APQ和Rt△CBA中,
PQ=BA,
AP=BC,
∴Rt△APQ≌Rt△CBA(HL).
∴AP=BC=5cm.
课堂练习
解:②当点P运动到AP=AC的位置时,
在Rt△APQ和Rt△CAB中,
PQ=AB,
AP=CA,
∴Rt△APQ≌Rt△CAB(HL).
∴AP=AC=10cm.
综上,当点P运动到使AP=5cm或AP=10cm位置时,
△APQ和△CAB全等.
A
B
C(P)
M
Q
作业布置
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
12.2三角形全等的判定(HL)
人教版八年级上册
知识回顾
1.什么叫全等三角形?
能够完全重合的两个三角形叫做全等三角形
2.证明三角形全等的判定方法有哪些?
①三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”).
②两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”)
③两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或者“ASA”)
④两角和其中一个角的对边分别相等的两个三角形全等(可以简写成“角角边”或者“AAS”)
教学目标
2. 能运用三角形全等的判定方法判断两个直角三角形全等.
1. 探究直角三角形全等的判定方法.
新知导入
经过前面的学习,我们知道了4种证明三角形全等的方法,对于特殊而又常用的直角三角形,有没有专属于它的特殊方法呢?这节课我们就来一起探究一下吧
你知道哪些关于直角三角形的性质?
1、有一个内角等于90°,是直角
2、两个锐角互余
3、直角所对的边最长,叫斜边
4、组成直角的两边叫直角边
A
B
C
┐
新知探究
问题1:如何探究直角三角形专属的全等的判定方法呢?
类比最开始判定三角形全等的时候,我们是从 条件开始探究的,所以直角三角形全等,我们可以尝试从这个角度进行探究。
边
那就从我们身边的直角三角板开始吧
新知探究
步骤:
1、沿直角三角板的三边画一个Rt△ABC.
2、过点C作直线l//AB
3、在直线l上截取线段CD,使CD=AB
4、连接AD,得到△ACD
5、将直角三角板放到△ACD,观察是否能完全重合。
A
B
C
l
D
我画的也能完全重合!
整个作图过程主要是为了得到直角边AC=CA和斜边CD=AB,两个相等的条件,由此我们可以得出什么结论呢?
新知归纳
判定5:斜边和一条直角边分别相等的两个直角三角形全等.(可以简写成“斜边、直角边”或“HL”)
符号语言表示:在Rt△ABC和Rt△A′B′C′中,
AC=A′C′,
BC=B′C′,
∴△ABC≌△A′B′C′(HL).
注意:用“HL”证明两个直角三角形全等,书写时两个三角形符号前面要加上“Rt”.
C′
直角三角形的专属全等判定方法
新知归纳
已知条件 可选择的判定方法 需寻找的条件
一锐角对应相等
斜边对应相等
一直角边对应相等
直角三角形全等方法大归纳
ASA或AAS
可证直角与已知锐角的夹边对应相等或者与锐角(或直角)的对边对应相等
HL或AAS
可证一直角边对应相等或证一锐角对应相等
HL或ASA或AAS
可证斜边对应相等或证已知边相邻的锐角对应相等或证已知边所对的锐角对应相等
C′
新知练习
判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由:
(1)一个锐角和这个角的对边对应相等; ( )
(2)一个锐角和这个角的邻边对应相等; ( )
(3)一个锐角和斜边对应相等; ( )
(4)两直角边对应相等; ( )
(5)一条直角边和斜边对应相等 ( )
HL
AAS或ASA
SAS
AAS
AAS
判一判
C′
新知典例
例1 如图,AC⊥BC,BD⊥AD,垂足分别为C,D,AC=BD.求证:BC=AD.
证明:∵AC⊥BC,BD⊥AD,
∴∠C与∠D都是直角.
在Rt△ABC和Rt△BAD中,
AB=BA,
AC=BD,
∴Rt△ABC≌Rt△BAD(HL).
∴BC=AD.
课堂练习
变式 如图,AC⊥BC,BD⊥AD,要证△ABC≌△BAD,需要添加一个什么条件?请说明理由.
(1) AD = BC 理由: HL
(2) AC = BD 理由: HL
(3) ∠DBA =∠CAB 理由: AAS
(4) ∠DAB =∠CBA 理由: AAS
新知典例
证明:∵CE=BF,
∴CE-FE=BF-EF,即CF=BE.
在Rt△ABE和Rt△DCF中,
AB=DC,
BE=CF,
∴Rt△ABE≌Rt△DCF(HL).
∴AE=DF.
例2 如图,AB=CD,AE⊥BC,DF⊥BC,垂足分别为E,F,CE=BF.求证:AE=DF.
A
B
C
E
D
F
课堂总结
三角形全等的判定
HL
对比
探究
应用
斜边和一条直角边分别相等的两个直角三角形全等
根据已知条件选择适合证明两个直角三角形全等的方法
利用“HL”解决实际问题
课堂练习
1.如图,BF=CE,AE⊥BC,DF⊥BC,添加一个条件____,即可证明Rt△ABE≌Rt△DCF.下列添加的条件不正确的是( )
A.AB=DC B.AE=BF
C.EA=FD D.∠A=∠D
B
课堂练习
2.下列说法不正确的是( )
A.两条直角边对应相等的两个直角三角形全等
B.一锐角和斜边对应相等的两个直角三角形全等
C.斜边和一直角边对应相等的两个直角三角形全等
D.有两边相等的两个直角三角形全等
D
课堂练习
3.已知:如图,AE⊥BC,DF⊥BC,垂足分别为E,F,AE=DF,AB=DC,则△ ≌△ (HL).
ABE
DCF
证明:∵在△ABE和△DCF中,
AE⊥BC,DF⊥BC,AE=DF,AB=DC,
符合直角三角形全等条件HL,
所以△ABE≌△DCF,
课堂练习
4.如图,正方形网格中,点A,B,C,D均在格点上,则∠ACD+∠BDC= °.
90
解:在Rt△AEC和Rt△DAB中
∴Rt△AEC≌Rt△DAB(HL)
∴∠ACE=∠ABD
∵∠EAC+∠ACE=90°
∴∠EAC+∠ABD=90°
∴∠AFB=90°,即∠CFD=90°
∴∠ACD+∠BDC=90°
课堂练习
5.如图,AB⊥BC、DC⊥BC,垂足分别为B、C,AB=6,BC=8,CD=2,点P为BC边上一动点,当BP= 时,形成的Rt△ABP与Rt△PCD全等.
2
解:当BP=2时,Rt△ABP≌Rt△PCD
∵BC=8,BP=2
∴PC=6
∵AB⊥BC、DC⊥BC
∴∠B=∠C=90°
在△ABP和△PCD中
∴△ABP≌△PCD(SAS)
课堂练习
6.如图,在△ABC中,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,E,F为垂足,AE=CF.求证:∠ACB=90°.
证明:如图,在Rt△ACE和Rt△CBF中,
∴Rt△ACE≌Rt△CBF(HL)
∴∠EAC=∠BCF
∵∠EAC+∠ACE=90°
∴∠ACE+∠BCF=90°
∴∠ACB=180°﹣90°=90°
课堂练习
7.如图在△CDE中,∠DCE=90°,DC=CE,DA⊥AB于A,EB⊥AB于B,试判断AB与AD,BE之间的数量关系,并证明.
解:结论:AB=AD+BE.
证明:∵DA⊥AB于A,EB⊥AB于B
∴∠A=∠B;
∵∠DCE=90°,
∴∠ADC+∠ACD=90°,∠ACD+∠ECB=90°;
∴∠ADC=∠ECB;
又∵DC=CE,
在△ACD和△BEC中,
∴△ACD≌△BEC;
∴AD=BC,AC=BE;
∴AB=AC+CB=BE+AD.
课堂练习
8.如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=5cm,P,Q两点分别在AC上和过点A且垂直AC的射线AM上运动,且PQ=AB.当点P运动到AC上什么位置时,△ABC与△QPA全等?
A
B
C
P
M
Q
解:①当点P运动到AP=BC的位置时,
在Rt△APQ和Rt△CBA中,
PQ=BA,
AP=BC,
∴Rt△APQ≌Rt△CBA(HL).
∴AP=BC=5cm.
课堂练习
解:②当点P运动到AP=AC的位置时,
在Rt△APQ和Rt△CAB中,
PQ=AB,
AP=CA,
∴Rt△APQ≌Rt△CAB(HL).
∴AP=AC=10cm.
综上,当点P运动到使AP=5cm或AP=10cm位置时,
△APQ和△CAB全等.
A
B
C(P)
M
Q
作业布置
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
